福建省东山二中2007届高三第一次适应性测试
数学理科试题
一、选择题(共60分)
1、复数![]() ,则实数a的值是( )
,则实数a的值是( )
A.![]() B.
B.![]() C.
C.![]() D.-
D.-![]()
2、![]() 中,若
中,若![]() ,则
,则![]() 为
( )
为
( )
A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定
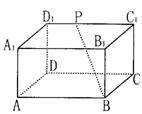 3、如右图,长方体ABCD—A1B1C1D1中,BB1=BC,P为C1D1上一点,则异面直线PB与B1C所成角的大小( )
3、如右图,长方体ABCD—A1B1C1D1中,BB1=BC,P为C1D1上一点,则异面直线PB与B1C所成角的大小( )
A.是45° B.是60°
C.是90° D.随P点的移动而变化
4、设函数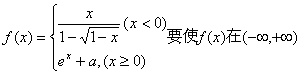 内连续,则实数a值等于( )
内连续,则实数a值等于( )
A.1 B.![]() C.
C.![]() D.
D.![]()
5、关于函数![]() ,有下列命题
,有下列命题
① 其最小正周期为![]() ; ② 其图像由
; ② 其图像由![]() 个单位而得到;
个单位而得到;
③ 其表达式写成![]() ④ 在
④ 在![]() 为单调递增函数;
为单调递增函数;
则其中假命题为( )
A.① B.② C.③ D.④
6、已知![]() 表示平面,m,n表示直线,则m//
表示平面,m,n表示直线,则m//![]() 的一个充分而不必要条件是( )
的一个充分而不必要条件是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7、若函数![]() 内为增函数,则实数a的取值范围( )
内为增函数,则实数a的取值范围( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8、已知双曲线![]() 的左焦点为F1,左、右顶点为A1、A2,P为双曲线上任意一点,则分别以线段PF1,A1A2为直径的两个圆的位置关系为( )
的左焦点为F1,左、右顶点为A1、A2,P为双曲线上任意一点,则分别以线段PF1,A1A2为直径的两个圆的位置关系为( )
A.相交 B.相切 C.相离 D.以上情况都有可能
 9、如图,平面内的两条相交直线
9、如图,平面内的两条相交直线![]() 和
和![]() 将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ (不包括边界). 若
将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ (不包括边界). 若![]() ,且点
,且点![]() 落在第Ⅲ部分,则实数
落在第Ⅲ部分,则实数![]() 满足( )
满足( )
(A) ![]() .
(B)
.
(B) ![]() .
.
(C) ![]() .
(D)
.
(D) ![]() .
.
10、在一次教师联欢会上,到会的女教师比男教师多12人,从这些教师中随机挑选一人表演节目. 若选到男教师的概率为![]() ,则参加联欢会的教师共有( )
,则参加联欢会的教师共有( )
A.120人. B.144人 C.240人 D.360人
11、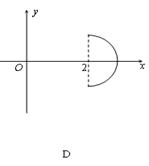
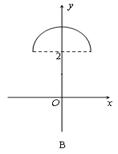
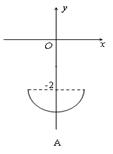
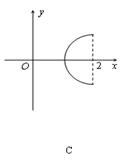 在平面直角坐标系中,已知曲线C:
在平面直角坐标系中,已知曲线C:![]() (θ是参数,且
(θ是参数,且![]() ),那么曲线C关于直线y=x对称的曲线是 ( )
),那么曲线C关于直线y=x对称的曲线是 ( )
12、若不等式![]() 对于任意正整数n恒成立,则实数a的取值范围是( )
对于任意正整数n恒成立,则实数a的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(共16分)
13、已知数列![]() 满足
满足![]() 记
记![]() ,
,
则![]() = .
= .
14、已知函数![]() ,则
,则![]() =
.
=
.
15、已知![]() 则点
则点![]() 所在区域面积是
所在区域面积是
16、点P(3,1)在椭圆![]()
![]()
![]() 的
的![]() 光线经直线y=-2反射后通过椭圆的右焦点,则这个椭椭圆的离心率为
光线经直线y=-2反射后通过椭圆的右焦点,则这个椭椭圆的离心率为
三、解答题(共74分)
17、(本小题12分) 已知函数![]()
(1)当![]() 时,求
时,求![]() 的单调递增区间;
的单调递增区间;
(2)当![]() ,且
,且![]() 时,
时,![]() 的值域是
的值域是![]() ,求a、b的值.
,求a、b的值.
18、(本小题12分)
旅游公司为3个旅游团提供4条旅游线路,每个旅游团任选其中一条.
(1)求3个旅游团选择3条不同的线路的概率
(2)求恰有2条线路没有被选择的概率.
(3)求选择甲线路旅游团数的期望.
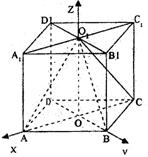
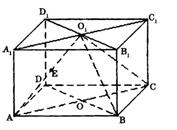
19、(本小题12分) 如图,直四棱柱ABCD—A1B1C1D1的高为3,底面是边长为4且∠DAB=60°的菱形,AC∩BD=0,A1C1∩B1D1=O1,E是O1A的中点.
(1)求二面角O1-BC-D的大小;
(2)求点E到平面O1BC的距离
20、(本小题12分)
在平面直角坐标系中,已知![]() 、
、![]() 、
、![]() ,满足向量
,满足向量
![]() 与向量
与向量![]() 共线,且点
共线,且点![]() 都在斜率为6的同一条直线上.
都在斜率为6的同一条直线上.
(1)试用![]() 与n来表示
与n来表示![]() ;
;
(2)设![]() ,且12<a≤15,求数列
,且12<a≤15,求数列![]() 中的最小值的项.
中的最小值的项.
21、(本小题12分)已知双曲线C的中心在原点,抛物线![]() 的焦点是双曲线C的一个焦点,且双曲线过点(1,
的焦点是双曲线C的一个焦点,且双曲线过点(1, ![]() ).
).
(1)求双曲线的方程;
(2)设直线![]() :
:![]() 与双曲线C交于A、B两点, 试问:
与双曲线C交于A、B两点, 试问:
① ![]() 为何值时
为何值时![]()
② 是否存在实数![]() , 使A、B两点关于直线
, 使A、B两点关于直线![]() 对称(
对称(![]() 为常数), 若存在,
求出
为常数), 若存在,
求出![]() 的值; 若不存在,
请说明理由.
的值; 若不存在,
请说明理由.
22、.(本小题14分) 设函数f(x)=![]() 在[1+,∞
在[1+,∞![]() 上为增函数.
上为增函数.
(1)求正实数a的取值范围.
(2)若a=1,求征:![]()
(n∈N*且n≥2)
参考答案
一、选择题(60分)
BCCA BDAB BAAA
二、填空题(16分)
13、![]()
14、0
15、1
16、![]()
三、解答题(74分)
17、解(1)![]() ,
,
∴递增区间为![]() ----------------------6分
----------------------6分
(2)![]()
而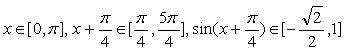 ,
,
故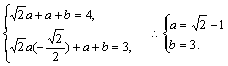 --------------- 12分
--------------- 12分
18、解:(1)3个旅游团选择3条不同线路的概率为:P1=![]() …………3分
…………3分
(2)恰有两条线路没有被选择的概率为:P2=![]() ……6分
……6分
(3)设选择甲线路旅游团数为ξ,则ξ=0,1,2,3
P(ξ=0)=![]() P(ξ=1)=
P(ξ=1)=![]()
P(ξ=2)= ![]() P(ξ=3)=
P(ξ=3)= ![]()
| ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
∴ξ的分布列为:
∴期望Eξ=0×![]() +1×
+1×![]() +2×
+2×![]() +3×
+3×![]() =
=![]() ………………12分
………………12分
19、
|
(1)过O作OF⊥BC于F,连接O1F,
∵OO1⊥面AC,∴BC⊥O1F,
∴∠O1FO是二面角O1-BC-D的平面角,
∵OB=2,∠OBF=60°,∴OF=![]() .
.
在Rt△O1OF在,tan∠O1FO=![]()
∴∠O1FO=60° 即二面角O1—BC—D为60°
(2)在△O1AC中,OE是△O1AC的中位线,∴OE∥O1C
∴OE∥O1BC,∵BC⊥面O1OF,∴面O1BC⊥面O1OF,交线O1F.
过O作OH⊥O1F于H,则OH是点O到面O1BC的距离,
|
解法二:(1)∵OO1⊥平面AC,
∴OO1⊥OA,OO1⊥OB,又OA⊥OB,
建立如图所示的空间直角坐标系(如图)
∵底面ABCD是边长为4,∠DAB=60°的菱形,
∴OA=2![]() ,OB=2,
,OB=2,
则A(2![]() ,0,0),B(0,2,0),C(-2
,0,0),B(0,2,0),C(-2![]() ,0,0),O1(0,0,3)
,0,0),O1(0,0,3)
设平面O1BC的法向量为![]() =(x,y,z),
=(x,y,z),
则![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,
,
∴![]() ,则z=2,则x=-
,则z=2,则x=-![]() ,y=3,
,y=3,
∴![]() =(-
=(-![]() ,3,2),而平面AC的法向量
,3,2),而平面AC的法向量![]() =(0,0,3)
=(0,0,3)
∴cos<![]() ,
,![]() >=
>=![]() ,
,
设O1-BC-D的平面角为α, ∴cosα=![]() ∴α=60°.
∴α=60°.
故二面角O1-BC-D为60°.
(2)设点E到平面O1BC的距离为d,
∵E是O1A的中点,∴![]() =(-
=(-![]() ,0,
,0,![]() ),
),
则d=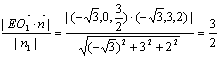 ∴点E到面O1BC的距离等于
∴点E到面O1BC的距离等于![]() 。
。
20、解:(1)![]() 点
点![]() 都在斜率为6的同一条直线上,
都在斜率为6的同一条直线上,
![]()
![]() ,即
,即![]() ,
,
于是数列![]() 是等差数列,故
是等差数列,故![]() .………………3分
.………………3分
![]()
![]() ,
,![]() ,又
,又![]() 与
与![]() 共线,
共线,
![]() …………4分
…………4分
![]()
![]()
![]()
![]() . ………6分
. ………6分
当n=1时,上式也成立.
所以an![]() . ……………7分
. ……………7分
(2)把![]() 代入上式,
代入上式,
得![]()
![]()
![]()
![]() 12<a≤15,
12<a≤15,![]() ,
,
![]() 当n=4时,
当n=4时,![]() 取最小值,
取最小值,![]() 最小值为a4=18-2a. …………12分
最小值为a4=18-2a. …………12分
21、解: (1) 由题意设双曲线方程为![]() ,把(1,
,把(1,![]() )代入得
)代入得![]() (*)
(*)
又![]() 的焦点是(
的焦点是(![]() ,0),故双曲线的
,0),故双曲线的![]() (2分)与(*)
(2分)与(*)
联立,消去![]() 可得
可得![]() ,
,![]() .
.
∴ ![]() ,
,![]() (不合题意舍去)………(3分)
(不合题意舍去)………(3分)
于是![]() ,∴ 双曲线方程为
,∴ 双曲线方程为![]() ………(4分)
………(4分)
(2) 由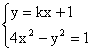 消去
消去![]() 得
得![]() (*),当
(*),当![]()
即![]() (
(![]() )时,
)时,![]() 与C有两个交点A、B ………(5分)
与C有两个交点A、B ………(5分)
① 设A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),因
),因![]() ,故
,故![]() ………(6分)
………(6分)
即![]() ,由(*)知
,由(*)知![]() ,
,![]() ,代入可得
,代入可得
![]() ………(7分)
………(7分)
化简得![]()
∴ ![]() ,检验符合条件,故当
,检验符合条件,故当![]() 时,
时,![]() ………(8分)
………(8分)
② 若存在实数![]() 满足条件,则必须
满足条件,则必须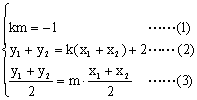 ………(10分)
………(10分)
由(2)、(3)得![]() ………(4)
………(4)
把![]() 代入(4)得
代入(4)得![]() ………(11分)
………(11分)
这与(1)的![]() 矛盾,故不存在实数
矛盾,故不存在实数![]() 满足条件.
………(12分)
满足条件.
………(12分)
22、解:(1)由已知:![]() =
=![]() ………………………2分
………………………2分
依题意得:![]() ≥0对x∈[1,+∞
≥0对x∈[1,+∞![]() 恒成立………………4分
恒成立………………4分
∴ax-1≥0对x∈[1,+∞![]() 恒成立 ∴a-1≥0即:a≥1……5分
恒成立 ∴a-1≥0即:a≥1……5分
(2)∵a=1 ∴由(1)知:f(x)=![]() 在[1,+∞
在[1,+∞![]() 上为增函数,
上为增函数,
∴n≥2时:f(![]() )=
)=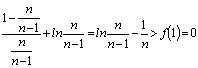
即:![]() …7分
…7分
∴![]() ……………………9分
……………………9分
设g(x)=lnx-x x∈[1,+∞![]() , 则
, 则![]() 对
对![]() 恒成立,
恒成立,
∴g′(x)在[1+∞![]() 为减函数…………12分
为减函数…………12分
∴n≥2时:g(![]() )=ln
)=ln![]() -
-![]() <g(1)=-1<0 即:ln
<g(1)=-1<0 即:ln![]() <
<![]() =1+
=1+![]() (n≥2)
(n≥2)
∴![]()
综上所证:![]() (n∈N*且≥2)成立. ……14分
(n∈N*且≥2)成立. ……14分