上海交通大学附属中学2007-2008学年度第一学期
高三数学期中试卷答题纸
| 一 | 二 | 17 | 18 | 19 | 20 | 21 | 总分 |
一、填空题
1、______3___________ 2、_______
__________
3、______ [2，3）____ 4、_
___（文科：
______
5、____
___；__
___ 6、_
（文科答案：a、b）___
7、_____
________ 8、_____2____________
9、
（文科：
） 10、_.y=1+
(0≤x≤1) ______
11、_____6____________ 12、__①③
②④_______（文科_①②③）
二、选择题
| 题号 | 13 | 14 | 15 | 16 |
| 选项 | A | D | C | B |
三、解答题
17、解：
，∴
…………………（4分）
∴
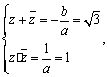
…………………（8分）
（2）∵，∴ 
，∴
，∴
………（16分）
18、解：①f(x)=sin(2x+
)+
[2cos2 (x+
－1)]
=sin (2x+)+cos (2x+)=2cos (2x+－
)…………………（5分）
（或f(x)=2sin(2x++
)）
∴f(x)的最小正周期为
…………………………………………6分
②f(－x)=cos (－2x+－)=cos[2x－(－)]
=cos2xcos (－)+sin2xsin(－)
f(x)=cos(2x+(－)=cos2xcos(－)－sin2xsin(－)………………（9分）
∵f(x)是偶函数，∴f(x)=f(－x)即sin2xsin(－)=0，∴sin(－)=0
∵0≤≤
，－≤－≤
，∴(－)=0，=…………………（12分）
③由f(x)=1得2cos2x=1，∴cos2x=
∵x∈[
，]，∴x=±或x=±………………………………（15分）
所以x的集合是{－，，－，}…………………………（16分）
19、解：（1）∵
∴
…………………（6分）
则-2，是方程
的两实根，∴
…………………（8分）
（2）易知：
，
∵
，∴在
内任意一个x值使
恒成立，……（11分）
由
=
，
…………………（13分）
由
得
得最小值为-4，∴
… …………（16分）
20、解：（1）设
，则由余弦定理
，┅┅┅┅ 4分
即
，解得
， ┅┅┅┅┅┅┅┅┅┅
7分
舍去．所以
.
故佛陈路出口B与花卉世界
之间的距离约为
．┅┅┅┅┅┅┅┅ 8分
（2）在DABD中，由正弦定理得
，┅┅┅┅┅┅┅ 11分
所以
.
在DCBD中，
，
由正弦定理得，
.
┅┅┅┅┅ 14分
花卉大道出口
与花卉世界之间的距离约为．┅┅┅┅┅┅┅ 16分
21、
（I）证明：f(x)+2+f(2a－x)=
=
∴结论成立………………………4分
（Ⅱ）证明：f(x) =
………………………………6分
当a+≤x≤a+1时，－a-1≤-x≤-a-,-1≤a-x≤-,-2≤
则－3≤－1+
≤－2，即f(x)值域为[－3，－2]…………………10分
（Ⅲ）解：g(x)=x2+x+1－a(x≠a)=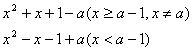 
……13分
（1） 当x≥a－1且x≠a时，g(x)=x2+x+1－a=(x+)2+
如果a－1=－即a≧时，则函数在[a－1,a]和（a,+
）上单调调递增
g(x)min=g(a－1)=(a－1)2
如果a－1<－即a<且a≠－时，g(x)min=g(－)=
－a
当a=－时，g(x)最小值不存在……………………………………15分
（2）当x<a－1时g(x)=x2-x－1+a=(x－)2+a－
如果a－1>即a>时，g（x）min=g()=a－
如果a－1≤即a≤
时g(x)在（－,a－1）上是减函数，g(x)>g(a－1)=
(a－1)2……………………………………………………………………………17分
当a>时(a－1)2－(a－)=（a－）2>0,即（a－1）2>(a—)
当a<且a≠－时，(a－1)2－(－a)=(a－)2>0,即(a－1)2>( －a)……………………………………………………………………………………19分
综合得：
a<且≠－是g(x)最小值是－a
当≤a≤时 g(x)最小值是(a－1)2
当a>时 g(x)最小值为a－
当a=－时 g(x)最小值不存在…………………………………………………20分
文科17、
由
∴
，∴
，∴
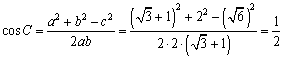或
，又
，∴
∴，