高三数学第一次月考试题
（注意:答案一律写在答题纸上）
一、填空题 (本大题共12小题，每小题4分，共48分)
1. 已知集合A={xx2－px＋15=0}B={xx2－5x＋q=0}，如果A∩B={3}，那么p＋q=
2. 已知集合
，集合
，则
=
3. 设A、B、C是三个集合，则“A∩B=A∩C”是“B=C”的 条件。
4. 已知f (x)＝x5＋ax3＋bx－8，且f (－2)＝10，那么f (2)= 。
5. 设函数 f(x)在 (－∞,+∞)内有定义，下列函数
(1) y=－f(x); (2) y= x f(x2); (3) y=－f(－x); (4) y=f(x)－f(－x)
中必为奇函数的有▁▁▁▁▁▁（要求填写正确答案的序号）。
6．
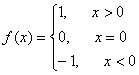，则方程
的各个解之和为
7．已知函数y＝f (x)是奇函数，周期T＝5，若f(－2)＝2a－1则f (7)＝
8．函数 
反函数是
9．某班有50名学生，其中 15人选修A课程，另外35人选修B课程．从班级中任选两名学生,他们是选修不同课程的学生的概率是 (结果用分数表示)．
10．若不等式
的解集为(－1，2)，则实数
=
。
11．当不等式
恰有一个解时，实数
的值是____。
12. 已知集合M＝{x1≤x≤10，x∈N}，对它的非空子集A，将A中每个元素k，都乘以(－1)k再求和(如A={1，3，6}，可求得和为(－1)·1＋(－1)3·3＋(－1)6·6＝2，则对M的所有非空子集，这些和的总和是 ．
二、选择题(本大题共4小题，共16分)
13．若函数y＝f (x) (f (x)不恒为零)的图象与函数y＝－f (x)的图象关于原点对称，则函数y＝f (x) （ ）
（A）是奇函数而不是偶函数 （B）是偶函数而不是奇函数
（C）既是奇函数又是偶函数 （D）既不是奇函数又不是偶函数设函数
14．三人互相传球，由甲开始发球，并作为第一次传球，经过5次传球后，球仍然回到甲手中，则不同的传球方式有 ( )
（A） 6种 （B） 8种 （C） 10种 （D）16种
15、已知关于x的方程：2x=x2解的个数为 （ ）
(A)1 (B)2 (C)3 (D) 4
16. 设函数
的定义域为
，有下列三个命题：
（1）若存在常数
，使得对任意
，有
，则
是函数的最大值；
（2）若存在
，使得对任意，且
，有
，则
是函数的最大值；
（3）若存在，使得对任意，有
，则是函数的最大值.。这些命题中，真命题的个数是 （ ）
（A）0个. （B）1个. （C）2个. （D）3个.
高三数学第一次月考答题纸
一填空
1.________ , 2.______ _, 3._________ , 4._________ _,
5._________ , 6. _________ , 7._________ , 8.________ ,
9.________ _, 10._________ , 11. , 12.
二选择
13._______, 14._______, 15.___ , 16._______,
三、解答题(本大题共6小题，共86分，解答应写出文字说明，证明过程或演算步骤.)
17．（本小题满分12分）
设
是R上的奇函数，
（1）求实数a的值； （2）判定
在R上的单调性.
18. (本小题满分12分)
对定义域分别是
、
的函数
、
，
规定：函数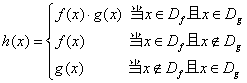
．
（1）若函数
，
，写出函数
的解析式；
（2）求问题（1）中函数的值域；
19. (本小题满分14分)
某城市自来水厂蓄水池现有水9千吨，水厂每小时向池中注水2千吨，
同时向全市供水，x小时内供水总量为8
千吨，问：
(1) 多少小时后，蓄水池内水量最少？
(2) 当蓄水池水量少于3千吨时，供水会出现紧张现象，现决定扩大生产，
每小时向池内注水3千吨，能否消除供水紧张现象，为什么？
20. (本大题满分14分) 已知集合A＝{x êx2＋(a－1)x－a＞0}，B＝{x ê(x＋a)(x＋b)＞0}，其中a≠b，M＝{x êx2－2x－3≤0}，全集I＝R．
(1)若
＝M，求a、b的值；
(2)若a＞b＞－1，求A∩B；
(3)若a2＋
∈
，求a的取值范围．
21.(本小题满分16分)已知二次函数
满足条件：
=
，且方程=
有等根。(1)求的解析式；
(2)是否存在实数m、n(m<n)，使的定义域和值域分别是[m，n]和[3m，3n]?如果存在，求出m、n的值；若不存在，说明理由。
22．(本小题满分18分)
已知函数
的最大值为正实数，集合
，集合
。
（1）求
和
；
（2）定义与的差集：
且
。
设
，
，
均为整数，且
。
为取自
的概率，
为取自
的概率，写出与的二组值，使
，
。
（3）若函数
中，，
是（2）中较大的一组，试写出在区间[
,n]上的最大值函数
的表达式。
参考答案及评分标准
一、填空题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 16 | {1} | 必要 | -26 | ②④ |
| 1-2a |
|
| -4 |
| 2560 |
二、选择题B、C、C、C
三、解答题
17. 解：（1）由
解得a=1…………………………………………6分
（2）由（1）可知
，
在R 上单调递减
单调递增。（或用定义法证明）(略)……………………………………………12分.
18解：（1）= 
………………………………………5分
（2）当
时，
若
其中等号当x=2时成立，…………………………………8分
若x<0
其中等号当x=-2时成立，…………………………………10分
∴函数的值域为
………………………………………12分
19. 设x小时后，蓄水池有水y千吨，………………………………………1分
(1)
y=9＋2x－8
=2(－2)2＋1, 当x=4时,y最小=1…………………8分
即4小时后，水量最少；……………………………………………………9分
(2)
y=9＋3x－8=3(－
)2＋
>3, ……………………………… 12分
即扩大生产后，蓄水池水量最少是千吨，可以消除供水紧张现象。…14分
20． (1)解：A＝{x ê(x－1)(x＋a)＞0}，M＝{x ê－1≤x≤3} ………2分
＝{x｜(x＋a)(x＋b)≤0}
…………3分
若＝M，则a＝1，b＝－3或a＝－3，b＝1．…………………………6分
(2)解：∵a＞b＞－1 ，∴－a＜－b＜1
故A＝
，B＝
x êx＜－a或x＞－b 
………… 8分
因此A∩B＝{x êx＜－a或x＞1}．…………………………………………10分
(3)
＝{x ê(x－1)(x＋a)≤0}，
由a2＋
∈ 得：(a2－
)( a2＋＋a)≤0，…………………………12分
解得：
或
，
∴a的取值范围是{x｜或}．…………………… 14分
21.解: (1)由条件易得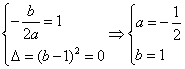
,∴
……7分
(2)假设存在这样的m、n满足条件,由于
所以3n≤即n≤<1,故二次函数f (x)在区间[m,n]上是增函数, 从而有
…………………………16分
22. （1）∵
，配方得
，由
得最大值
。……………………………………………………………3分
∴
，
。…………………………6分
（2）要使
，
。可以使①
中有3个元素，
中有2个元素， 
中有1个元素。则
。…………………………………………………9分
②中有6个元素，中有4个元素， 中有2个元素。则
…………………………………………………………………………12分
（3）由（2）知
…………………………13分
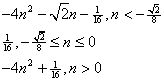………………………………………………18分