高三数学月考试题
一、 选择题（每小题5分，把每小题的正确答案所对应的字母填在题后相应的表格内）
1、若集合
，则M∩N=
A．{3} B．{0} C．{0，2} D．{0，3}
2、不等式
的解集是
A．
B．
C．
D．
3、函数f(x)＝
的定义域是
A．
－∞，0] B．[0，＋∞
C．（－∞，0） D．（－∞，＋∞）
4、设
＝x－1－x，则
A．－
B．0 C． D．
1
5、设
，集合
，则
A．1
B．
C．2
D．
6、已知曲线
的一条切线的斜率为
，则切点的横坐标为
A．1 B．2 C．3 D．4
7、若函数
在区间
内恒有>0，则的单调递增区间为
A．
B．
C．(0,¥) D．
8、对任意实数a，b，c，给出下列命题：
①“
”是“
”充要条件； ②“
是无理数”是“a是无理数”的充要条件③“a>b”是“a2>b2”的充分条件；④“a<5”是“a<3”的必要条件.
其中真命题的个数是
A．1 B．2 C．3 D．4
9、命题：“若
，则
”的逆否命题是
A.若
，则
B.若，则
C.若
，则
D.若，则
10．在
上定义的函数是偶函数，且
，若在区间
是减函数，则函数
A.在区间
上是增函数，区间
上是增函数
B.在区间上是增函数，区间上是减函数
C.在区间上是减函数，区间上是增函数
D.在区间上是减函数，区间上是减函数
11、已知定义域为R的函数在区间
上为减函数，且函数
为偶函数，则
A.
B. 
C. 
D. 
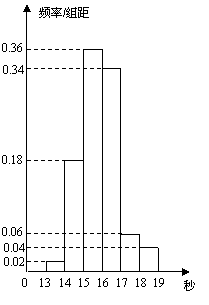12、某班50名学生在一次百米测试中，成绩全部介于13秒与19秒之间，将测试结果按如下方式分成六组：第一组，成绩大于等于13秒且小于14秒；第二组，成绩大于等于14秒且小于15秒；
第六组，成绩大于等于18秒且小于等于19秒．右图是按上述分组方法得到的频率分布直方图．设成绩小于17秒的学生人数占全班总人数的百分比为
，成绩大于等于15秒且小于17秒的学生人数为
，则从频率分布直方图中可分析出和分别为
A．0.9，35 B．0.9，45
C．0.1，35 D．0.1，45
选择题答题表：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
二、填空题（每小题4分）
13、某校有学生2000人，其中高三学生500人．为了解学生的身体素质情况，采用按年级分层抽样的方法，从该校学生中抽取一个200人的样本．则样本中高三学生的人数为___________．
14、已知集合
，
，若
，则实数
的取值范围是
15、把下面不完整的命题补充完整，并使之成为真命题：
若函数
的图象与
的图象关于
对称，则函数=
。（注：填上你认为可以成为真命题的一种情形即可，不必考虑所有可能的情形）.
16．函数
的图象恒过定点A,若点A在直线
上，其中
，则
的最小值为 .
三、解答题 （17-21每题12分，22题14分）
17．用列举法写出集合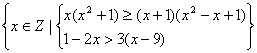
18．求下列函数
的定义域、值域和单调区间．
19、已知p:方程x2＋mx＋1=0有两个不等的负根；q:方程4x2＋4(m－2)x＋1＝0无实根．若“p或q”为真，“p且q”为假，求m的取值范围
20．二次函数f（x）满足
且f（0）=1.
(1) 求f（x）的解析式;
(2) 在区间
上,y= f（x）的图象恒在y=2x+m的图象上方,试确定实数m的范围
21．设函数
为奇函数，其图象在点
处的切线与直线
垂直，导函数
的最小值为
．（1）求，
，
的值；
（2）求函数
的单调递增区间，并求函数在
上的最大值和最小值．
22 
参考答案：
一、选择题 BAADC ADBDB DA
二、填空题 13、 50 14、 （2，3） 15、 如 ①x轴，－3－log2x ②y轴，3+log2(－x) ③原点，－3－log2(x) ④直线y=x, 2x－3 16 8
17. 
18.解析：①原函数的定义域是；②由，得
，
，∴
，∴
，∴原函数的值域是
；
③∵
，
又当
，
从而
；
当
，
从而
．
19.
20．解： (1)设f（x）=ax2+bx+c，由f（0）=1得c=1，故f（x）=ax2+bx+1.
∵f(x+1)-f(x)=2x,∴a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x.
即2ax+a+b=2x,所以
,∴f(x)=x2-x+1.
……………6分
(2)由题意得x2-x+1>2x+m在[-1,1]上恒成立.即x2-3x+1-m>0在[-1,1]上恒成立.
设g(x)= x2-3x+1-m,其图象的对称轴为直线x=,所以g(x) 在[-1,1]上递减.
故只需g(1)>0,即12-3×1+1-m>0,解得m<-1.
21解析：本题考查函数的奇偶性、单调性、二次函数的最值、导数的应用等基础知识，以及推理能力和运算能力．
（Ⅰ）∵为奇函数，∴
即
∴
∵
的最小值为∴
又直线的斜率为
因此，
∴
，，．
（Ⅱ）
．
，列表如下：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极大 |
| 极小 |
|
所以函数的单调增区间是
和
∵
，
，
∴在上的最大值是，最小值是．
22、解析：这是一个含参数a的不等式，一定是二次不等式吗？不一定，故首先对二次项系数a分类：（1）a≠0（2）a=0，对于（2），不等式易解；对于（1），又需再次分类：a>0或a<0，因为这两种情形下，不等式解集形式是不同的；不等式的解是在两根之外，还是在两根之间。而确定这一点之后，又会遇到1与
谁大谁小的问题，因而又需作一次分类讨论。故而解题时，需要作三级分类。
解：
综上所述，得原不等式的解集为：
；
；
欢迎访问 http://www.k12zy.com