盂县一中高三第二次周练(文科)
命题人:岳志义
一、选择题(每题5分,共60分)
1.含有三个实数的集合可表示为{a,![]() ,1},也可表示为{a2, a+b,0},则a2006+b2006
,1},也可表示为{a2, a+b,0},则a2006+b2006
的值为 ( )
A.0 B.1 C.-1 D.±1
2.已知全集I={0,1,2},满足CI(A∪B)={2}的A、B共有的组数为 ( )
A.5 B.7 C.9 D.11
3.设集合M={xx=![]() ,k∈Z},N={xx=
,k∈Z},N={xx=![]() ,k∈Z},则( )
,k∈Z},则( )
A.M=N B.M![]() N C.M
N C.M![]() N D.M∩N=
N D.M∩N=![]()
4.对于任意的两个实数对(a,b)和(c,d),规定(a,b)=(c,d)当且仅当a=c,b=d;运算“![]() ”为:
”为:![]() ,运算“
,运算“![]() ”为:
”为:![]()
![]() ,设
,设![]() ,若
,若![]() 则
则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知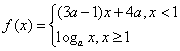 是
是![]() 上的增函数,那么 a 的取值范围是( )
上的增函数,那么 a 的取值范围是( )
A.(0,1) B.(0,![]() ) C.
) C.![]() ,
,![]() D.
D.![]()
6.函数![]() 的定义域( )
的定义域( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知函数![]() ,对任意的两个不相等的实数
,对任意的两个不相等的实数![]() ,都有
,都有![]() 成立,且
成立,且![]() ,
,
则![]() 的值是( )
的值是( )
A.0 B.1 C.2006! D.(2006!)2
8.如图所示,fi(x)(i=1,2,3,4)是定义在[0,1]上的四个函数,其中满足性质:“对[0,1]中任意的x1和x2,任意λ∈[0,1],
f[λx1+(1-λ)x2]≤λf(x1)+(1-λ)f(x2)恒成立”的只有 ( )
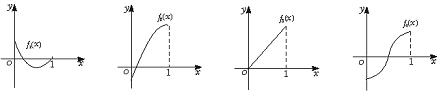
f1(x) f2(x) f3(x) f4(x)
A.f1(x),f3(x) B.f2(x) C.f2(x),f3(x) D.f4(x)
9.不等式x2-x-6>3-x的解集是( )
(A)(3,+∞) (B)(-∞,-3)∪(3,+∞)
(C)(-∞,-3)∪(-1,+∞)
(D)(-∞,-3)∪(-1,3)∪(3,+∞)
10、设![]() ,则
,则![]() 的定义域为
的定义域为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11、若不等式x2+ax+1³0对于一切xÎ(0,![]() 〕成立,则a的取值范围是( )
〕成立,则a的取值范围是( )
A.0
B. –2
C.-![]() D.-3
D.-3
12、若关于![]() 的不等式
的不等式![]() ≤
≤![]() +4的解集是M,则对任意实常数
+4的解集是M,则对任意实常数![]() ,总有( )
,总有( )
(A)2∈M,0∈M;
(B)2![]() M,0
M,0![]() M;
M;
(C)2∈M,0![]() M; (D)2
M; (D)2![]() M,0∈M.
M,0∈M.
二、填空题(每题4分,共16分)
13、函数![]() 对于任意实数
对于任意实数![]() 满足条件
满足条件![]() ,若
,若![]() 则
则![]() __________.
__________.
14、设不等式2x-1>m(x2-1)对满足m≤2的一切实数m的取值都成立,
x的取值范围为
15、设函数y=f(x)是最小正周期为2的偶函数,它在区间[0,1]
上的图象为如图14所示的线段AB,则在区间[1,2]上f(x)
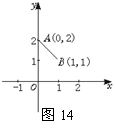 =
.
=
.
16、已知直线![]() 过点
过点![]() ,且与
,且与![]() 轴、
轴、![]() 轴的正半轴分别交于
轴的正半轴分别交于![]() 两点,
两点,![]() 为坐标原点,则三角形
为坐标原点,则三角形![]() 面积的最小值为 .
面积的最小值为 .
三、解答题
17、(12分)已知向量![]() ,
,![]() ,
,![]() ,其中
,其中![]() .
.
(1)当![]() 时,求
时,求![]() 值的集合;
值的集合;
(2)求![]() 的最大值.
的最大值.
18.(12分)设![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
.
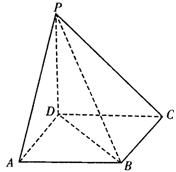
19、(本小题满分12分)
|
(Ⅰ)求证:PD⊥平面ABCD;
(Ⅱ)求二面角A—PB—D的大小.
20.(本小题满分12分)
从4名男生和2名女生中任选3人参加演讲比赛,求:
(Ⅰ)所选3人中恰有1名女生的概率;
(Ⅱ)所选3人中至少有1名女生的概率.
21、(12分)已知函数![]() 在
在![]() 与
与![]() 时都取得极值.
时都取得极值.
(1) 求![]() 、
、![]() 的值及函数
的值及函数![]() 的单调区间;
的单调区间;
(2) 若对![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
22.(14分)已知二次函数![]() .
.
(1)若a>b>c, 且f(1)=0,证明f(x)的图象与x轴有2个交点;
(2)在(1)的条件下,是否存在m∈R,使池f(m)=- a成立时,f(m+3)为正数,若
存在,证明你的结论,若不存在,说明理由;
(3)若对![]() ,方程
,方程![]() 有2个不等实根,
有2个不等实根,![]()
答案
一、1.B;2.C;3.B;4.B 5.C;6.B;7.B; 8.A.9、D 10、B 11、C 12、A
二、13.![]() 14、
14、![]() 15、x 16、4
15、x 16、4
三、17、讲解 (1)由![]() ,得
,得![]() ,即
,即
![]() .
.
则 ![]() , 得
, 得 ![]() .
.
∴ ![]() 为所求.
为所求.
(2)![]()
![]()
![]() ,
,
所以![]() 有最大值为3.
有最大值为3.
18、解:由![]() .
.
∵![]() ,∴
,∴![]() .
.
当![]() ,即
,即![]() 无实根,由
无实根,由![]() ,
,
即![]() ,解得
,解得![]() ;
;
当![]() 时,由根与系数的关系:
时,由根与系数的关系:![]() ;
;
当![]() 时,由根与系数的关系:
时,由根与系数的关系:![]() ;
;
当![]() 时,由根与系数的关系:
时,由根与系数的关系:![]() ;
;
综上所得![]()
19、解答:(Ⅰ)∵PD=CD=1,PC=![]()
∴PD2+CD2=PC2,即PD⊥CD. (3分)
又PD⊥BC.BC∩CD=C ∴PD⊥平面ABCD (6分)
(Ⅱ)如图,连结AC交BD于O,则AC⊥BD.
∵PD⊥平面ABCD,
∴PD⊥AC.
∴AC⊥平面PBD. (8分)
过O点作OE⊥PB于E,连结AE,
则AE⊥PB,故∠AEO为二面角
A—PB—D的平面
角. (10分)
由Rt△OEB∽Rt△PDB,得
OE=![]() .
.
∴tan∠AEO=![]() 即∠AEO=60°
即∠AEO=60°
20、解答:(I)设所选3人中恰有1名女生为事件A,则
![]() 6分
6分
(II)设所选人中至少有1名女生为事件B,则所选3人中没有女生为事件![]() . 8分
. 8分
![]() 10分
10分
![]()
21、解答:
![]()
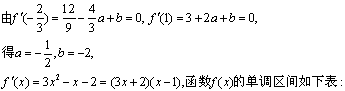
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极大值 |
| 极小值 |
|
所以函数![]() 的递增区间为
的递增区间为![]() 与
与![]() ;递减区间为
;递减区间为![]() .
.

22、
解: (1)![]() 的图象与x轴有两个交点.
的图象与x轴有两个交点.
(2)![]() 的一个根,由韦达定理知另一根为
的一个根,由韦达定理知另一根为
![]()
![]()
![]()
![]()
![]() 在(1,+∞)单调递增,
在(1,+∞)单调递增,![]() ,即存在这样的m使
,即存在这样的m使
![]()
(3)令![]() ,则
,则![]() 是二次函数.
是二次函数.
![]()
![]() 的根必有一个属于
的根必有一个属于![]() .
.