高三数学第二次模拟理

哈尔滨第九中学2007届高三第二次模拟

数学（理）试题

第Ⅰ卷 （选择题　共60分）

一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1．若集合=　　　　　　　　　　　　　（　 ）

　　　 A．　　　　　　　　　　　　　　　　 B．　　

　　　 C．　　　　　　　　　　　　　　　　D．

2．设（i为虚数单位）则　　　　　　　　　　　　　　　　　（　　）

　　　 A．1　　　　　　　　　　　　B．0　　　　　　　　　　　　C．　　　　D．－1．

3．在△ABC中，　　　　　　　　　　　　　　　　　　　　　　（　　）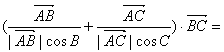

　　　 A．2　　　　　　　B．2　　　　　　　 C．2　　　　　　　 D．0

4．从5位男数学教师和4位女数学教师中选出3位教师派到3个班担任班主任（每班1位

　 班主任）要求这3位班主任中男女教师都有，则不同的选派方案共有　　　　　　　　（　　）

　　　 A．210　　　　　　　　　　 B．420　　　　　　　　　　 C．630　　　　　　　　　　 D．840

5．函数为奇函数，=　　　　　　　　　　（　　）

　　　 A．0　　　　　　　　　　　　B．1　　　　　　　　　　　　C．　　　　　　　　　　　D．5

6．函数平移后，得到函数，则是

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　 B．2　　　　　　　 C．　　　　　　　　 D．2

7．球表面积为20，球面上有A、B、C三点，若AB=AC=2，BC=2则球心到平面ABC

　 距离为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．1　　　　　　　　　　　　B．　　　　　　　　　　C．　　　　　　　　　　D．2

8．若直线的交点在实轴上射影恰好为双曲线的焦

　 点，则双曲线的离心率是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　B．2　　　　　　　　　　　　C．2　　　　　　　　　D．4

9．数列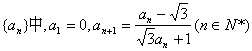，其前n项和S_n，则S₂₀₀₇　　　　　 （　　）

　　　 A．0　　　　　　　　　　　　B．－　　　　　　　　 C．　　　　　　　　　　D．2

2,4,6

10．已知数列的前n项和为S_n，则等于　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．0　　　　　　　　　　　　B．1　　　　　　　　　　　　C．2　　　　　　　　　　　　D．

11．已知向量的夹角为60°，则直线的位置关系是（　　）

　　　 A．相切　　　　　　　　　 B．相交　　　　　　　　　 C．相离　　　　　　　　　 D．随的值而确定

12．已知点图象上的两个不同的点（　　）

　　　 ①　　　　　　　　　　　　　　　　　②

　　　 ③　　　　　　　　　　 ④

　　　 A．1　　　　　　　　　　　　B．2　　　　　　　　　　　　C．3　　　　　　　　　　　　D．4

第Ⅱ卷 （非选择题 共90分）

	2,4,6

二、填空题（本大题共4小题，每小题4分，共16分.把答案填写在横线上）.

13．展开式中x³的系数　　　　　　　　 .

14．已知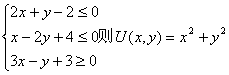取最小值时x+y=　　　　　　  .

15．已知A（2，－1），B（－1，1），0为坐标原点，动点M满足，且则点M的轨迹方程为　　　　　　  .

16．已知的定义域为R，它的反函数互为反函数，

且的值　　　　　　  .

三、解答题（本大题共6小题，共76分，解答应写出文字说明、证明过程或演算步骤）

17．（本小题满分12分）在△ABC中，内角A、B、C对边分别是a、b、c，

已知

　 （1）试判断△ABC的形状；　

　 （2）若求角B的大小.

18．（本小题满分12分）甲有一个箱子，里面放有x个红球,y个白球（）；乙有一个箱子，里面放有2个红球，1个白球，1个黄球.现在甲从箱子任取2个球，乙从箱子里在取1个球，若取出的3个球颜色全不相同，则甲获胜.

　 （1）试问甲如何安排箱子里两种颜色的个数，才能使自己获胜的概率最大？

　 （2）在（1）的条件下，求取出的3个球中红球个数的数学期望.

19．（本小题满分12分）如图，在平行四边形ABCD中，已知AB=CD=a，AD=BC=2a，

∠A=60°AC∩BD=E，将其沿对角线BD折面直二面角

　 （1）证明AB⊥平面BCD

　 （2）求二面角A—CE—B的大小.

20．（本小题满分12分）设函数

　 （1）若上是增函数，求a的取值范围.

　 （2）求上的最大值.

21．（本小题满分12分）设上的两点，满足，椭圆的离心率短轴长为2，0为坐标原点.

　 （1）求椭圆的方程；

　 （2）若直线AB过椭圆的焦点F（0，c），（c为半焦距），求直线AB的斜率k的值；

　 （3）试问：△AOB的面积是否为定值？如果是，请给予证明；如果不是，请说明理由.

22．（本小题满分14分）已知数列

　 （1）求数列的通项公式；

　 （2）若数列证明是等差数列；

　 （3）证明

参考答案

2,4,6

选择题：BADBC　BABAB　CD

填空：－20　　　　　　　　0

17．解：（1）由余弦定理得：

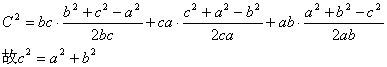
所以△ABC是以角C为直角的直角三角形.

另解：由正弦定理得：

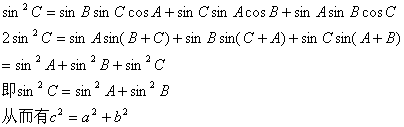
（2）

又

故

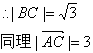
在Rt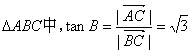

…………………………12分

18．（1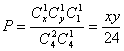）………………………………………………3分

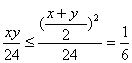
当且仅当x=y=2时“=”成立

所以当红球与白球各2个时甲获胜的概率最大………………………………5分

（2）

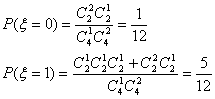
…………10分

所以……………………12分

19．（1）在三角形ABC中由余弦定理，得BD²=AD²+AB²－2ADABcos60°=3a²

∴AD²=4a²=3a²+a²=BD²+AB²　

∴∠ABD=90°…………………………3分

又∵二面角A—BD—C为直二面角，AB平面ABD，平面ABD∩平面BCD=BD

∴AB⊥平面BDC…………………………6分

（2）作BQ⊥CE于点Q，连AQ，

∵AB⊥面BCD

∴BQ为AQ在平面BCE的射影，

AQ⊥CE

∴∠BQA为二面角A—CE—B的平面角……………………………………8分

设折叠前A的位置是A

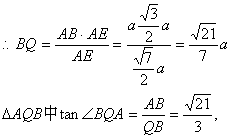
………………………………11分

∴二面角A—CE—B的大小为…………………………12分

20．设函数

因为上是增函数，所以上恒成立；

解得时，时，当且仅当

当不恒成立，

所以上是增函数时，a的取值范围为.

　 （2）当时，上是增函数，所以

当，解得：，且可判断初取得最大值

综上：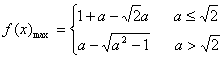

21．（1）

椭圆的方程为　（2分）

　 （2）设AB的方程为

由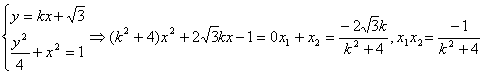

（4分）

由已知

　　2　（7分）

  （3）当A为顶点时，B必为顶点.S_△AOB=1　　 （8分）

当A，B不为顶点时，设AB的方程为y=kx+b

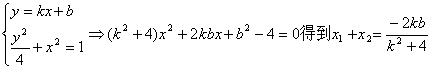
（11分）

所以三角形的面积为定值.（12分）

22．解：（1）

是以a₁+1=2为首项，2为公比的等比数列，

……………………4分

（2）（证法一）

①

②

②－①得

即③

④

④－③得

即

是等差数列.……………………8分

证法二：同证法一得

令n=1得，b_­1­=2，设b­₂=2+d（d∈R）用数学归纳法证明b_­n­=2+（n－1）d

（i）当n=1,2时等式成立；

（ii）假设当n=k（k≥2）时，b_n=2+（n－1）d，那么

即当n=k+1时等式也成立.

由（i）、（ii）或知都成立.

是等差数列.

　 （Ⅲ）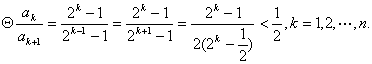

　（10）

.（14分）