2007年漳州市高中毕业班第二次质量检查试卷
数 学(文科)
本试卷分第I卷(选择题)和第II卷(非选择题)两部分. 满分150分,考试用时120分钟.
参 考 公 式:
如果事件A、B互斥,那么 球的表面积公式
P(A+B)=P(A)+P(B) ![]()
如果事件A、B相互独立,那么
P(A·B)=P(A)·P(B) 其中R表示球的半径
如果事件A在一次试验中发生的概率是 球的体积公式
P,那么n次独立重复试验中恰好发生k ![]()
次的概率![]() 其中R表示球的半径
其中R表示球的半径
第Ⅰ卷(选择题,共60分)
一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设全集U={1,3,5,7,9},集合A={1,a-5,9},CUA={5,7},则实数a的值为 ( )
A.0或2 B.2或8 C.3或6 D.1或4
2.已知等差数列![]() 中,
中,![]() 的值是 ( )
的值是 ( )
A.15 B.16 C.17 D.18
3.已知sin(![]() )=
)=![]() ,则cos(
,则cos(![]() )的值为 ( )
)的值为 ( )
A.![]() B.-
B.-![]() C.
C.![]() D.-
D.-![]()
4.已知![]() ,点P满足
,点P满足![]() 等于 ( )
等于 ( )
A.![]() B.
B.![]() C.2 D.1
C.2 D.1
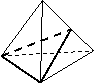 5.正三棱锥底面边长为2,侧棱与底面所成的角为60º,过底面一边作截面,
5.正三棱锥底面边长为2,侧棱与底面所成的角为60º,过底面一边作截面,
使其与底面成30º的二面角,则截面的面积为 ( )
A.3
B.2![]()
C.![]() D.
D.![]()
6.若函数![]() 的反函数
的反函数![]()
![]() ( )
( )
A.1 B.-1 C.1和-1 D.5
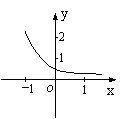 7.函数
7.函数![]() 的图象如图,其中a、b为常数,则下列结论
的图象如图,其中a、b为常数,则下列结论
正确的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8. 函数![]() 为增函数的区间是 ( )
为增函数的区间是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.已知![]() 的两条渐近线所围成的三角形平面区域内(含边界)的任意一点则
的两条渐近线所围成的三角形平面区域内(含边界)的任意一点则![]() 的最大值为( )
的最大值为( )
A.0 B.6-![]() C.7 D.6+
C.7 D.6+![]()
10. 四个朋友要召开一次聚会,每人提出一个日期,其中恰有两人提出的日期是星期六的
概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11. 若不等式x-2-x+2≥a的解集非空,则a的取值范围是( )
A.a≥-4 B.a≤-4 C.a≤4 D.a≥4
12. F1、F2是椭圆C:![]() (a>b>0)的两个焦点,线段F1F2被点(
(a>b>0)的两个焦点,线段F1F2被点(![]() ,0)分成5 :3,则椭圆C的离心率为( )
,0)分成5 :3,则椭圆C的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分,把正确答案填在答题卡中的横线上
13. 二项式(x -![]() )6展开式的中间项为______________________.
)6展开式的中间项为______________________.
14. 平面直角坐标系中有五个点,分别为O(0, 0),A(1, 2),B(2, 4),C(-1, 2),D(-2, 4),过这五个点一共可以作_____________个不同的三角形?
15. 某校高三年级有1200人,在一测试中成绩为A等级的有180人,B等级的有780人,C等级的有240人,采用分层抽样的方法从中抽取一个容量为200的样本,则B等级学生中应抽取_________ 人.
16. 已知三棱锥P—ABC中,PA,PB,PC两两垂直,P,A,B,C四点在同一球面上,且PA=1,PB=2,PC=3,则这个球的表面积是______________.
三、解答题:本大题共6小题,74分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)
已知向量![]() ,
,![]() ,
,
记![]() ,
,![]() 的最小正周期为
的最小正周期为![]() .
.
(1)求![]() 的值;
的值;
(2)叙述![]() 的图象怎样由
的图象怎样由![]() 的图象变化得到.
的图象变化得到.
18. (本小题满分12分)
由于城市人口日益增加,为解决市内交通问题,交管部门每年都要减少摩托车,同时增加公交车,才能有效地解决市内交通问题。设2007年共有燃油型公交车2660辆,计划于2008年投入32辆电力型公交车,随后电力型公交车每年比上一年的投入增加50% ,而不再新增燃油型公交车,试问:
(1)该市在2013年应该投入多少辆电力型公交车?
(2)到哪一年底,电力型公交车的数量开始不少于公交车总数的20%?
19.(本小题满分12分)
一箱商品中共有5件,其中一件有瑕疵,按规则进行有放回的抽检,抽检次数不超过4次,若连续或间隔两次被抽到有瑕疵的那一件则停止检验并退回该箱商品,否则继续抽检直到4次,才决定是否退回该箱商品.
(1)求抽检次数不超过3次的概率;
(2)求该箱商品不被退回的概率.
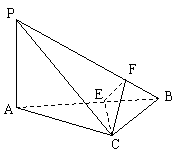 20.(本小题满分12分)
20.(本小题满分12分)
如图,在三棱锥P—ABC中PA=BC=3,
PC=AB=5,AC=4,PB=![]() ,过C作平面CEF⊥PB,
,过C作平面CEF⊥PB,
交AB于E,交PB于F,
(1)求证:PA⊥平面ABC;
(2)求二面角B—CE—F的一个三角函数值;
(3)求异面直线AC与PB所成的角.
21.(本小题满分12分)
设函数![]() 且a为常数)
且a为常数)
(Ⅰ)若函数![]() 在R上单调递增,求实数a的取值范围;
在R上单调递增,求实数a的取值范围;
(Ⅱ)如果![]() 的图象在(-∞,-
的图象在(-∞,-![]() )上递增,在[-
)上递增,在[-![]() ,0]上递减,试求当x∈[0,4]时,
,0]上递减,试求当x∈[0,4]时,![]() 的最大、最小值.
的最大、最小值.
22.(本小题满分14分)
如图,过y轴正半轴上一点M(0,m)的直线与抛物线![]() 交于A、B两点,点A、点B分别在第一、第二象限内,直线
AB的斜率为k(k≠0),点A、B到y轴的距离的差为2k。
交于A、B两点,点A、点B分别在第一、第二象限内,直线
AB的斜率为k(k≠0),点A、B到y轴的距离的差为2k。
(1)求![]() 的值;
的值;
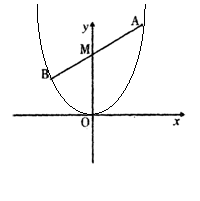 (2)在问题(1)下,当
(2)在问题(1)下,当![]() 时,
时,
求直线AB倾斜角![]() 的取值范围.
的取值范围.
|
2007年漳州市高中毕业班第二次质量检查试卷
数 学(文科)参 考 答 案
一.选择题:每小题5分,共60分.
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答 案 | B | C | B | C | D | B | D | A | D | A | C | B |
二、填空题:13. -160; 14. 8; 15. 130; 16.14π.
三、解答题:
17.解:(1)
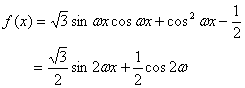
![]() ………………………………………………………………4分
………………………………………………………………4分
∵ T=![]() ,∴
,∴![]() ………………………………………………………6分
………………………………………………………6分
(2)由(1)知![]()
∴只要把![]() 的图象向左平移
的图象向左平移![]() 个单位;再把图象上各点的纵坐标保持不变,横坐标缩小为原来的一半就可得到
个单位;再把图象上各点的纵坐标保持不变,横坐标缩小为原来的一半就可得到![]() 的图象.……………………………………12分
的图象.……………………………………12分
18.解:(1)设2008年为第一年,其电力型公交车数量为a1=32, 第n年电力型公交车的数量为an,依题意{an}为等比数列,a1=32, 公比q=1+50%=![]() ,…………………………3分
,…………………………3分
2013年应该投入 a7=32(![]() )5=243(辆) ……………………………………………6分
)5=243(辆) ……………………………………………6分
(2)记Sn= a1+ a2+ a3+…+ an ,依题意:
![]() ,∴
,∴![]() ……………………………………………………8分
……………………………………………………8分
即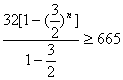 ,解得
,解得![]() , ∴ n≥6 …………………………11分
, ∴ n≥6 …………………………11分
答:到2013年底电力型公交车的数量开始不少于公交车总数的20%. …………12分
19.解:用![]() 表示抽检次数,每一次抽到有瑕疵商品的概率都是p=0.2,则
表示抽检次数,每一次抽到有瑕疵商品的概率都是p=0.2,则
(1)P(![]() ≤3)= P(
≤3)= P(![]() =2)+ P(
=2)+ P(![]() =3)
………………………………………………2分
=3)
………………………………………………2分
= p2+![]() p(1-p)p=0.22+2×0.2×0.8×0.2=0.104 ………………………6分
p(1-p)p=0.22+2×0.2×0.8×0.2=0.104 ………………………6分
(2)若不被退回,就意味着在做完4次抽检时只抽到0次或1次有瑕疵的商品,……8分
其概率为:
(1-p)4+![]() p (1-p)3=0.84+4×0.2×0.8 3=0.8192.……………………………………12分
p (1-p)3=0.84+4×0.2×0.8 3=0.8192.……………………………………12分
20.(1)证:由已知得PC2=PA2+AC2=25,PB2=PA2+AB2=34,
∴PA⊥AC,PA⊥AB,AB∩AC=A, ………………………………………………2分,
∴ PA⊥平面ABC 。…………………………………………………………………4分
(2)∵PA⊥面ABC,∴PA⊥CE,又PB⊥面CEF,∴PB⊥CE,PA∩PB=P,
∴ CE⊥面PAB,∴CE⊥AB,CE⊥EF,
∴∠BEF是二面角B—CE—F的一个平面角,………………………………………6分,
由又PB⊥面CEF知PB⊥EF,
∴ΔPAB∽ΔEFB,∴tan∠BEF=![]() 。…………………………………8分
。…………………………………8分
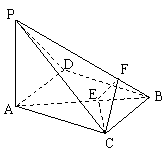 (3)作BD∥CA,连结AD、PD,则∠PBD=AC与PB所成的角,
(3)作BD∥CA,连结AD、PD,则∠PBD=AC与PB所成的角,
BD=4,AD=3,∴AB2=AD2+BD2=25,
∴AD⊥BD,∴PD⊥BD,……………………………10分
∴![]() ,
,
即AC与PB所成的角的大小的余弦值为![]() ……12分
……12分
(2)[解法2]以C为原点,直线CB,CA分别为x、y轴建
立直角坐标系(如图).
则B(3, 0, 0),
A(0, 4, 0), P(0, 4, 3), ![]() ,
,
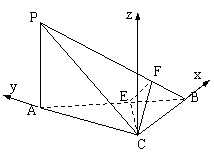
![]() ,
,![]() 分别是平面CEF,平面ABC的法向量,
分别是平面CEF,平面ABC的法向量,
![]() ,
,
∴ 二面角B—CE—F的余弦值为![]() .
.
(3)![]() ,
,![]() ,
,
∴cos<![]() ,
,![]() >=
>=![]() ,
,
∴ 即AC与PB所成的角的大小的余弦值为![]() .
.
21.解:(I)![]() f(x)在R上单增
f(x)在R上单增
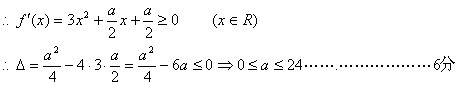
(II)由题意![]() ………………………………8分
………………………………8分
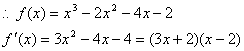
| x | (-∞,- | - | (- | 2 | (2,+ ∞) |
| y′ | + | 0 | - | 0 | + |
| y |
| 极大 |
| 极小 |
|
∴x∈[0,4]时,[0,2]递减[2,4]递增
f (0)=-2 f(2)=-10 f(4)=14
∴f最小(x)=-10 f最大(x)=14 ………………………………………12分
22.(本小题满分14分)
解:(1)设直线AB的方程为![]() 代入抛物线方程得
代入抛物线方程得
![]() ① ……………………………………………………………2分
① ……………………………………………………………2分
设![]() ………………………4分
………………………4分
由于![]()
∴![]() ………………………………………………………………6分
………………………………………………………………6分
(2)∵p=1,所以方程①为:![]()
又![]() ,
,
∴![]()
得![]() ………………………………………………………………9分
………………………………………………………………9分
而 ![]() ,
,
![]() ,两边平方得4k2=m2-12m+4 ……………11分
,两边平方得4k2=m2-12m+4 ……………11分
当![]() 时,
时,![]() ,
,
∴![]() , ∴
, ∴![]()
∴![]() ………………………………………………………………14分
………………………………………………………………14分