2007年漳州市高中毕业班第二次质量检查试卷
数 学（理科）
本试卷分第I卷（选择题）和第II卷（非选择题）两部分. 满分150分，考试用时120分钟。
参考公式：
如果事件A、B互斥，那么 球的表面积公式
P(A+B)=P(A)+P(B)
如果事件A、B相互独立，那么
P(A·B)=P(A)·P(B) 其中R表示球的半径
如果事件A在一次试验中发生的概率是 球的体积公式
P，那么n次独立重复试验中恰好发生k次
次的概率
其中R表示球的半径
第I卷（选择题，共60分）
一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 把正确选项的代号涂在机读卡的相应位置上.
1．设全集U={1，3，5，7，9}，集合A={1，a－5，9}，CUA={5，7}，则实数a的值为 （ ）
A．0或2 B．2或8 C．3或6 D．1或4
2．
等于 （ ）
A．
B．
C．
D．
3．已知sin(
)=
，则cos(
)的值为 （ ）
A． B．-
C．
D． -
4. 四个朋友要召开一次聚会，每人提出一个日期，其中恰有两人提出的日期是星期六的概率为（ ）
A．
B．
C．
D．
5．已知正方体ABCD—A1B1C1D1的棱长为1，对于下列结论，①BD1⊥平面A1DC1；②A1C1和AD1所成角为45°；③点A与点C1在该正方体外接球表面上的球面距离为
，其中正确结论的个数是
（ ）
A．0 B．1
|
6．等差数列{
}的公差为d，前n项和为Sn，当首项a1和d变化时，
是一个定值，则下列各数中也为定值的是（ ）
A．S6 B．S7 C．S13 D．S15
7．
|
的图象如右图，若
则 （ ）
| |
B．
C．
D．以上都不正确
8. 函数
为增函数的区间是 （ ）
A．
B．
C．
D．
9．已知f(x)是偶函数，且在
上为增函数，若f(lgx)> f(1)，则x的取值范围是 (
)
A．(
, 1) B．(0, )∪(10,
+∞) C．(, 10) D．(0, 1)∪(10,
+∞)
10.已知
的最小值为 （ ）
A．6 B．7 C．8 D．9
11．已知数列{}的通项公式上
（
、
为常数），其前
项和为
，若平面上的三个不共线的向量
满足
，且A、B、C三点共线，则S2007=（ ）
A．2007 B．1007 C．
D．
12. 设F1、F2是双曲线C：
(a、b>0)的两个焦点，以F1F2为边作正三角形，这个三角形另两边中点在C上，则双曲线C的离心率为 （ ）
A．
B．
C．
D．
第Ⅱ卷（非选择题 共90分）
二、填空题：本大题共4小题，每小题4分，共16分，把正确答案填在答题卡中的横线上
13.
二项式(x -
)6展开式的中间项为______________________.
14. 平面直角坐标系中有五个点，分别为O(0, 0)，A(1, 2)，B(2, 4)，C(-1, 2)，D(-2, 4)，过这五个点一共可以作_____________个不同的三角形？
15.
，则 a = ，b=
.
16. 由不等式组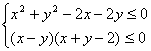
表示的平面区域的面积是________________.
三、解答题：本大题有6小题，共74分. 解答应写出文字说明，证明过程或演算步骤.
17.（本小题满分12分）在ΔABC中，角A、B、C的对边长分别为a、b、c，
且
．
(Ⅰ)求角C；
(Ⅱ)若c=
，求a2+b2的最大值。
18.（本小题满分12分）漳州110某特警训练班共8名队员，某天进行实弹射击比赛，
(Ⅰ)通过抽签将编号为1~8号的8名队员排到1~8号靶位，试求恰有5名队员所抽到靶位号与其编号相同的概率；
(Ⅱ)此次射击比赛规定每人射击3次，总环数不少于29环的队员可获得神枪手称号。已知某队员击中10环和9环的概率均为0.5，
（1）求该队员能获得神枪手称号的概率；
（2）求该队员三次中靶环数总和η的分布列和数学期望。
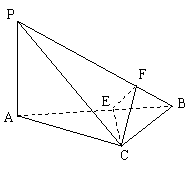19.（本小题满分12分）在三棱锥P—ABC中，PA=BC=3，
PC=AB=5，AC=4，PB=
，
（1）求证：PA⊥平面ABC；
（2）过C作CF⊥PB交PB于F；在线段AB上找一点E，
使得PB⊥平面CEF；
（3）求点A到平面CEF的距离。
20.（本小题满分12分）已知数列{an}满足：a1=3，
，
（1）求证：
是等差数列，并求{an}的通项公式；
（2）求{an}的前n项和Sn。
21．（本小题满分12分）已知动点M到点F
.
（1）求动点M的轨迹C的方程；
（2）若过点E（0，1）的直线与曲线C在y轴左侧交于不同的两点A、B，点P（－2，0）满足
，求直线PN在y轴上的截距d的取值范围.
22．（本小题满分14分）
已知函数
在定义域内连续。
（Ⅰ）求
的单调区间和极值；
（Ⅱ）当m为何值时f（x）≥0恒成立？
（Ⅲ）给出定理：若函数
在[a,b]上连续，并具有单调性，且满足g（a）与g（b）异号，则方程
内有唯一实根。试用上述定理证明：当
且m>1时，方程
内有唯一实根（e为自然对数的底数）。
2007年漳州市高中毕业班第二次质量检查试卷
数 学（理科）参 考 答 案
一．选择题：每小题5分，共60分．
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答 案 | B | B | D | A | C | C | A | A | B | D | C | D |
二、填空题：13. -160； 14. 8； 15. 2，4； 16.π．
三、解答题：
17.（1） 解：由已知得
，
∴
，∴
，
∴C=60°；……………………………………………………………………………………6分
（2）由余弦定理得c2=a2+b2 -2 ab cos60º
∴ a2+b2=c2+2 ab cos60º=2+ab≤2+
∴ a2+b2≤4，当a=b时等号成立，∴a2+b2的最大值为4．………………12分
18.解：（1）记恰有5名队员抽到的靶位与其编号相同的事件为A，则
P(A)=
…………………………………………………^………4分
(2)①记该队员获得神枪手称号的事件为B，则
P(B)=
② P(
=27)=0.53=0.125 , P(=28)=
,
P(=29)= 
, P(=30)= 0.53=0.125
的分布列如下表：
E=27×0.125+28×0.375+29×0.375+30×0.125=28.5
19.（1）证：由已知得PC2=PA2+AC2=25，PB2=PA2+AB2=34，
∴PA⊥AC，PA⊥AB，AB∩AC=A,
∴ PA⊥平面ABC ．……………………………………………………………………4分，
（2）[解法一：] ∵CF⊥PB，只要PB⊥CE，则有PB⊥平面CEF，
又PA⊥平面ABC，∴PA⊥CE，PA∩PB=A，
∴CE⊥平面PAB，∴CE⊥AB， ………………………………………………………6分
设BE=x，ΔACB是RtΔ，∴BC2=BE·AB即9=5x，∴
，
即E点在AB上距B点
． ……………………………………………………………8分
（3）[解法一：]设A到平面CEF的距离为d，由PB2=PC2+BC2=34知PC⊥BC，又PB⊥CF，
∴ΔPBC∽ΔCBF，∴BC2=BF•PB， ∴BF=
，………………10分
同理
，∴
，∴
，∴d=
……12分
（2）[解法二：] 以C为原点，直线CB，CA分别为X、Y轴建立直角坐标系（如图）．
则B(3, 0,
0), A(0, 4, 0), P(0, 4, 3), 
,设E(x，y，0)，则
如解法一分析，只要PB⊥CE，则有PB⊥平面CEF，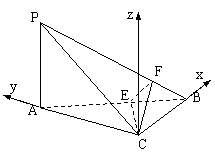
∴
……………………①
又A、E、B三点共线，
，
，
∴
…………………………②
由①②得
，即E（
）
（3）[解法二：] 
，
分别是平面CEF的法向量，
∴A到平面CEF的距离为
。
20. （1）证：由已知得
，
∴ 
，∴{an}是等差数列，公差为1，首项是
，
∴ 
， ∴ 
．
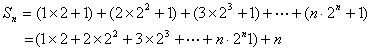
记 
，
则2
，
∴ 
，
∴ 
21．（本小题满分12分）
解：（1）设动点M的坐标为（x，y），由题设可知
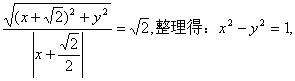
∴动点M的轨迹C方程为
………………………………（4分）
（2）设A（x1，y1），B（x2，y2），由题设直线AB的方程为：
由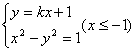
消去y得：
由题意可得：
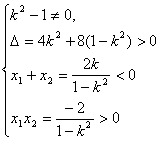解得
………………………………（8分）
则
…………………………………………………………………………………………（10分）
令
上为减函数.
………………（12分）
22．解：（Ⅰ）. 
， ………………………………1分
令
得
,
时，
；
当
，
内是减函数，在
内是增函数，
,
函数
有极小值
. ………………………………5分
（Ⅱ）.由（Ⅰ）知，在定义域
内只有一个极小值点，且在
内是减函数，在内是增函数，
所以，的最小值为，从而当
时，
即实数
的取值范围为
时，不等式
恒成立. ……………………9分
（Ⅲ）
，
又
=
，
，
，
.因此，根据问题中所给的定理，
方程
内有唯一实根. ……………………14分