试卷类型:A
广东省佛山市2007年普通高中高三教学质量检测(二)
数学试题(文科)
本试卷分选择题和非选择题两部分,共4页. 满分150分. 考试时间120分钟.
注意事项:
1.答卷前,考生要务必填写答题卷上的有关项目.
2.选择题每小题选出答案后,用黑色字迹的钢笔或签字笔把答案代号填在答题卷对应的表格内;答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卷各题目指定区域内;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.
4.考生必须保持答题卷的整洁.考试结束后,将答题卷和答题卡交回.
第一部分 选择题(共50分)
一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.设函数![]() 的定义域为A,函数
的定义域为A,函数![]() 的值域为B,则
的值域为B,则![]() ( ).
( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.等差数列![]() 中,
中,![]() ,则
,则![]() ( ).
( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.从一个信箱中任取一封信,记一封信的重量为![]() (单位:克),如果
(单位:克),如果![]() ,
,![]() ,则
,则![]() ( )。
( )。
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知![]() 、
、![]() 满足约束条件
满足约束条件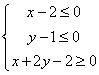 ,则
,则![]() 的取值范围为( )
的取值范围为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知![]() 则
则![]() ( ).
( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.已知![]() 是两个不同平面,
是两个不同平面,![]() 是两条不同直线。给出下列命题:
是两条不同直线。给出下列命题:
①若![]() ∥
∥![]() ②若
②若![]() ∥
∥![]() ∥
∥![]()
 ③若
③若![]() ∥
∥![]() ④若
④若![]() ∥
∥![]()
其中不正确的是( )
A.①② B. ②④ C.①③ D.②③④
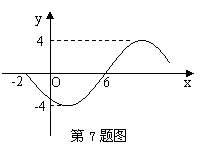
7.函数![]()
部分图象如右图,则函数![]() 的表达式为( )
的表达式为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.设![]() 则( )
则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.过点![]() 的直线与抛物线
的直线与抛物线![]() 交于相异两点
交于相异两点![]() 、
、![]() ,
,![]() 为抛物线顶点,则
为抛物线顶点,则![]()
( )
A. 0 B.1 C.3 D.![]()
10.定义在R上可导的函数![]() ,满足
,满足![]() ,且函数
,且函数![]() 是偶函数,当
是偶函数,当![]() 时,有( )
时,有( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
第二部分 非选择题(共100分)
二、填空题(本大题共5小题,其中11—13题是必做题,14—15题是选做题.每小题5分,满分20分)
11.已知复数![]() ,则
,则![]() _____,
_____,![]() .
.
12.为考察药物A预防B疾病的效果,进行动物试验,得到如下药物效果试验的列联表:
| 患者 | 未患者 | 合计 | |
| 服用药 | 10 | 45 | 55 |
| 没服用药 | 20 | 30 | 50 |
| 合计 | 30 | 75 | 105 |
经计算,随机变量![]() ,请利用下表和独立性检验的思想方法,估计有
,请利用下表和独立性检验的思想方法,估计有
(用百分数表示)的把握认为“药物A与可预防疾病B有关系”。
|
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
|
| 0.46 | 0.71 | 1.32 | 2.07 | 2.71 | 3.84 | 5.024 | 6.635 | 7.879 | 10.828 |
13.如果一个![]() 面体有
面体有![]() 个面是直角三角形,那么我们称这个
个面是直角三角形,那么我们称这个![]() 面体的“直度”为
面体的“直度”为![]() (例如一个五面体共有三个面是直角三角形,我们称这个五面体的“直度”为
(例如一个五面体共有三个面是直角三角形,我们称这个五面体的“直度”为![]() )。那么所有的四面体“直度”的集合为
。
)。那么所有的四面体“直度”的集合为
。
 ▲ 选做题:在下面二道小题中选做一题,二题都选只计算前一题的得分.
▲ 选做题:在下面二道小题中选做一题,二题都选只计算前一题的得分.
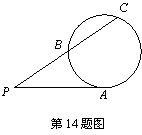
14.如图,圆的切线![]() 的长为
的长为![]() ,
,![]() ,则
,则![]() 的长为
的长为
15.在极坐标系中,过点![]() 且与极轴垂直的直线
且与极轴垂直的直线![]() 的
的
极坐标方程是_______.
三、解答题(本大题共6题,共80分,解答应写出文字说明、证明过程或演算步骤)
16.(本题满分12分)
在三角形ABC中,![]() ,
,![]() 的值和三角形
的值和三角形
 ABC的面积。
ABC的面积。
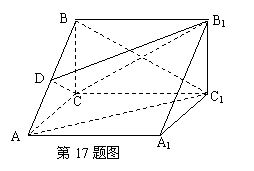
17、(本题满分12分)
如图,在直三棱柱ABC—A1B1C1中,
![]() ,点D是AB的中点。
,点D是AB的中点。
(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() ∥平面
∥平面![]() 。
。
18.(本小题满分14分)
设某旅游景点每天的固定成本为500元,门票每张为30元,变动成本与购票进入旅游景点的人数的算术平方根成正比。
一天购票人数为25时,该旅游景点收支平衡;一天购票人数超过100时,该旅游景点须另交保险费200元。设每天的购票人数为![]() ,盈利额为
,盈利额为![]() 。
。
(Ⅰ)求![]() 与
与![]() 之间的函数关系;
之间的函数关系;
(Ⅱ)试用程序框图描述算法(要求:输入购票人数,输出盈利额);
(Ⅲ)该旅游景点希望在人数达到20人时即不出现亏损,若用提高门票价格的措施,则每张门票至少要多少元(取整数)?
注:(Ⅰ)利润=门票收入—固定成本—变动成本;
(Ⅱ)可选用数据:![]() 。
。
19.(本小题满分14分)
已知函数![]()
![]() 和
和![]() (a、
(a、![]() 为常数)的图象在
为常数)的图象在![]() 处有公共切线.
处有公共切线.
(Ⅰ) 求a的值;
(Ⅱ) 求函数![]() 的极大值和极小值.
的极大值和极小值.
(Ⅲ)若关于![]() 的方程
的方程![]() 有且只有3个不同的实数解,求
有且只有3个不同的实数解,求![]() 的取值范围。
的取值范围。
20.(本小题满分14分)
设A、B分别是直线![]() 上的两个动点,并且
上的两个动点,并且![]() ,动点P满足
,动点P满足![]() 。
。
(Ⅰ)求动点P的轨迹C的方程;
(Ⅱ)若经过点![]() 的直线
的直线![]() 与轨迹C交于不同的两点
与轨迹C交于不同的两点![]() 、
、![]() ,且线段
,且线段![]() 恰被直线
恰被直线![]() 平分,求直线
平分,求直线![]() 的方程。
的方程。
21.(本小题满分14分)
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图. 其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以![]() 表示第
表示第![]() 幅图的蜂巢总数.
幅图的蜂巢总数.
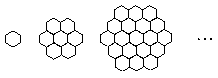
(Ⅰ) 试给出![]() 的值,并求
的值,并求![]() 的表达式(不要求证明);
的表达式(不要求证明);
(Ⅱ) 证明:![]() .
.
广东省佛山市2007年普通高中高三教学质量检测(二)
数学试题参考答案和评分标准(文科)
一、选择题(每题5分,共50分)
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | C | B | C | D | B | C | D | D | D |
二、填空题(每题5分,共20分)
11.![]() ,
,![]() 12.
12.![]() % 13.
% 13.![]() 14.
14.![]() 15.
15.![]()
三、解答题(本大题共6小题,共80分,解答应写出文字说明和演算步骤)
16. 解:由![]() 得
得
![]() ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 5分
┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 5分
(或![]() 或利用移项平方消“元”——化同名函数)
或利用移项平方消“元”——化同名函数)
又在三角形ABC中,![]()
∴![]() 。┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅
7分
。┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅
7分
∴![]() ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅
9分
┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅
9分
![]() 。 ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅12分
。 ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅12分
17.解:(Ⅰ)证明:∵![]() ∴
∴![]() ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅
1分
┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅
1分
又在直三棱柱![]() 中,有
中,有![]() , ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅3分
, ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅3分
∴![]() 平面
平面![]() . ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 5分
. ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 5分
(Ⅱ)证明:设![]() 与
与![]() 交于点P,连结DP。 ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅6分
交于点P,连结DP。 ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅6分
易知P是![]() 的中点,又D是AB的中点。∴
的中点,又D是AB的中点。∴![]() ∥DP。┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅9分
∥DP。┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅9分
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() ∥平面
∥平面![]() . ┅┅┅┅┅┅┅┅┅┅┅┅┅┅12分
. ┅┅┅┅┅┅┅┅┅┅┅┅┅┅12分
18. 解:(Ⅰ)根据题意,当购票人数不多于100时,可设![]() 与
与![]() 之间的函数关系为
之间的函数关系为
![]() 。 ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅2分
。 ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅2分
∵人数为25时,该旅游景点收支平衡,
∴![]() ,解得
,解得![]() ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅———4分
┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅———4分
∴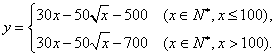 ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅6分
┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅6分
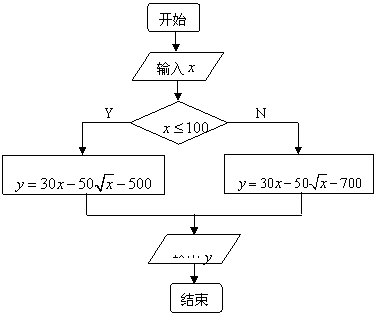 (Ⅱ)框图如下:┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅10分
(Ⅱ)框图如下:┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅10分
(Ⅲ)设 每张门票价格提高为![]() 元,根据题意,得
元,根据题意,得
![]() ------------------------------------------------------11分
------------------------------------------------------11分
∴![]() 。-----------------------------------------------------------------------------------13分
。-----------------------------------------------------------------------------------13分
从而,每张门票最少要37元。-------------------------------------------------------------------------14分
19.解:(Ⅰ)![]() ,
,![]() ,根据题意,得
,根据题意,得![]()
解得![]() . ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 3分
. ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 3分
(Ⅱ)![]() 。
。
令![]() ,得
,得![]() . ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅6分
. ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅6分
∵![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;![]() 时,
时,![]() ,
,![]() 单调递增。∴
单调递增。∴![]() 的极大值为
的极大值为![]() ,
,![]() 的极小值为
的极小值为![]() .┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅
10分
.┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅
10分
(Ⅲ)根据题意,![]() 的图象应与
的图象应与![]() 轴有三个公共点。┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 11分
轴有三个公共点。┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 11分
由(Ⅱ)的结论及![]() 在
在![]() 时
时![]() ,
,![]() 在
在![]() 时
时![]() ,知方程
,知方程![]() 有且只有3个不同的实数解的充要条件为
有且只有3个不同的实数解的充要条件为![]() ┅┅┅┅┅┅┅┅┅┅13分
┅┅┅┅┅┅┅┅┅┅13分
解得![]() ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅
14分
┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅
14分
20.解:(Ⅰ)设![]() ,因为A、B分别为直线
,因为A、B分别为直线![]() 上的点,故可设
上的点,故可设![]() 。∵
。∵![]() ,∴
,∴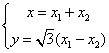
∴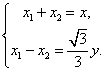 ------------------------------------------------4分
------------------------------------------------4分
又![]() ,∴
,∴![]() 。------------------------5分
。------------------------5分
∴![]() ,即曲线C的方程为
,即曲线C的方程为![]() 。--------------------7分
。--------------------7分
(Ⅱ)因为直线![]() 与直线
与直线![]() 相交,不可能垂直
相交,不可能垂直![]() 轴,
轴,
故可设直线![]() 的方程为:
的方程为:![]() 。--------------------------------8分
。--------------------------------8分
由![]() 消去
消去![]() ,得
,得![]() ,整理得
,整理得
![]() 。---------------------------------------------10分
。---------------------------------------------10分
方程有两个不相等的实数根,![]() ----------------------11分
----------------------11分
∵线段![]() 恰被直线
恰被直线![]() 平分,
平分,
∴![]() 。-----------------------------------12分
。-----------------------------------12分
解得![]() 。∴直线
。∴直线![]() 的方程为
的方程为![]() 。----------------------------14分
。----------------------------14分
(借助于形之间的几何特征进行推导,可相应给分)
21. 解: (Ⅰ) ![]() ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅4分
┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅4分
(Ⅱ)由于![]()
![]()
因此,当![]() 时,有
时,有![]()
所以![]()
![]() .
.
又![]() ,所以
,所以![]() . ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅8分
. ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅8分
(注:直接给出结果也给分)
(Ⅲ)当![]() 时,
时,![]() . ┅┅┅┅┅┅┅┅┅11分
. ┅┅┅┅┅┅┅┅┅11分
所以![]()
![]() . ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅14分
. ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅14分