试卷类型:A
广东省佛山市2007年普通高中高三教学质量检测(二)
数学试题(理科)
本试卷分选择题和非选择题两部分,共4页. 满分150分. 考试时间120分钟.
注意事项:
1.答卷前,考生要务必填写答题卷上的有关项目.
2.选择题每小题选出答案后,用黑色字迹的钢笔或签字笔把答案代号填在答题卷对应的表格内;答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卷各题目指定区域内;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.
4.考生必须保持答题卷的整洁.考试结束后,将答题卷和答题卡交回.
第一部分 选择题(共40分)
一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.设函数![]() 的定义域为A,函数
的定义域为A,函数![]() 的定义域为B,则
的定义域为B,则![]() ( ).
( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.等差数列![]() 中,
中,![]() ,则
,则![]() ( ).
( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知![]() ,则
,则![]() 的值为( ).
的值为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知平面![]() 和两条不同直线
和两条不同直线![]() ,则
,则![]() 的一个必要条件是(
).
的一个必要条件是(
).
A.![]() B.
B.![]()
C.![]() D.
D.![]() 与
与![]() 成等角
成等角
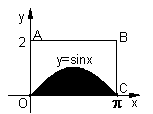 5.如图,在一个长为
5.如图,在一个长为![]() ,宽为2的矩形
,宽为2的矩形![]() 内,曲线
内,曲线![]() 与
与![]() 轴围成如图所示的阴影部分,向矩形
轴围成如图所示的阴影部分,向矩形![]() 内随机投一点(该点落在矩形
内随机投一点(该点落在矩形![]() 内任何一点是等可能的),则所投的点落在阴影部分的概率是( ).
内任何一点是等可能的),则所投的点落在阴影部分的概率是( ).
A.![]() B.
B. ![]()
C. ![]() D.
D.![]()
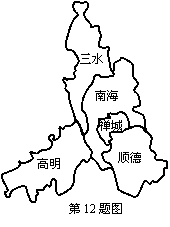
6.2006年1月份开始实施的《个人所得税法》规定:全月总收入不超过![]() 元的免征个人工资、薪金所得税,超过
元的免征个人工资、薪金所得税,超过![]() 元部分需征税.设全月总收入金额为
元部分需征税.设全月总收入金额为![]() 元,前三级税率如下左表所示:
元,前三级税率如下左表所示:
|
|
当工资薪金所得不超过![]() 元,计算个人所得税的一个算法框图如右图. 则输出①、输出②分别为( ).
元,计算个人所得税的一个算法框图如右图. 则输出①、输出②分别为( ).
A.![]() B.
B.![]()
C. ![]() D.
D.![]()
7.已知![]()
![]() (其中
(其中![]() ),当
),当![]() 时,
时,![]() 的值为( ).
的值为( ).
A.正数 B.负数 C.0 D.无法确定
8.定义:复数![]() 是
是![]() (
(![]() 、
、![]() )的转置复数,记为
)的转置复数,记为![]() ;复数
;复数![]() 是
是![]() (
(![]() 、
、![]() )的共轭复数,记为
)的共轭复数,记为![]() .给出下列三个命题:
.给出下列三个命题:
①![]() ; ②
; ② ![]() ; ③
; ③![]() ;
;
其中真命题的个数为( )
A.0 B.1 C.2 D.3
第二部分 非选择题(共110分)
 二、填空题(本大题共7小题,其中9—12题是必做题,13—15题是选做题.每小题5分,满分30分)
二、填空题(本大题共7小题,其中9—12题是必做题,13—15题是选做题.每小题5分,满分30分)
9.已知向量![]() ,且
,且![]() ,则
,则![]() _____.
_____.
10.从装有3个红球,2个白球的袋中随机取出2个球,
以![]() 表示取得红球的个数,则
表示取得红球的个数,则![]() ,
,![]() _____.
_____.
11.已知动点P满足![]() (其中
(其中![]() 、
、
![]() ),当点P的纵坐标是
),当点P的纵坐标是![]() 时,点P到坐标原点的距离是_________.
时,点P到坐标原点的距离是_________.
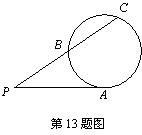
12.假设佛山五区行政区划图如图,测绘局想要给地图着色,要求相邻区域颜色不同.现有4种颜色可供选择,那么共有不同的着色方案为 种.(用数字作答)
 ▲ 选做题:在下面三道小题中选做两题,三题都选只计算前两题的得分.
▲ 选做题:在下面三道小题中选做两题,三题都选只计算前两题的得分.
13.如图,圆的切线![]() 的长为
的长为![]() ,
,![]() ,则
,则![]() 的长为__________.
的长为__________.
14.在极坐标系中,过点![]() 且与极轴垂
且与极轴垂
直的直线![]() 的极坐标方程是_______.
的极坐标方程是_______.
15. 已知![]() 为正数,且满足
为正数,且满足![]() ,则
,则![]() 的最大值是_______________.
的最大值是_______________.
三、解答题(本大题共6题,共80分,解答应写出文字说明、证明过程或演算步骤)
16.(本题满分12分)
已知函数![]() 和
和![]() (a为常数)的图象在
(a为常数)的图象在![]() 处切线平行.
处切线平行.
(Ⅰ) 求a的值;
(Ⅱ) 求函数![]() 的极大值和极小值.
的极大值和极小值.
17、(本题满分12分)
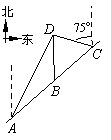 如图,
如图,![]() 是佛山市一环东线的一段,其中
是佛山市一环东线的一段,其中![]() 、
、![]() 、
、![]() 分别是林上路、佛陈路、花卉大道出口,经测量陈村花卉世界
分别是林上路、佛陈路、花卉大道出口,经测量陈村花卉世界![]() 位于点
位于点![]() 的北偏东
的北偏东![]() 方向
方向![]() 处,位于点
处,位于点![]() 的正北方向,位于点
的正北方向,位于点![]() 的北偏西
的北偏西![]() 方向上,并且
方向上,并且![]() .
.
(Ⅰ) 求佛陈路出口![]() 与花卉世界
与花卉世界![]() 之间的距离;(精确到0.1km)
之间的距离;(精确到0.1km)
(Ⅱ) 求花卉大道出口![]() 与花卉世界
与花卉世界![]() 之间的距离.(精确到0.1km)
之间的距离.(精确到0.1km)
![]()
![]() (参考数据:
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() )
)
18.(本小题满分14分)
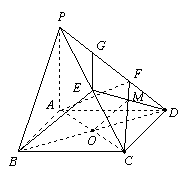
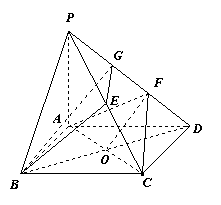
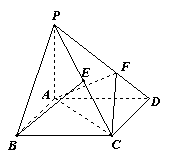 如图,四棱锥
如图,四棱锥![]() 的底面是边长为
的底面是边长为![]() 的正方形,
的正方形,![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,![]() .
.
(Ⅰ) 求证:![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ) 求二面角![]() 的正切值;
的正切值;
(Ⅲ) 求证:![]() 平面
平面![]() .
.
19.(本小题满分14分)
在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]()
![]() ,直线
,直线![]() .
.![]() 、
、![]() 为
为![]() 的两切线,切点为
的两切线,切点为![]() .
.
(Ⅰ) 求证:“若![]() 在
在![]() 上,则
上,则![]() ”是真命题;
”是真命题;
(Ⅱ) 写出(Ⅰ)中命题的逆命题,判断它是真命题还是假命题,并说明理由.
20.(本小题满分14分)
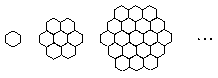
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图. 其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以![]() 表示第
表示第![]() 幅图的蜂巢总数.
幅图的蜂巢总数.
(Ⅰ) 试给出![]() 的值,并求
的值,并求![]() 的表达式(不要求证明);
的表达式(不要求证明);
(Ⅱ) 证明:![]() .
.
21.(本小题满分14分)
已知集合![]() 是满足下列性质的函数
是满足下列性质的函数![]() 的全体:存在非零常数
的全体:存在非零常数![]() ,使得对定义域
,使得对定义域![]() 内的任意两个不同的实数
内的任意两个不同的实数![]() ,均有
,均有![]() 成立.
成立.
(Ⅰ) 当![]() R时,
R时,![]() 是否属于
是否属于![]() ?说明理由;
?说明理由;
(Ⅱ) 当![]() 时,函数
时,函数![]() 属于
属于![]() ,求常数
,求常数![]() 的取值范围;
的取值范围;
(Ⅲ) 现有函数![]() ,是否存在函数
,是否存在函数![]() ,使得下列条件同时成立:
,使得下列条件同时成立:
①函数![]() ;
;
②方程![]() 的根
的根![]() 也是方程
也是方程![]() 的根,且
的根,且![]() ;
;
③方程![]() 在区间
在区间![]() 上有且仅有一解.
上有且仅有一解.
若存在,求出满足条件的![]() 和
和![]() ;若不存在,说明理由.
;若不存在,说明理由.
广东省佛山市2007年普通高中高三教学质量检测(二)
数学试题参考答案和评分标准(理科)
一、选择题(每题5分,共40分)
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | B | C | D | D | A | D | B | C |
二、填空题(每题5分,共30分)
9.![]() 10.
10.![]() ,
,![]() 11.
11.![]() 12.
12.![]() 13.
13.![]() 14.
14.![]() 15.
15. ![]()
三、解答题(本大题共6小题,共80分)
16. 解:(Ⅰ)![]() ,
,![]() ,根据题意,得
,根据题意,得![]()
解得![]() . ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅
4分
. ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅
4分
(Ⅱ)![]() (
(![]() )。
)。
令![]() ,得
,得![]() . ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅
7分
. ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅
7分
∵![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;![]() 时,
时,![]() ,
,![]() 单调递增。 ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 10分
单调递增。 ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 10分
∴![]() 的极大值为
的极大值为![]() ,
,
![]() 的极小值为
的极小值为![]() . ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅
12分
. ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅
12分
17.解:(Ⅰ)设![]() ,则由余弦定理
,则由余弦定理![]() , ┅┅┅┅┅┅┅┅┅┅ 3分
, ┅┅┅┅┅┅┅┅┅┅ 3分
即![]() ,解得
,解得![]() , ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 5分
, ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 5分
![]() 舍去.所以
舍去.所以![]() .
.
故佛陈路出口B与花卉世界![]() 之间的距离约为
之间的距离约为![]() . ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 6分
. ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 6分
(Ⅱ)在DABD中,由正弦定理得![]() , ┅┅┅┅┅┅┅┅┅┅ 8分
, ┅┅┅┅┅┅┅┅┅┅ 8分
所以![]() .
.
在DCBD中,![]() , ┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 10分
, ┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 10分
由正弦定理得,![]() .
.
花卉大道出口![]() 与花卉世界
与花卉世界![]() 之间的距离约为
之间的距离约为![]() . ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 12分
. ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 12分
18. 解:(Ⅰ)∵![]()
![]() ,
,
∴![]() ,即
,即![]() .
┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅2分
.
┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅2分
又![]() ,
,![]() ,
,
∴![]() ⊥平面
⊥平面![]() . ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅4分
. ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅4分
(Ⅱ)方法一:过![]() 作
作![]() 交
交![]() 于
于![]() ,
,
从而![]() 平面
平面![]() ,且
,且![]() ,
,![]() . ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅5分
. ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅5分
过![]() 作
作![]() 交
交![]() 于
于![]() ,由于
,由于![]() ,所以
,所以![]() ,且
,且![]() ,
,
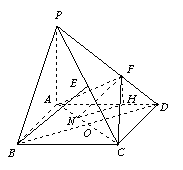
![]() . ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅7分
. ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅7分
连![]() ,根据三垂线定理可得,
,根据三垂线定理可得,![]() ,
,
从而![]() 为二面角
为二面角![]() 的平面角,
的平面角,
不妨设为![]() ,则
,则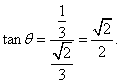
所以二面角![]() 的正切值为
的正切值为![]() .
┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅9分
.
┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅9分
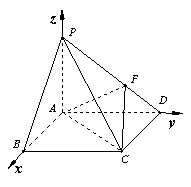
方法二:以![]() 为原点,建立如图所示的坐标系.
为原点,建立如图所示的坐标系.
则![]() .
.
由于![]() ,所以
,所以![]() ,即
,即![]() . ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅5分
. ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅5分
易知![]() 为平面
为平面![]() 的法向量.
的法向量.
设平面![]() 的法向量为
的法向量为![]() ,则
,则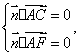 即
即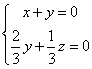 ,
,
令![]() 则
则![]() ,即
,即![]() ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅7分
┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅7分
二面角![]() 的平面角为
的平面角为![]() ,则
,则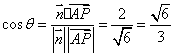 ,所以
,所以![]() ┅┅┅9分
┅┅┅9分
(Ⅲ)方法一:如图,连接![]() ,交
,交![]() 于
于![]() ,取
,取![]() 中点
中点![]() ,连
,连![]() .
.
在△![]() 中,
中,![]() 分别为
分别为![]() 中点,则
中点,则![]() . ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅11分
. ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅11分
在△![]() 中,
中,![]() 分别为
分别为![]() 中点,则
中点,则![]() . ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅12分
. ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅12分
∴平面![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() . ┅┅┅┅┅14分
. ┅┅┅┅┅14分
方法二:如图,连接![]() ,交
,交![]() 于
于![]() ,取
,取![]() 中点
中点![]() ,连
,连![]() 交
交![]() 于
于![]() ,连
,连![]() .
.
在△![]() 中,
中,![]() 分别为
分别为![]() 中点,则
中点,则![]() . ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅10分
. ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅10分
在△![]() 中,
中,![]()
![]() 分别为
分别为![]() 中点,则
中点,则![]() 为
为![]() 中点.
中点.
在△![]() 中,
中,![]() 分别为
分别为![]() 中点,则
中点,则![]() . ┅┅┅┅┅┅┅┅┅┅┅┅┅12分
. ┅┅┅┅┅┅┅┅┅┅┅┅┅12分
 又
又![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() . ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅14分
. ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅14分
方法三、以![]() 为原点,取
为原点,取![]() 为基底,建立空间直角坐标系.
为基底,建立空间直角坐标系.
则![]() ,
,
∴![]()
又E为PC的中点,所以![]() .
.
又![]() ,
,![]()
于是![]() .
.
由平面向量共面定理以及 BE不在平面AFC内可得![]() 平面
平面![]() . ┅┅┅┅┅┅┅┅14分
. ┅┅┅┅┅┅┅┅14分
19.解:(Ⅰ)证明:由![]() 得
得![]() ,对其求导得
,对其求导得![]() . ┅┅┅┅┅┅┅┅┅┅ 2分
. ┅┅┅┅┅┅┅┅┅┅ 2分
设![]() ,则直线
,则直线![]() 的斜率分别为
的斜率分别为![]()
由点斜式得![]() ① ┅┅┅┅┅┅┅┅┅┅┅┅ 4分
① ┅┅┅┅┅┅┅┅┅┅┅┅ 4分
![]() ②, ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 5分
②, ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 5分
由①②可得点![]() ,因为
,因为![]() 在
在![]() 上,所以
上,所以![]() , ┅┅┅┅┅┅┅┅┅ 7分
, ┅┅┅┅┅┅┅┅┅ 7分
所以![]() ,所以
,所以![]() . ┅┅┅┅┅┅┅┅┅┅┅┅ 9分
. ┅┅┅┅┅┅┅┅┅┅┅┅ 9分
(Ⅱ)(Ⅰ)中命题的逆命题为:若![]() ,则
,则![]() 在直线
在直线![]() 上. 为真命题. ┅┅ 11分
上. 为真命题. ┅┅ 11分
事实上,由原命题可知,设![]() ,且
,且
![]() ①
①
![]() ②,
②,
由①②可得点![]() , ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 12分
, ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 12分
又![]() ,
,
所以![]() ,即
,即![]() ,从而点
,从而点![]() 在
在![]() 上. ┅┅┅┅┅ 14分
上. ┅┅┅┅┅ 14分
20. 解: (Ⅰ) ![]() ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅4分
┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅4分
(Ⅱ)由于![]()
![]()
因此,当![]() 时,有
时,有![]()
所以![]()
![]() .
.
又![]() ,所以
,所以![]() . ┅┅┅┅┅┅┅┅┅┅┅┅8分
. ┅┅┅┅┅┅┅┅┅┅┅┅8分
(注:直接给出结果也给分)
(Ⅲ)当![]() 时,
时,![]() . ┅┅┅┅┅11分
. ┅┅┅┅┅11分
所以![]()
![]() . ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅14分
. ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅14分
21.解:(Ⅰ)属于![]() .
.
事实上,对任意![]() ,
,![]() ,故可取常数
,故可取常数![]() 满足题意,因此
满足题意,因此![]() ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅3分
┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅3分
(Ⅱ)![]() 在
在![]() 为增函数
为增函数![]() 对任意
对任意![]() 有
有
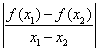
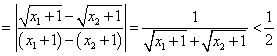 (当
(当![]() 时取到),所以
时取到),所以![]() ,此即为所求.
┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅6分
,此即为所求.
┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅6分
(Ⅲ)存在. 事实上,由(Ⅰ)可知,![]() 属于
属于![]() .
.
![]() 是
是![]() 的根
的根 ![]() ,
,
又![]() . ┅┅┅┅┅┅┅┅┅┅┅┅8分
. ┅┅┅┅┅┅┅┅┅┅┅┅8分
方法一、若![]() 符合题意,则
符合题意,则![]() 也符合题意,故以下仅考虑
也符合题意,故以下仅考虑![]() 的情形。
的情形。
设![]() ,
,
①若![]() ,则
,则
由![]() ,且
,且![]() ,
,
所以,在![]() 中另有一根,矛盾. ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅10分
中另有一根,矛盾. ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅10分
②若![]() ,则
,则![]()
![]() ,
,
所以在![]() 中另有一根,矛盾.
中另有一根,矛盾. ![]() . ┅┅┅┅┅┅┅┅┅┅┅┅┅┅12分
. ┅┅┅┅┅┅┅┅┅┅┅┅┅┅12分
以下证明,对任意![]() 符合题意.
符合题意.
(ⅰ)当![]() 时,由
时,由![]() 图象在连接两点
图象在连接两点![]() 的线段的上方知
的线段的上方知![]()
![]() .
.
(ⅱ)当![]() 时,
时,![]() .
.
(ⅲ)当![]() 时,
时,![]() .
.
从而![]() 有且仅有一个解
有且仅有一个解![]() ,
,![]() 在
在![]() 满足题意.
满足题意.
综上所述:![]() 为所求. ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅14分
为所求. ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅14分
方法二、要使函数![]() 在区间
在区间![]() 有且只有一解,须且只需
有且只有一解,须且只需![]() ,也即
,也即![]() ,也即
,也即![]() 为所求.
为所求.