成都市37中高2007级2006年12月月考数学试题（理科）
1、已知全集
，则
(A) (－1，1)
(B) [－1，1]
（C）
(D)
2、
为虚数单位，复数
等于（ ）
（A）
（B）
（C）
（D）
3、设
，若
存在，则常数b的值是（ ）
（A）0
（B）1
（C）－1
（D）
4、函数
的部分图像是（ ）
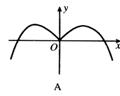
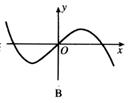
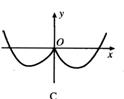
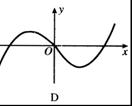
5、在以下的四个式子中，（1）
，（2）
，（3）
，（4）
，不论
是实数，为向量都成立的是（ ）
（A）⑴ ⑵ （B）⑵ ⑶ （C）⑴ ⑷ （D）⑵ ⑷
6、在
中，
（ ）
（A）1 （B）－1 （C）2 （D）－2
7、函数
是奇函数的充要条件是（ ）
（A）
（B）
（C）
（D）
8、关于
的方程
有解，则m的取值范围（ ）
（A）
（B）
（C）
（D）
9、函数
（ ）
（A）周期为
且在
递增 （B）周期为且在
递减
（C）周期为2且在递增 （D）周期为2且在递增
10、若
是R上的减函数，且的图像过点A（0，4）和点B（3，－2），则不等式
的解集为（－1，2）时，
的值为（ ）
（A）0 （B）－1 （C）1 （D）－2
11、已知
，数列
成等差数列，
成等比数列，则下列不等式（1）
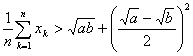，（2）
，（3）
，
（4）
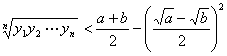，其中成立的有：
（A）⑴ ⑶ （B）⑴ ⑷ （C）⑵ ⑶ （D） ⑵ ⑷
12、从数字1，2，3，4，5中随即抽出3个数字（允许重复），组成一个三位整数，其各位数字之和等于9的概率为（ ）
（A）
（B）
（C）
（D）
二、填空题
13、
的展开式中
的系数为
14、在平行四边形ABCD中，
M为BC中点，则
(用
表示)。
15、
表示不超过的最大整数，（如
），则不等式
的解集为
16、下列命题：①把
的图像向右平移一个单位，再关于
轴对称后得函数
②若
，则函数
是R上的奇函数； ③
的最大值为
；④两个非零向量
，则
的充要条件为
三、解答题
17、已知向量
（1） 若
，求
的值
（2）
设的三边a，b，c满足
，且边b所对应的角
的取值集合为M，当
时，求
的值域。
18、某学校有办公室、教务处、教科处、德育处、后勤处、招生就业处6个处室。各处室主任借助校园网开展有关工作，每个主任上网的概率都是0.5（相互独立）。
（1） 求至少三个主任同时上网的概率；
（2） 至少几个主任同时上网的概率小于0.3
19、数列
中，
（1）
求数列的通项公式；
（2）
设
；
（3）
设
是否存在最大的整数m，使得对任意的
,均有
成立，若存在，求出m的值，若不存在说明理由。
20、经过长期观测得到：在交通繁忙的时段内，某公路段汽车的车流量（千辆/小时）与汽车的平均速度
（千米/小时）之间的函数关系为：
（1）
在该时段内，当汽车的平均速度为多少时，车流量最大，最大车流量是多少？（精确到0.1千辆/小时）
（2） 若要求在该时段内车流量超过10千辆/小时，则汽车的平均速度应在什么范围内？
21、把函数
的图像按向量
平移后得到函数
的图像。
（1）
若
（2）
若不等式
时，
都成立，求实数m的取值范围。
22、已知函数的定义在R上的恒不为零的函数，且对于任意的
都满足
（1）
求
的值，并证明对任意的
都有
；
（2）
设当
，证明在R上是减函数；
（3）设
,表示数列的前n项和，在（2）的条件下，求集合
中的最大元素M与最小的元素m的和。
欢迎访问 http://www.k12zy.com