高三数学《直线与园的方程练习》答案详解

高三《直线与园的方程练习答案》

1．选C　　中，前者位x=0或x²+y²=0表示直线或园；后者表示x=0且x²+y²－4=0，即点（0，2）和（0，-2）两点。

2．答案：B　 解析：直线y=x绕原点逆时针旋转90⁰所得的直线方程为：y=-x.已知圆的圆心（，1）到y=x的距离d=1，又因圆的半径r=1，故相切。

3．选C 园（x＋2）²+y²=1，y/x表示园上点与原点连线的斜率，故切线斜率为其范围。

4．选A 因K_om=b/a，k_g= -a/b,k_l= -a/b.所以g//l,园心到直线L之距为r2/

5．选D 将问题转化成园x²+y²=4上半部分与直线y=k(x-2)+3相交和相切的时候的k值而解

6．答案：B　解析：圆心坐标为（0，0），半径为1.因为直线和圆相切.利用点到直线距离公式得：d==1，即a²+b²=c².所以，以a，b，c为边的三角形是直角三角形.

7．答案：C 解析：圆2x²＋2y²＝1的圆心为原点（0，0）半径r为，圆心到直线xsinθ＋y－1＝0的距离为：∵θ∈R，θ≠＋kπ，k∈Z。∴0≤sin²θ＜1　∴d＞　∴d＞r　∴圆2x²＋2y²＝1与直线xsinθ＋y－1＝0（θ∈R，θ≠＋kπ，k∈Z）的位置关系是相离．

8．答案：A 解析：由已知得点A（－1，0）、P（2，3）、B（5，0），可得直线PB的方程是x+y－5=0.

9．答案：B　解析：∵点（x，y）关于x=y对称的点为(y，x),可知x²y＋xy²＝1的曲线关于x=y对称

10．、B 。可以看成是可行域里的点与点距离的平方加1，故选B.

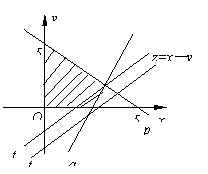11．B  如图 所表示区域为阴影部分的所有整点(横坐标，纵坐标均为整数)，对于直线t： ，即  ，即为直线的纵截距的相反数，当直线位于阴影部分最右端的整点时，

纵截距最小，最大，当 ，时取最大值，，

∴ 　，　又 （4 ，1） ，　

但 (4 ，1) ，　即　

∴ 　　即　

12．作出集合P表示的平面区域，易知为使C_UP恒成立，必须且只需r≤原点O到直线3x+4y-12=0的距离.

13．-1/5<a<1　14.  2 　15. k≤-3/4 或k≥2　　16.　(-12/5, 13/10)

解答题见复印卷子