2008届高三第一学期第二次月考数学试题 、
(文理合卷)时量:120分钟 2007、10、
班次 姓名 记分
一、选择题:(每小题5分共50分)
1.设集合M={1,2},N={2,3},集合P![]() (M∪N),则P的个数是 ( )
(M∪N),则P的个数是 ( )
A. 6 ; B. 8 ; C. 7 ; D. 5 .
2、函数![]() 的图象( )
的图象( )
A.关于![]() 轴对称 B.关于
轴对称 B.关于![]() 轴对称 C.关于原点对称
D.关于直线
轴对称 C.关于原点对称
D.关于直线![]() 对称
对称
3. (文科)在等差数列{![]() }中,
}中,![]() =45,
=45,![]() = ( )
= ( )
A.22 B.20 C.18 D.13
(理科)等比数列{an}中,已知对任意正整数n,a1+a2+a3+…+an=2n-1,则a12+a22+a32+…+an2等于
( )
A、(2n-1)2 B、![]() (2n-1) C、4n-1
D、
(2n-1) C、4n-1
D、![]() (4n-1)
(4n-1)
4、函数![]() (
(![]() )的值域是( )
)的值域是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知![]() 、
、![]() 是非零向量且满足
是非零向量且满足![]() ,
,![]() ,则
,则![]() 与
与![]() 的夹角是( )
的夹角是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6. (文科) 为了得到函数![]() 的图象,可以将函数
的图象,可以将函数![]() 的图象 ( )
的图象 ( )
A.向左平移![]() 个单位长度 B.向右平移
个单位长度 B.向右平移![]() 个单位长度
个单位长度
C.向右平移![]() 个单位长度 D.向左平移
个单位长度 D.向左平移![]() 个单位长度
个单位长度
(理科)若![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
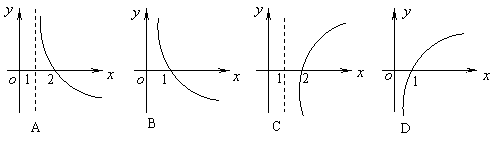 7、函数
7、函数![]() (
(![]() )的反函数的图象大致是( )
)的反函数的图象大致是( )
8.列函数既是奇函数,又在区间![]() 上单调递减的是
( )
上单调递减的是
( )
A.![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
9、若函数![]() 与函数
与函数![]() 在区间
在区间![]() 上的单调性相同,则
上的单调性相同,则![]() 的一个值是( )
的一个值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.定义域为R的函数![]() ,若关于
,若关于![]() 的方程
的方程![]()
恰有5个不同的实数解![]() ,则
,则![]() 等于 ( )
等于 ( )
A.0 B.2lg2 C.3lg2 D.l
二、填空题:(每小题4分共20分)
11、已知:A={ x x-1< 2 },B ={x -1 < x < m + 1},若x∈B成立的一个充分不必要条件是x∈A ,则实数m的取值范围 .
12、已知ΔABC中,∠C=900,
![]() ,
, ![]() =4,则向量
=4,则向量![]() 在向量
在向量![]() 上的投影为
.
上的投影为
.
13、已知函数![]() ,若
,若![]() 为奇函数,则
为奇函数,则![]()
14.(文科) .当![]() 时,函数
时,函数![]() 的最小值为
的最小值为
(理科)定义运算![]() 为:
为:![]() 例如,
例如,![]() ,则函数f(x)=
,则函数f(x)=![]() 的值域为
的值域为
.
15、已知函数![]() 的反函数的图象经过点
的反函数的图象经过点![]() ,那么
,那么![]() 的值等于
的值等于
三、解答题:(本大题共6 个小题共80分)
16.(本小题满分12分)
已知a=1,b=![]() , (1)若a//b,求a·b; (2)若a,b的夹角为135°,求a+b.
, (1)若a//b,求a·b; (2)若a,b的夹角为135°,求a+b.
17、(本小题满分12分)设![]() ,
,![]() ,若
,若![]() ,求实数
,求实数![]() 的取值范围
的取值范围
18、(本小题满分14分)设函数![]() 的图象与直线
的图象与直线![]()
相切于点![]()
(Ⅰ)求![]() 、
、![]() 的值. (Ⅱ)讨论函数
的值. (Ⅱ)讨论函数![]() 的单调性
的单调性
19.(文科)(本小题满分14分)已知:![]() 为常数)
为常数)
(1)若![]() ,求
,求![]() 的最小正周期;
的最小正周期;
(2)若![]() 在[
在[![]() 上最大值与最小值之和为3,求
上最大值与最小值之和为3,求![]() 的值;
的值;
(3求在(2)条件下![]() 的单调减区间
的单调减区间
(理科)
(1) 已知![]() . 若
. 若![]() 且f(x)为偶函数,求
且f(x)为偶函数,求![]() 的值;
的值;
(2):求![]() -4cos10°值;
-4cos10°值;
20、(本小题满分14分)某租赁公司拥有汽车100辆,当每辆车的月租金为3000元,可全部租出,当每辆车的月租金增加50元时,未租出的车将会增加一辆,租出的车每辆每月需要维护费150
元,未租出的车每辆每月需要维护费50元
(Ⅰ)当每辆车的月租金定为3600元时,能租出多少辆车?
(Ⅱ)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大收益是多少?
21.(本小题满分14分)
(文科)(本小题满分14分)已知函数:![]()
(Ⅰ)证明:f(x)+2+f(2a-x)=0对定义域内的所有x都成立.
(Ⅱ)当f(x)的定义域为[a+![]() ,a+1]时,求证:f(x)的值域为[-3,-2];
,a+1]时,求证:f(x)的值域为[-3,-2];
(Ⅲ)设函数g(x)=x2+(x-a)f(x) , 当![]() 求g(x) 的最小值 .
求g(x) 的最小值 .
(理科)已知二次函数![]() (
(![]()
![]() R,
R,![]()
![]() 0).
0).
(I)当0<![]() <
<![]() 时,
时,![]() (
(![]()
![]() R)的最大值为
R)的最大值为![]() ,求
,求![]() 的最小值.
的最小值.
(II)如果![]() [0,1]时,总有
[0,1]时,总有![]()
![]() .试求
.试求![]() 的取值范围.
的取值范围.
(III)令![]() ,当
,当![]() 时,
时,![]() 的所有整数值的个数为
的所有整数值的个数为![]() ,求证数列
,求证数列![]() 的前
的前![]() 项的和
项的和![]()
长沙市实验中学2008届高三第一学期
第二次月考文理科数学试题答案
一、选择题:
C B D C A C A C D C
二、填空题:
11、![]() 12、 -
4 ;13、
12、 -
4 ;13、![]() 14、(文)
14、(文) ![]() (理)[-1,
(理)[-1,![]() ] 15、2
] 15、2
三、解答题:
16.解(1)![]() ,
,
①若![]() ,
,![]() 同向,则
同向,则![]() ……3分
……3分
②若![]() ,
,![]() 异向,则
异向,则![]() ……6分
……6分
(2)![]() 的夹角为135°,
的夹角为135°,![]() ……8分
……8分
![]() ……10分
……10分
![]() ……12分
……12分
17.解:![]() ,
,![]() ………………3分
………………3分
若![]() ,则
,则![]() ……………………4分
……………………4分
(1)若![]() ,即
,即![]() 或
或![]() ,则
,则![]() ,满足
,满足![]() ; …………6分
; …………6分
(2)若![]() ,即
,即![]() 或
或![]() ,则
,则![]() ,若有
,若有![]()
则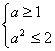 所以
所以![]() ………………9分
………………9分
(3)若![]() ,即
,即![]() ,则
,则![]() ,若有
,若有![]()
则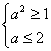 所以
所以![]() ……………………11分
……………………11分
综上所述,![]() 的取值范围为
的取值范围为![]() 或
或![]() ……………………12分
……………………12分
18、解:(Ⅰ)∵![]()
由已知可知![]()
![]()
![]() ①
①
又![]() ②
②
由①②可求得![]() ,
,![]()
(Ⅱ)由(Ⅰ)可知![]()
![]() 或
或![]()
![]()
∴![]() 在
在![]() 和
和![]() 上为增函数
上为增函数
![]() 在
在![]() 上为减函数
上为减函数
19.解:![]() ……2分
……2分
(1)最小正周期![]() ……4分
……4分
(2)![]() ……6分
……6分
![]() …8分
…8分
即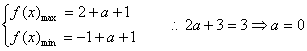 ……10分
……10分
(3)![]()
当 ![]() ,……12分
,……12分
即![]() 时,
时, ![]() 为增函数……14分
为增函数……14分
(理科)(1)解:![]()
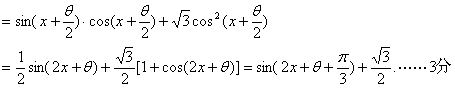
∵f(x)为偶函数。 ∴f(-x)≡f(x)
即![]()
得![]() …………5分
…………5分
∴![]()
又![]() ∴
∴![]() .
…………7分
.
…………7分
(2)解:cot10°-4cos10°=![]() -4cos10°=
-4cos10°=![]()
=![]() …………10分
…………10分
=![]() =
=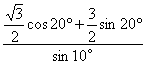 …………12分
…………12分
=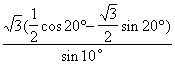 =
=![]() =
=![]() …………14分
…………14分
20、解: (Ⅰ)![]()
能租出100-12=88辆
(Ⅱ)设月收益为![]() 元,租金定为
元,租金定为![]() 元,则有
元,则有![]() 辆租出,
辆租出,
![]() =
=![]()
=![]()
=![]()
∴![]() ∴当
∴当![]() 时
时 ![]() 元
元
答:略
21. (文科)(Ⅰ)证明:![]()
![]()
∴结论成立 ……………………………………4分
(Ⅱ)证明:![]()
当![]()
![]() 即
即![]() …………9分
…………9分
(Ⅲ)解:![]() ,
,![]() …………10分
…………10分
(1)当![]()
则函数在![]() 上单调递增,
上单调递增,![]() ………………………11分
………………………11分
(2)当![]()
![]() …………13分
…………13分
综合得:当![]() 时 g(x)最小值是0 …………14分
时 g(x)最小值是0 …………14分
(理科)解:⑴由![]() 知
知![]() 故当
故当![]() 时
时![]() 取得最大值为
取得最大值为![]() ,…………2分
,…………2分
即![]() ,所以
,所以![]() 的最小值为
的最小值为![]() ;……4分
;……4分
⑵由![]() 得
得![]()
![]() 对于任意
对于任意![]() 恒成立,
恒成立,
当![]() 时,
时,![]() 使
使![]() 成立;…………6分
成立;…………6分
|
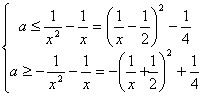 对于任意的
对于任意的![]() ,则
,则![]() ,故要使①式成立,则有
,故要使①式成立,则有![]() ,又
,又![]() ;又
;又![]() ,则有
,则有![]() ,综上所述:
,综上所述:![]() ; …………9分
; …………9分
⑶当![]() 时,
时,![]() ,则此二次函数的对称轴为
,则此二次函数的对称轴为![]() ,开口向上,故
,开口向上,故![]() 在
在![]() 上为单调递增函数,且当
上为单调递增函数,且当![]() 时,
时,![]() 均为整数,故
均为整数,故![]() ,则数列
,则数列![]() 的通项公式为
的通项公式为![]() ,…………12分
,…………12分
故![]() ①,又
①,又![]() ②, 由①—②得
②, 由①—②得
![]() ,
,![]() 。…………14分
。…………14分