湖南省长沙县2007年高三5月三模考试试卷
理科数学(无答案,部分答案可参见文科试卷)
一、选择题:(![]() )
)
1、定义运算![]() ,则符合条件
,则符合条件![]() (
(![]() 为虚数单位)的复数
为虚数单位)的复数![]() 为( )
为( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
2、设![]() 为两个平面,
为两个平面,![]() 为两条直线,且
为两条直线,且![]() ,有如下两个命题:①若
,有如下两个命题:①若![]() ,则
,则![]() ;②若
;②若![]() ,则
,则![]() ,那么( )
,那么( )
A ①是真命题 ②是假命题 B ①是假命题,②是真命题
C ①、②都是真命题 D ①、②都是假命题
3、在![]() 中,
中,![]() 是第3项为-4,第7项为4的等差数列的公差,
是第3项为-4,第7项为4的等差数列的公差,![]() 是第3项为
是第3项为![]() ,第6项为9的等比数列的公比,则
,第6项为9的等比数列的公比,则![]() 是( )
是( )
A 等腰三角形 B 锐角三角形 C 直角三角形 D钝角三角形
4、一植物园参观路径如右图所示,若要全部参观并且路线不重复,则不同的参观路线种数共有( )

A 48种 B 36种
C 12种 D 6种
5、直线![]() 与椭圆
与椭圆![]() 相交与A,B两点,点P在C上,
相交与A,B两点,点P在C上,![]() 的面积等于3,这样的点P共有( )
的面积等于3,这样的点P共有( )
A 1个 B 2个 C 3个 D 4个
6、若两个函数的图象经过若干次平依后能够重合,则称这两个函数为“同形”函数,给出下列三个函数:![]()
![]() ,
,![]() 则( )
则( )
A ![]() 为“同形”函数
为“同形”函数
B ![]() 为“同形”函数,且它们与
为“同形”函数,且它们与![]() 不为“同形”函数
不为“同形”函数
C ![]() 为“同形”函数,且它们与
为“同形”函数,且它们与![]() 不为“同形”函数
不为“同形”函数
D ![]() 为“同形”函数,且它们与
为“同形”函数,且它们与![]() 不为“同形”函数
不为“同形”函数
7、已知函数![]() 的反函数
的反函数![]() 的图象的对称中心是
的图象的对称中心是![]() ,则不等式
,则不等式![]() 的解集是( )
的解集是( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
8、棱长为![]() 的正方体,过从每一个顶点引出的三条棱的中点作一个平面切去正方体的一个角,依次切去各角后所剩多面体的表面积为( )
的正方体,过从每一个顶点引出的三条棱的中点作一个平面切去正方体的一个角,依次切去各角后所剩多面体的表面积为( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
9、如图,圆弧型声波DFE从坐标原点O向外传播,若D是DFE弧与![]() 轴的交点,设
轴的交点,设![]() ,
,![]() ,圆弧型声波DFE在传播过程中扫过平行四边形OABC的面积为
,圆弧型声波DFE在传播过程中扫过平行四边形OABC的面积为![]() (图中阴影部分),则函数
(图中阴影部分),则函数![]() 的图象大致是( )
的图象大致是( )
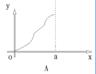

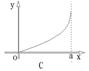
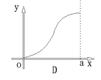
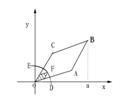
10、已知函数![]()
![]() ,若实数
,若实数![]() 使得
使得![]() 有实根,则
有实根,则![]() 的最小值为( )
的最小值为( )
A ![]() B
B ![]() C 1
D 2
C 1
D 2
二、填空题![]()
11、如果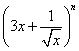 的展开式中各项系数之和为1024,则
的展开式中各项系数之和为1024,则![]() =_______
=_______
12、设数列![]() 满足
满足![]()
![]() ,且
,且![]() ,
,
求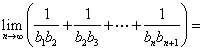 ________
________
13、若![]() ,则
,则![]() ________
________
14、定义![]() ,设实数
,设实数![]() ,满足约束条件
,满足约束条件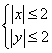 ,
,![]() ,则
,则![]() 的取值范围是________
的取值范围是________
15、已知![]() 与
与![]() 都是定义在R上的函数,
都是定义在R上的函数,![]() ,
,![]() ,
,![]() ,
,![]() ,有穷数列
,有穷数列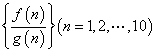 中,任意取前
中,任意取前![]() 项相加,则前
项相加,则前![]() 项和大于
项和大于![]() 的概率等于________
的概率等于________
三、解答题
16、(12分)设函数![]()
⑴求![]() 最小正周期T;
最小正周期T;
⑵求![]() 单调递增区间;
单调递增区间;
⑶设点![]() 在函数
在函数![]() 的图象上,且满足条件
的图象上,且满足条件![]() ,求
,求![]() 的值。
的值。
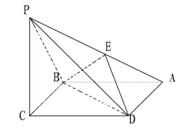 17、(12分)已知四棱锥P-ABCD的底面是边长为
17、(12分)已知四棱锥P-ABCD的底面是边长为![]() 的菱形,
的菱形,![]() ,又
,又![]() ,
,![]() ,E是PA的中点;
,E是PA的中点;
⑴求证:![]() ;
;
⑵求直线PB与直线DE所成的角的余弦值;
⑶设二面角![]() 的平面角为
的平面角为![]() ,求
,求![]() 的值。
的值。
18、(12分)2006年12月9日,在第十五届多哈亚运会羽毛球男子单打决赛中,排名世界第一的林丹迎战陶菲克,在此前一周内,林丹曾两次击败陶菲克,但在决赛中,林丹却意外地以0:2失利,与冠军擦肩而过,根据两人在以往的交战成绩分析,林丹在每一局的比赛中获胜的概率但是0.7,比赛按“三局二胜制”的规则进行(即先胜两局的选手获胜,比赛结束),且设各局之间互不影响;
⑴求林丹以0:2失利的概率;
⑵若林丹与陶菲克下次在比赛中再次相遇,请你计算林丹获胜的概率;
⑶若林丹与陶菲克下次在比赛中再次相遇,试求林丹的净胜局数的分布列和期望值。
19、某地位于沙漠边缘地区,人与自然进行长期顽强的斗争,到2006年底,全区的绿化率已达到30%,从2007年开始,每年将出现以下的变化:原有沙漠面积的16%将栽上树,改造成绿洲,同时原有绿洲面积的4%又被侵蚀变为沙漠。
⑴设全地区面积为1,2006年底绿洲面积为![]() ,经过1年(指2007年底),绿洲面积为
,经过1年(指2007年底),绿洲面积为![]() ,经过
,经过![]() 年绿洲面积为
年绿洲面积为![]() ,求证数列
,求证数列![]() 是等比数列;
是等比数列;
⑵问至少经过多少年的努力,才能使全地区的绿洲面积超过60%。(年取整数)
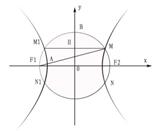 20、(13分)如图
20、(13分)如图![]() 为双曲线E的两焦点,以
为双曲线E的两焦点,以![]() 为直径的圆O与双曲线E交于
为直径的圆O与双曲线E交于![]() ,B是圆O与
,B是圆O与![]() 轴的交点,连接
轴的交点,连接![]() 与OB交于H,且H是OB的中点,
与OB交于H,且H是OB的中点,
⑴当![]() 时,求双曲线E的方程;(4分)
时,求双曲线E的方程;(4分)
⑵试证:对任意的正实数![]() ,双曲线E的离心率为常数;(4分)
,双曲线E的离心率为常数;(4分)
⑶连接![]() 与双曲线E交与点A,是否存在常数
与双曲线E交与点A,是否存在常数![]() ,使
,使![]() 恒成立,若存在试求出
恒成立,若存在试求出![]() 的值,若不存在,请说明理由。(5分)
的值,若不存在,请说明理由。(5分)
21(14分)设函数![]() ;
;
⑴求![]() 的单调区间;
的单调区间;
⑵若当![]() 时,(其中
时,(其中![]() )不等式
)不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
⑶若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上恰好有两个相异的实根,求实数
上恰好有两个相异的实根,求实数![]() 的取值范围。
的取值范围。