高三年级八校联考数学（文）试题

陕西省西安市2007年高三年级八校联考

数学试题（文）

命题人：西工大附中　许德刚

审题人：西安铁一中　刘康宁

注意事项：

1．本试卷分第I卷和第II卷。第I卷为选择题，第II卷为非选择题。

2．考生领到试卷后，须按规定在试卷上填写姓名、准考证号、并在答题卡上填涂对应

　 的试卷类型信息点。

3．所有答案必须在答题卡上指定区域内作答。考试结束后，将本试卷和答题卡一并交

　 回。

第Ⅰ卷（选择题　共60分）

参考公式：

如果事件A、B互斥，那么　　　　　　 P(A+B)=P(A)+P(B)

如果事件A、B相互独立，那么　　　　 P(A·B)=P(A)·P(B)

如果事件A在一次试验中发生的概率是P，那么n次独立重复试验中恰好发生k次的概率　　　　 

球的表面积公式　　　其中R表示球的半径

球的体积公式　　　　 其中R表示球的半径

一、选择题（本大题共12小题，每小题5分，共60分.每小题给出的四个选项中，只有一项是符合题目要求的）

1．若sin2α<0，且tanα·cosα<0，则角α在　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．第一象限　　　　　　B．第二象限　　　　　　C．第三象限　　　　　　D．第四象限

2．设p和q是两个简单命题，若p是q的充分不必要条件，则q是p的　　　　　 （　　）

　　　 A．充分不必要条件　　　　　　　　　　　　　　　　 B．必要不充分条件

　　　 C．充要条件　　　　　　　　　　　　　　　　　　　　　 D．既不充分也不必要条件

3．设M为非空的数集M　　 {1，2，3}，且M中至少含有一个奇数元素，则这样的集合M

　 共有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．6个　　　　　　　　　　B．5个　　　　　　　　　　C．4个　　　　　　　　　　D．3个

4．如图1所示，正三棱柱ABC—A₁B₁C₁的底面边长为2，

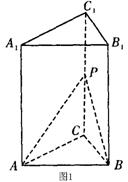
　 高为4，过底面的边AB作一截面交侧棱CC₁于P点，

　 且截面与底面成60°角，则截面△PAB的面积是（　　）

　　　 A．　　　　　　　　 B．

　　　 C．　　　　　　　　　D．

5．若的展开式的第5项是常数项，则正整数n的值

　 为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．12　　　　　　　　　　　B．13　　　　　　　　　　　 C．14　　　　　　　　　　　D．15

6．某学习小组共8名同学，其中男生6人女生2人.现从中抽取3名男生1名女生参加某项

　 活动，则不同的抽取方法共有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．240种　　　　　　　　B．80种　　　　　　　　　C．70种　　　　　　　　　D．40种

7．设P为△ABC所在平面内一点，且满足，则P是△ABC

　 的　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．重心　　　　　　　　　 B．垂心　　　　　　　　　 C．外心　　　　　　　　　 D．内心

8．已知实数x、y满足取得的最小值为－6，则常数m的值为

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．－2　　　　　　　　　　 B．0　　　　　　　　　　　　C．2　　　　　　　　　　　　D．5

9．已知m、n为两条不同的直线，α、β为两个不同的平面，若m⊥α,n⊥β，则下列命题

　 不正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．若m//n，则α⊥β　　　　　　　　　　　　　　 B．若α⊥β，则m⊥n

　　　 C．若m、n相交，则α、β相交　　　　　　 D．若α、β相交，则m、n相交

10．已知函数f(x)=a^x(a>0，且a≠1)，若f^－1(2)<0，则函数y=f^－1(x+1)的图象中可能是（　　）

11．若椭圆的左、右焦点分别为F₁、F₂，线段F₁F₂被抛物线y²=2bx的焦点F分成3：1两段，则此椭圆的离心率为　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A． 　　　　　　　　　　B．　　　　　　　　　 C．　　　　　　　　　　　D．

12．设a=sin15°+cos15°，b=sin17°+cos17°，则下列各式正确的是　　　　　　　　　 （　　）

　　　 A．a<<b 　　　　　　　　　　　　　　　　　B．b<<a

　　　 C．a<b< 　　　　　　　　　　　　　　　　　D．b<a<

第Ⅱ卷（非选择题　共90分）

二、填空题（本大题共4小题，每小题4分，共16分.把答案填在题中横线上）

13．棱长为a的正方体的内切球的体积为　　　　　   .

14．已知圆C：x²+y²－2x+4y=0，则过原点O且与圆C相切的直线方程为　 　　　　  .

15．设函数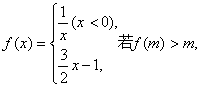则实数m的取值范围是　　　　　　　   .

　　 用区间形式表示）

16．黑、白两种颜色的正六边形地砖按如图2所示产的规律拼成若干个图案：

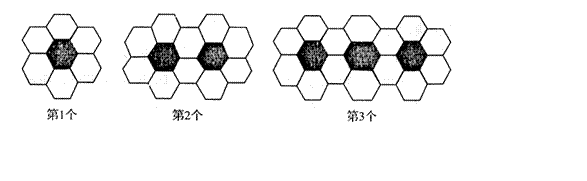　　则第n个图案中有白色地砖　　　　   块.

三、解答题（本大题共6小题，共74分.解答应写出文字说明、推理过程或演算步骤）

17．（本小题满分12分）

已知的值.

18．（本小题满分12分）

　　从4名男生和2名女生中任选3人参加演讲比赛，求：

　 （Ⅰ）所选3人中恰有1名女生的概率；

　 （Ⅱ）所选3人中至少有1名女生的概率.

19．（本小题满分12分）

在数列{a­_n}中，a₁=2，a₂=3，且{a_n·a­_n+1}(n∈N*)是以3为公比的等比数列，记b_n=a_2n－1+a_2n

(n∈N*).

　 （Ⅰ）分别求a₃、a₄、a₅、a₆的值；

　 （Ⅱ）求证：{b_n}是等比数列.

20．（本小题满分12分）

如图3，四棱锥P—ABCD的底面边长为1的正方形，PD⊥BC，且PD=1，PC=.

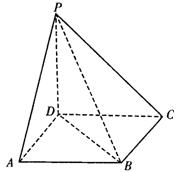
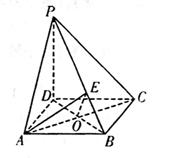
　 （Ⅰ）求证：PD⊥平面ABCD；

　 （Ⅱ）求二面角A—PB—D的大小.

21．（本小题满分12分）

　　　　已知函数，在曲线y=f(x)的所有切线中，有且仅有一条切线l与直线2x+y=0平行.

　 （Ⅰ）求a的值及切线l的方程；

　 （Ⅱ）求函数f(x)的极大值和极小值.

22．（本小题满分14分）

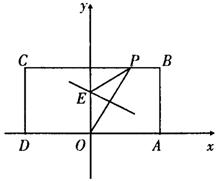
　　　　如图4，在矩形ABCD中，已知A（2，0）、C（－2，2），点P在BC边上移动，线段OP的垂直平分线交y轴于点E，点M满足

　 （Ⅰ）求点PM的轨迹方程；

　 （Ⅱ）已知点F（0，），过点F的直线l交点

M的轨迹于Q、R两点，且求实数的取值范围.

陕西省西安市2007年高三年级八校联考

数学试题（文）参考答案

一、选择题（每小题5分，共60分）

1.D　　2.A　　3.B　　4.C　　5.A　　6.D　　7.B　　8.B　　9.D　　10.A

11.B　 12.C

二、填空题（每小题4分，共16分）

　 13． 　 14. 　 15.(－∞，－1)∪（2，+∞）　 16.4n+2

三、解答题（共74分）

17．，

.　　　　  ②

，　　　　  ①

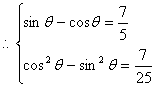　　　　　　　　　　　　　　　　　　　　　　　　　　　 3分

将①代入②，得.③　　　　　　　　　　　　　　　　　 5分

由①、③得　 ③　　　　　　　　　　　　　　　　 7分

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　9分

故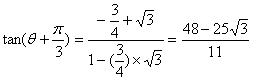　　　　　　　　　　　　　　12分

18．（I）设所选3人中恰有1名女生为事件A，则

　　　　　　　　　　　　　　　　　　　　　 6分

　 （II）设所选人中至少有1名女生为事件B，则所选3人中没有女生为事件. 8分

　　　　 　　　　　　　　　　　　　　　　　　　　　　　　10分

　　  　　　　　　　　　　　　　　　　　　　　　　　　　　　12分

19．（I）∵{a_n·a_n+1}是公比为3的等比数列，

∴a_n·a_n+1=a₁a₂·3^n－1=2·3ⁿ

∴

　　　　　　　　　　　　　　　　　　6分

（II）∵{a­_na_n+1}是公比为3的等比数列，

　　  ∴a_na_n+1=3a_n－1a_n，即a_n+1=3a_n－1　　　　　　　　　　　　　　　　　　　3分

∴a₁，a₃，a₅，…，a_2n－1，…与a₂，a₄，a₆，…，a_2n，…都是公比为3的等比数列.

∴a_2n－1=2·3^n－1，a_2n=3·3^n－1　　　　　　　　　　　　　　　　　　　 10分

∴bn=a_2n－1+a_2n=5·3^n－1

故{b_n}是首项为5，公比为3的等比数列.　　　　　　　　　　　12分

20．（Ⅰ）∵PD=CD=1，PC=

∴PD²+CD²=PC²，即PD⊥CD. 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（3分）

又PD⊥BC.BC∩CD=C　  ∴PD⊥平面ABCD　　　　　　　　　　　　　　　　　　　　　 （6分）

　 （Ⅱ）如图，连结AC交BD于O，则AC⊥BD.

∵PD⊥平面ABCD，

∴PD⊥AC.

∴AC⊥平面PBD. 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（8分）

过O点作OE⊥PB于E，连结AE，

则AE⊥PB，故∠AEO为二面角

A—PB—D的平面

角. 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（10分）

由Rt△OEB∽Rt△PDB，得

OE=.

∴tan∠AEO=即∠AEO=60°　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （12分）

21．（I）∵切线l与直线 2x+y=0平行，

∴f′(x)=ax²+4x+2=－2，即ax²+4x+4=0.　　　　　　　　　　　　　　　　　　　　　　　　 2分

又这样的切线l仅有一条，

∴△16－16=0,得a=1.

　　　　将a=1代入ax²+4x+4=0，得x=－2.

从而y=,即切点坐标为（－2，）.

故：y－=2(x+2)，即6x－3y+16=0.　　　　　　　　　　　　　　　　6分

　 （II）f′(x)=x²+4x+2

由f′(x)>0，得x<－2－或x>－2+.

　　　　 ∴函数f(x)在（－∞，－2－和[－2+，+∞上单调增，在[－2－，

－2+]上单调递减.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 9分

故f(x)_极大=f(－2－)=(1+)；

f(x)_极小=f(－2+)=(1－).　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 12分

22．（I）依题意，设P（t,2）（－2≤t≤2），M（x，y）.

　　　　当t=0时，点M与点E重合，则M=（0，1）；　　　　　　　　　　　　　　　　　　　　1分

　　　　当t≠0时，线段OP的垂直平分线方程为

　　　　 

　　　　

　　　　 显然，点（0，1）适合上式 。

　　　　 故点M的轨迹方程为x²=－4(y－1)( －2≤x≤2).　　　　　　7分

　 （II）设得

　　　　 x²+4k－2=0.

　　　　 设Q（x₁,y₁）、R（x₂,y₂），则

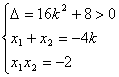　　　　　　　　　　　　　　　　　　　　　　　　　　　　　8分

，　　　　　　　　　　　　　　　　　　　　　　 10分

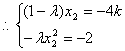
消去x₂，得.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　12分

解得.