陕西省西安市2007年高三年级八校联考
数学试题（理）
命题人：西工大附中 许德刚
审题人：西安铁一中 刘康宁
注意事项：
1．本试卷分为第Ⅰ卷和第Ⅱ卷。第Ⅰ卷为选择题，第Ⅱ卷为非选择题。
2．考生须到试卷后，须按规定在试卷上填写姓名、准考证号，并在答卡上填涂对应的
试卷类型和信息点。
3．所有答案必须在答题卡上指定区域内作答。考试结束后，将本试卷和答题卡一并交
回。
第Ⅰ卷（选择题 共60分）
参考公式：
如果事件A、B互斥，那么P（A+B）=P（A）+P（B）
如果事件A、B相互独立，那么 P（A·B）=P（A）·P（B）
如果事件A在一次试验中发生的概率是P，那么n次独立重复试验中恰好发生k次的概率
球的表面积公式
，其中R表示球的半径
球的体积公式
，其中R表示球的半径
一、选择题（本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的）
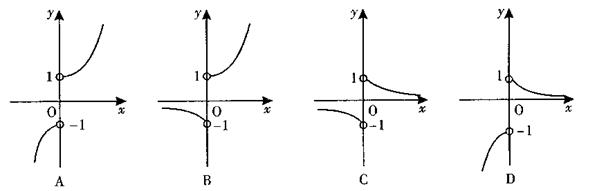
1．设U为全集，M、P是U的两个子集，且
等于 （ ）
A．M B．P C．CUP D．○
2．若复数
为纯虚数，其中
，i为虚数单位，则
的值为
（ ）
A．－1 B．－i C．1 D．i
3．在空间中，设m、n为两条不同的直线，α、β为两个不同的平面，则m⊥α的一个充分
条件是 （ ）
A．α⊥β且m
β B．α⊥β且m//β
C．α//β且m⊥β D．m⊥n且n//α
| |
与圆
关于直线l对称，则
直线l的方程为 （ ）
A．x－y=0 B．x+y=0
C．x－y+6=0 D．x+y－6=0
5．设O为平行四边形ABCD的对称中心，
等于 （ ）
A．
B．
C．
D．
6．某小组共有8名同学，其中男生6人，女生2人，现从中按性别分层随机抽4个参加一
项公益活动，则不同的抽取方法共有 （ ）
A．40种 B．70种 C．80种 D．240种
|
的图象的大致形状是 （ ）
8．若
的展开式中只有第6项的系数最大，则该展开式中的常数项为
（ ）
A．462 B．252 C．210 D．10
9．若点P（a,3）到直线4x－3y+1=0的距离为4，且点P在不等式2x+y－3<0表示的平面区域内，则a的值为 （ ）
A．－3 B．3 C．7 D．－7
|
的侧面ABB1A1内有一动点P到直
线AA1和BC的距离相等，则动点
P的轨迹是 （ ）
A．线段
B．椭圆的一部分
C．双曲线的一部分
D．抛物线的一部分
11．在△ABC中，tanA是第3项为－4、第7项
为4的等差数列的 公差，tanB是第3项为
，
第6项为9的等比数列的公比，则△ABC是 （ ）
A．等腰三角形 B．锐角三角形
C．直角三角形 D．钝角三角形
12．设函数
，给出下列四个命题
①若c=0，则f（x）为奇函数；
②若b=0，c>0，则方程f（x）=0只有一个实根；
③函数y= f（x）的图象关于点（O，C）成中心对称图形；
④关于x的方程f（x）=0最多有两个实根.
其中正确的命题是 （ ）
A．①、③ B．①、④ C．①、②、③ D．①、②、④
第Ⅱ卷（非选择题 共90分）
二、填空题（本大题共4小题，每小题4分，共16分。把答案填在题中的横线上）
13．函数
的最小正周期是
.
|
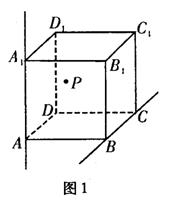
平面ABC上.若正三棱锥A—ABC的底面边
| |
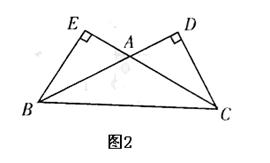
15．如图2，在△ABC中，∠ABC=∠ACB=30°，
AB、AC边上的高分别为CD、BE，则以B、
C为焦点，且经过D、E两点的椭圆与双曲
线的离心率之和为 .
16．在直角坐标平面内，已知点到P1（1、2），P2（2，22），P3（3，23），…，Pn（n,2n），…如果n为正整数，则向量
的坐标为
.（用n表示）
三、解答题（本大题共6小题，共74分，解答应写出文字说明、推理过程或演算步骤）
17．（本小题满分12分）在直角坐标平面内，已知三点A（3，0）、B（3，0）、C（cos
，sin），其中
（Ⅰ）若
求角的弧度数；
（Ⅱ）若
的值.
18．（本小题满分12分）袋中装有大小相等的3个白球、2个红球和n和黑球，现从中任取2个球，每取得一个白球得1分，每取得一个红球得2分，每取得一个黑球得0分，用
表示所得分数，已知得0分的概率为
：
（Ⅰ）袋中黑球的个数n；
（Ⅱ）的概率分布列及数学期望E.
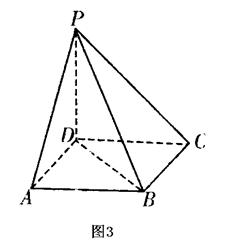
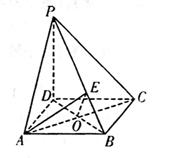
19．（本小题满分12分）如图3，四棱锥P—ABCD的底面是边长为1的正方形，PD⊥BC，
PD=1，PC=
.
|
（Ⅱ）求二面角A—PB—D的大小.
20．（本小题满分12分）设函数
.
（Ⅰ）求函数f（x）的单调区间和极值；
（Ⅱ）若对任意的
不等式 f′（x）≤a恒成立，求a的取值范围.
21．（本小题满分12分）设双曲线的中心在原点，焦点在x轴上，实轴长为2，它的两条渐近线与以A（0，1）为圆心、
为半径的圆相切。直线l过点A且与双曲线的左支交于B、C两点.
（Ⅰ）求双曲线的方程.
（Ⅱ）若
求直线l的方程；
22．（本小题满分14分）已知曲线C：
的横坐标分别为1和
，且a1=5，数列{xn}满足xn+1=tf（xn－1）+1（t>0）,且（
）.设区间
当
时，曲线C上存在点
使得点Pn处的切线与直线AAn平行.
（Ⅰ）证明：
是等比数列；
|
对一切
恒成立时，求t的取值范围；
（Ⅲ）记数列{an}的前n项和为Sn，当
时，试比较Sn与n+7的大小，并证明你的结论.
陕西省西安市2007年高三年级八校联考
数学试题（理）参考答案
一、选择题（每小题5分，共60分）
1．D 2．B 3．C 4．A 5．B 6．A 7．D 8．C 9．A
10．D 11．B 12．C
二、填空题（每小题4分，共16分）
13．
14．
15．
16．
三、解答题（共74分）
17．（Ⅰ）
（2分）
∴由
即cos=sin. （4分）
又
∴
（6分）
（Ⅱ）由
，得cos（cos－3）+sin（sin－3）=－1
即sin+cos=
（8分）
两边平方，得2sincos=
. （9分）
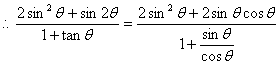
（12分）
18．（Ⅰ）∵
（3分）
∴
解得n=－1（舍去）或n=4.
即袋中有4个黑球. （5分）
（Ⅱ）可能的取值为0，1，2，3，4. （6分）
∵
（8分）
∴的概率分布列为
|
| 0 | 1 | 2 | 3 | 4 |
| P |
|
|
|
|
|
（10分）
（12分）
19．（Ⅰ）∵PD=CD=1，PC=
∴PD2+CD2=PC2，即PD⊥CD. （3分）
又PD⊥平面ABCD. （6分）
（Ⅱ）如图，连结AC交BD于O，则AC⊥BD.
∵PD⊥平面ABCD，
∴PD⊥AC.
∴AC⊥平面PBD. （8分）
过O点作OE⊥PB于E，连结AE，
则AE⊥PB，故∠AEO为二面角
|
角. （10分）
由Rt△OEB∽Rt△PDB，得
OE=
.
∴tan∠AEO=
即∠AEO=60° （22分）
20．（Ⅰ）
（1分）
令
得
的单调递增区间为（a,3a）
令
得的单调递减区间为（－
，a）和（3a，+） （4分）
∴当x=a时，极小值=
当x=3a时，极小值=b. （6分）
（Ⅱ）由
≤a，得－a≤－x2+4ax－3a2≤a.①（7分）
∵0<a<1，
∴a+1>2a.
∴
上是减函数. （9分）
∴
于是，对任意
，不等式①恒成立，等价于
又
∴
（12分）
21．（Ⅰ）依题意，设双曲线方程为
∴双曲线的两条渐近线为
=0 （2分）
又圆A的方程为
∴
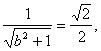得b=1.
故所求双曲线方程为
（6分）
（Ⅱ）显然，l与x轴不垂直，设l：y=kx+1.
由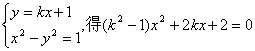
（8分）
显然，
设B（x1,y1）、C（x2,y2）（x1<0,x2<0）则
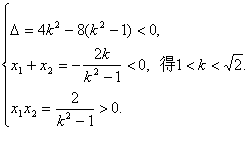（9分）
又由
（10分）
∴
故
=0 （12分）
22．（Ⅰ）∵由线在点Pn的切线与直线AAn平行，
∴
（1分）
由
（2分）
∴
即
∴是首项为
2+1为首项，公比为2的等比数列. （4分）
（Ⅱ）由（Ⅰ）得
=（2+1）·2n-1，
∴
从而an=2xn－1=1+
（6分）
|
Dn，得an+1<an，即（2t）2n<（2t）
. （8分）
∴0<2t<1，即0<t<
（9分）
（Ⅲ）当时，
（10分）
∴
不难证明：当n≤3时，2n-1≤n+1；当n≥4时，2n-1>n+1. （11分）
∴当n≤3时，
（12分）
当n≥4时，
（13分）
综上所述，对任意的
（14分）