高三年级最后一次冲刺试卷（数学）

淮安市车桥中学2007届高三年级最后一次冲刺试卷

数学试卷　 2007-5-26

注　意　事　项 考生在答题前请认真阅读本注意事项及各题答题要求 1、本试卷共4页，包含选择题（第1题～第10题，共10题）、填空题（第11题～第16题，共6题）、解答题（第17题～第21题，共5题）三部分。本次考试时间为120分钟。考试结束后，请将本试卷和答题卡一并交回。 2、答题前，请您务必将自己的姓名、考试证号用书写黑色字迹的0.5毫米签字笔填写在试卷及答题卡上。 3、请认真核对监考员所粘贴的条形码上的姓名、考试证号是否与您本人的相符。 4、作答非选择题必须用书写黑色字迹的0.5毫米签字笔写在答题卡上的指定位置，在其它位置作答一律无效。作答选择题必须用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动，请用橡皮擦干净后，再选涂其它答案。 5、如有作图需要，可用2B铅笔作答，并请加黑加粗，描写清楚。

．如果事件Ａ在一次试验中发生的概率是Ｐ，那么次独立重复试验中恰好发生次的概率是

参考公式

　　　 ．如果事件Ａ、Ｂ互斥，那么

　　　　　　　

　　　 ．如果事件Ａ、Ｂ相互独立，那么

　　　　　　　

一组数据的方差

　　　　　　　　其中为这组数据的平均数

一．选择题：在每小题列出的四个选项中，只有一项是符合题目要求的。本大题共10小题，每小题5分，共50分。

1. 抛物线的焦点坐标是 　　　　　　　　　　　　　　　　　　　　　　　　　( 　)

A、　　　　 B、　　　　C、　　　　  D、

2. 已知a,b都是实数,则“a＜b＜0”是“＞”的（　　）条件

A.充分非必要　　　B.必要非充分　　　 C. 充要　　　　　 D.非充分非必要

3. 函数的反函数是　　　　　　　　　　　　　　　　　　　　　　　 （　 ）

A．　　 　　 B．　

C．　　　　 D．

4.如图，△ABC是Rt△AB为斜边，三个顶点A、B、C在平面α内的射影分别是A₁、B₁、C₁.如果△A₁B₁C₁是等边三角形，且AA₁＝m，BB₁＝m＋2,CC₁＝m＋1,并设平面ABC与平面A₁B₁C₁所成的二面角的平面角为则的值为　　　　（　　  ）

　　（A）　　　　　（B）　　　　（C）　　　　 （D）

5．从集合{1，2，3，…，11}中任选2个元素作为椭圆方程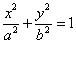中的a和b，则能落在矩形区域　　　 内的椭圆个数为　　　　　　 　　　　　　　　　　　　　（　 ）

　　A． 43　　　　　  B。 72　　　　　　　 C。 86　　　　　　  D。 90

6. 已知函数在上是增函数，，若，则的取值范围是 (　 )

A、　　　　 B、　　　　　 C、　　　 D、

7.设变量、满足约束条件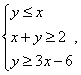则目标函数的最小值为 　　　　　　　　 (　 )

　　　 （A）2　　　　（B）3　　　　（C）4　　　　（D）9

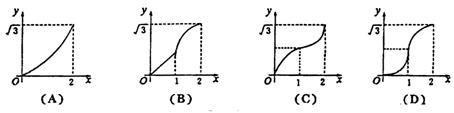
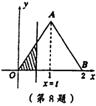8．如图所示，在直角坐标系的第一象限内，△AOB是边长为2的等边三角形，设直线x=t（0≤t≤2）截这个三角形可得位于此直线左方的图形（阴影部分）的面积为f（t），则函数y=f（t）的图象（如下图所示）大致是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　 ）　

9.给出以下四个命题

①如果一条直线和一个平面平行,经过这条直线的一个平面和这个平面相交,那么这条直线和交线平行;

②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面;

③如果两条直线都平行于一个平面,那么这两条直线互相平行;

④如果一个平面经过另一个平面的一条垂线,那么些两个平面互相垂直.

其中真命题的个数是　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）　　　

A.4　　　　　  B.3　　　　　  C.2　　　　　  D.1

10．某宇宙飞船的运行轨道是以地球的中心F为左焦点的椭圆，测得近地点A距离地面m

千米，远地点B距离地面n千米，地球的半径为k千米.关于椭圆有以下四种说法：

　　①焦距长为n－m；②短轴长为；③离心率为；

　　④以AB方向为x轴的正方向，F为坐标原点，则左准线方程为

　　以上正确的说法有　　　　　　　　　　　　　　　　　　　　　　　　 （　　）　

　　 A．①③　　　 B．②④　　　　　C．①③④　　　　D．①②④

二．填空题：本大题共6小题，每小题5分，共30分。把答案填在答题卡的相应位置

11.不等式的解集是　　　　　　

12. ,则方程可以表示不同直线的条数为　　　　　　

13.用数字0、1、2、3、4组成没有重复数字的五位数，则其中数字1、2相邻的偶数有＿＿＿＿个（用数字作答）

14. 接种某疫苗后，出现发热反应的概率为0.80.现有5人接种该疫苗，至少有3人出现发热反应的概率为___________.（精确到0.01）

.15．定义：若存在常数，使得对定义域内的任意两个，均有 成立，则称函数在定义域上满足利普希茨条件。若函数满足利普希茨条件，则的最小值为 　　　　　　　　　  。　　　

16 若函数的图象与直线有且仅有四个不同的交点，则的取值范围是______　　　 

三．解答题：本大题共5小题，共70分。解答应写出文字说明，证明过程或演算步骤。

17.(本小题满分12分)

已知向量

　　(Ⅰ)求sinα-cosα的值； (Ⅱ)求的值.

18（本小题满分14分）．

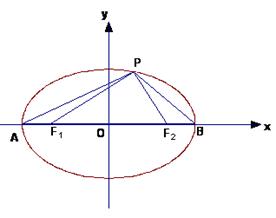
设椭圆的两焦点坐标分别为F₁（和F₂，它与轴的两交点分别为A、B，点P为椭圆上一点，若F₁P⊥PF₂，，求椭圆方程.

19（本小题满分14分）

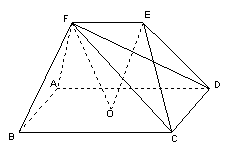　如图，在五面体ABCDEF中，点O是矩形ABCD的对角线的交点，面CDE是等边三角形，棱

　　　 （I）证明平面

　　　 （II）设证明平面

20.(本小题满分14分)

　学校餐厅每天供应1000名学生用餐，每星期一有A、B两样菜可供选择，调查资料表明，凡是在本周星期一选A菜的，下周星期一会有20%改选B菜，而选B菜的，下周星期一则有30%改选A菜，若A_n、B_n分别表示在第n个星期一选A、B菜的人数.

　(1)试以A_n表示A_n+1；

(2)若A₁=200，求{A_n}的通项分式；

(3)问第几个星期一时，选A菜与选B菜的人数相等？

21．（本小题满分16分）

在直角坐标平面中，ΔABC的两个顶点AB的坐标分别为A(―a，0)，B(a，0)(a>0)，

两动点M，N满足++=0，==，向量与共线.

(1)求ΔABC的顶点C的轨迹方程；

(2)若过点P(0，a)的直线与(1) 轨迹相交于E、F两点，求·的取值范围；

(3)(理科作)若G(―a，0)，H(2a，0)，Q点为C点轨迹在第一象限内的任意一点，则是否存在常数λ(λ>0)，使得∠QHG=λ∠QGH 恒成立？若存在，求出的值；若不存在，请说明理由.

参考答案：

一、选择题：1—5 DA B CB,　 6---10 AD D BC

二、填空题：(11).(-∞,0)∪(2,+ ∞) ; (12). 13; (13).24; (14). 0.94; (15). ; (16). 1≤k＜

17．解；(Ⅰ)∵=(sinα,1)共线　　 ∴sinα+cosα=　… 2分

　 故sin2α=- txj从而(sinα-cosα)²=1-sin2α=　… 4分t

∵α∈(-)∴sinα<0，cosα>0　　∴sinα-cosα= - … 6分

(Ⅱ)∵=2cos²α=1+cos2α… 9分

又cos2α=cos²α-sin²α=(cosα+sinα)(cosα-sinα)= ∴原式=1+…12分

18解：由于∠F₁PF₂=90⁰，则，

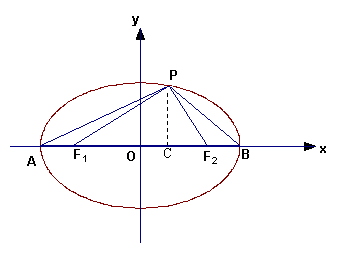∴，设点P在第一象限，则

∴，由于，，

∴

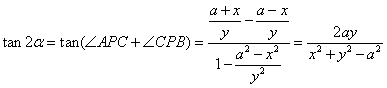
而，∴

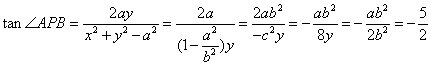
∴ ，故所求的椭圆方程为.

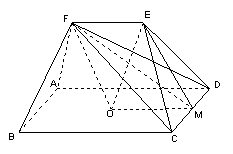19）本小题考查直线与平面平行、直线与平面垂直等基础知识，考查空间想象能力和推理论证能力。满分14分。

　　　 （I）证明：取CD中点M，连结OM。

　　　 在矩形ABCD中，

　　　 又

　　　 则连结EM，于是

　　　 四边形EFOM为平行四边形。

　　　

　　　 又平面CDE，且平面CDE，平面CDE。…6 分

　　　 （II）证明：连结FM。由（I）和已知条件，在等边中，

　　　 且

　　　 因此平行四边形EFOM为菱形，从而。

　　　 平面EOM，从而

　　　 而所以平面 … 14分

20.解：(1)依题意，得　①

　　将B_n=1000-A_n代入①，

　　得A_n+1=0.5A_n+300.　②　　　　　　　　　　　　　　　　　　　　　　　　　 4分

　　

(2)设A_n+1+λ=0.5(A_n+λ)，即A_n+1=0.5A_n-0.5λ，得-0.5λ=300，∴λ=-600.

　　∴{A_n-600}是以A₁-600=200-600=-400为首项，公比为0.5的等比数列.

　　∴A_n-600=-400×0.5^n-1.

　　∴A_n=600-400×0.5^n-1.　　　　　　　　　　　　　　　　　　　　　　　　　 10分

　　

(3)∵A_n=B_n，且A_n+B_n=1000，∴A_n=500，得600-400×0.5^n-1=500.∴0.5^n-1=0.5²，n-1=2.

　　∴n=3，即第三个星期一时，选A菜与选B菜的人数相等.　　　　　　　　　  14分

21． (1)设(x，y)，∵++=0，∴M点是ΔABC的重心，∴M(，).

又=且向量与共线，∴N在边AB的中垂线上，∴N(0，).

而=，∴=，即x²― =a².

(2)设E(x₁，y₁)，F(x₂，y₂)，过点P(0，a)的直线方程为y=kx+a，

代入x²― =a²得 (3―k²)x²―2akx―4a²=0

∴Δ=4a²k²+16a²(3―k²)>0，即k²<4. ∴k²―3<1，∴>4或<0.

而x₁，x₂是方程的两根，∴x₁+x₂=，x₁x₂=.

∴·=(x₁，y₁―a)·(x₂，y₂―a)= x₁x₂+kx₁·kx₂=(1+k²) x₁x₂==4a²(1+)∈(－∞， 4a²)∪(20a²，＋∞).

故·的取值范围为(－∞，4a²)∪(20a²，＋∞).

(3) 设Q(x₀，y₀) (x₀>0，x₀>0)，则x₀²― =a²，即y₀²=3(x₀²―a₀²).

当QH⊥x轴时，x₀=2a，y₀=3a，∴∠QGH=，即∠QHG= 2∠QGH，故猜想λ=2，

使∠QHG=λ∠QGH总成立.

当QH不垂直x轴时，tan∠QHG=―，tan∠QGH= ，

∴tan2∠QGH= = = = =―= tan∠QHG.

又2∠QGH与∠QHG同在(0，)∪(，π)内，∴2∠QGH=∠QHG.

故存在λ=2，使2∠QGH=∠QHG恒成立.