江西省重点中学联考盟校2007届高三年级第二次模拟考试
数学(文)试题
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.设集合![]() = ( )
= ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
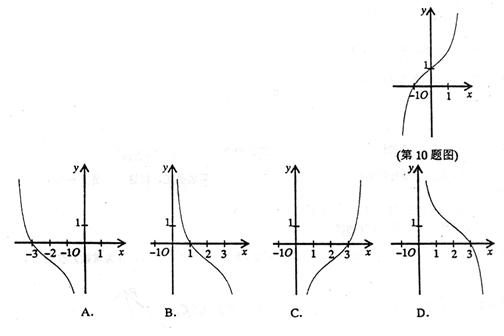
2.函数![]() 的反函数是 ( )
的反函数是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.在![]() 的展开式中,
的展开式中,![]() 的系数是 ( )
的系数是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知向量![]() ,则
,则![]() 可表示为 ( )
可表示为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.在△ABC中,A=45°,AB=![]() ,则“BC=
,则“BC=![]() ”是“△ABC只有一解且C=60°”的
”是“△ABC只有一解且C=60°”的
( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既为充分也不必要条件
6.已知函数![]() ,则 ( )
,则 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]() 的大小不能确定
的大小不能确定
7.一年级有12个班,每个班的同学从1到50排学号,为了交流学习经验,要求每班学号
为14的同学留下来进行交流,这里运用的是 ( )
A.分层抽样 B.抽签抽样 C.随机抽样 D.系统抽样
8.过抛物线焦点F的直线与抛物线相交于A、B两点,若A、B在抛物线准线上的射影分别
是A1、B1,则∠A1FB1等于 ( )
A.75° B.90° C.105° D.120°
9.设![]() 是函数
是函数![]() 定义域内的两个变量,且
定义域内的两个变量,且![]() ,若
,若![]() ,那
,那
么下列不等式恒成立的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
|
|
11.已知正三棱锥P—ABC的体积为![]() 外接球球心为O,且满足
外接球球心为O,且满足![]() ,则正三棱锥P—ABC的外接球半径为 ( )
,则正三棱锥P—ABC的外接球半径为 ( )
A.1 B.![]() C.
C.![]() D.2
D.2
12.从数字1,2,3,…,10中,按由小到大的顺序取出![]() 则不同的取法有( )种 ( )
则不同的取法有( )种 ( )
A.52 B.54 C.56 D.58
二、填空题(本大题共4小题,每小题4分,共16分,把答案填在题中横线上。)
13.若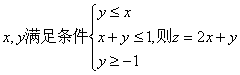 的最大值是
。
的最大值是
。
14.等差数列有如下性质,若数列![]() 是等差数列,则当
是等差数列,则当![]() 也是等差数列;类比上述性质,相应地
也是等差数列;类比上述性质,相应地![]() 是正项等比数列,当数列
是正项等比数列,当数列![]() 时,数列
时,数列![]() 也是等比数列。
也是等比数列。
15.不等式![]() ,则实数a=
。
,则实数a=
。
|
三、解答题(本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤)。
17.(本大题满分12分)已知函数![]()
(1)求![]() 的最小正周期;
的最小正周期;
(2)若![]() ,求
,求![]() 的最大值、最小值及相应的x的值。
的最大值、最小值及相应的x的值。
18.(本大题满分12分)某工厂举行羽毛球选拔赛,由三个车间各推荐两名员工,将这六名员工平均分成3组进行比赛。
(1)求有且只有一个组的两名员工来自同一车间的概率
(2)求每组的两名员工均不来自同一车间的概率
19.(本大题满分12分)求函数![]() 取极小值时x的值。
取极小值时x的值。
|
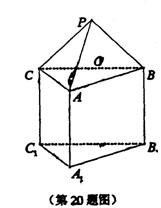
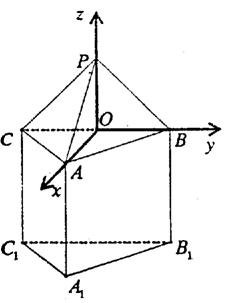
△PBC是全等的正三角形。BC中点为O。
(1)求证:BC1⊥平面AOB1;
(2)求平面PAB与平面BB1C所成的
锐二面角的大小;
(3)点B在平面AB1O内的射影为G,
求点G到平面PAB的距离。
21.(本大题满分12分)已知数列![]() 为等比数列,
为等比数列,![]() 对于满足
对于满足![]() 的整数k,数列
的整数k,数列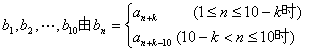 确定记
确定记
![]() 。
。
(1)求数列![]() 的通项公式;
的通项公式;
(2)当![]() 时,求
时,求![]() 的值。
的值。
|
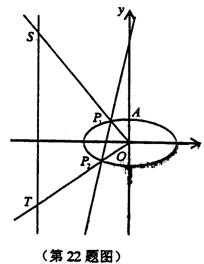
(1)求椭圆C的方程
(2)若直线l的似斜角![]()
与椭圆的左准线分别交于点S、T,求[ST]的取
值范围。
参考答案
一、选择:
1.C 2.C 3.D 4.A 5.B 6.B 7.D 8.B 9.B 10.C 11.B 12.C
|
13.3 14.![]() 15.
15.![]() 16.②③④⑤
16.②③④⑤
三、填空题
17.解:(1)![]()
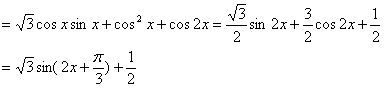
![]() …………6分
…………6分
(2)由![]()
![]()
![]() …………12分
…………12分
18.解:(1)![]()
![]() …………6分
…………6分
(2)![]() ,三个组的员工都来自同一车间的情况有1种
,三个组的员工都来自同一车间的情况有1种
∴![]() ………………(12分)
………………(12分)
19.解:![]()
(1)当![]() 取得极小值
取得极小值
(2)当![]() 无极值点
无极值点
(3)当![]() 取得极小值
取得极小值
(4)当![]() 取得极大值,无极小值
取得极大值,无极小值
(5)当![]() 取得极小值
取得极小值
|
20.解:(1)由题意PA=AB=PA=AC=PC=1
∴AO⊥BC![]() AO⊥平面BB1C1C
AO⊥平面BB1C1C![]() AO⊥BC1
AO⊥BC1
又![]() 在矩形BB1C1C中B1O⊥BC1
在矩形BB1C1C中B1O⊥BC1
∴BC1⊥平面AOB1 …………4分
(2)由题意得
PA=AB=PA=AC=PC=1且BC=![]()
∴PO=AO=![]()
∴PO⊥CB PO⊥AO![]() PO⊥平面ABC
PO⊥平面ABC
∴PO//BB1 ∴P点在平面BB1C内
∴所求锐二面角即二面角A—PB—O,其中A在平面PBO上的射影即点O
由AO=![]() ,而A点到PB的距离为
,而A点到PB的距离为![]() ,
,
∴所求锐二面角为![]() …………8分
…………8分
(3)∵BC1⊥平面AOB1
∴B在平面AB1O内的射影为G即BC1与OB1的交点
设所求距离为h,由S△BGP=![]() S
S![]() ,
,
![]()
![]() …………12分
…………12分
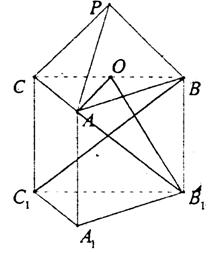
解法二:由题意,如图建立空间直角坐标系
|
![]()
![]()
(1)![]()
![]()
![]()
![]() ………………(4分)
………………(4分)
(2)平面PAB有法向量![]() 平面BB1C的法向量
平面BB1C的法向量![]()
![]()
∴所求锐二面角为arcos![]() ………………(8分)
………………(8分)
(3)![]()
∴![]()
平面PAB有法向量![]() 由
由![]()
∴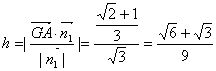 ………………(12分)
………………(12分)
21.解:(1)由![]() …………(4分)
…………(4分)
(2)由![]() 时,
时,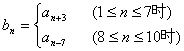 …………(8分)
…………(8分)
![]()
![]()
![]() ………………12分
………………12分
22.解:(1)设![]() ,得
,得
![]()
![]() ………………4分
………………4分
(2)设直线l的方程为![]()
∵倾斜角![]()
∴![]()
则P1(x1,y1),P2(x2,y2)的坐标轴满足方程组
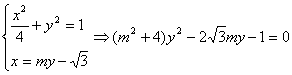 …………(6分)
…………(6分)
![]()
![]()
由P1(x1,y1),P2(x2,y2),得直线OP1、OP2的方程为
![]() ………………(8分)
………………(8分)
∴点S、T的坐标为![]()
∴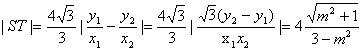 ………………(10分)
………………(10分)
令![]()
∴![]() ………………(14分)
………………(14分)