江西省重点中学联考盟校2007届高三年级第二次模拟考试
数学(理)试题
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.复数![]() 是纯虚数,则实数a的值为 ( )
是纯虚数,则实数a的值为 ( )
A.1 B.2 C.-2 D.2或1
2.函数![]() 的反函数是 ( )
的反函数是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.在![]() 的展开式中,
的展开式中,![]() 的系数是 ( )
的系数是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知向量![]() ,若正数k和t使得向量
,若正数k和t使得向量![]() 互相垂直,则k的最小值为 ( )
互相垂直,则k的最小值为 ( )
A.1 B.2 C.4 D.8
5.在△ABC中,A=45°,AB=![]() ,则“BC=
,则“BC=![]() ”是“△ABC只有一解且C=60°”的
”是“△ABC只有一解且C=60°”的
( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既为充分也不必要条件
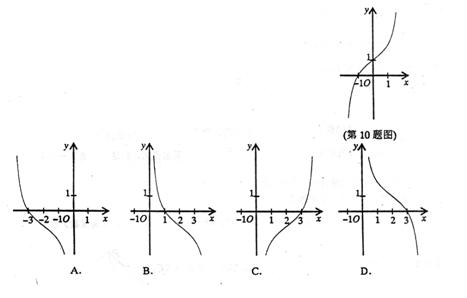
6.已知函数![]() ,则 ( )
,则 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]() 的大小不能确定
的大小不能确定
7.下列命题中,真命题是 ( )
A.![]() B.
B.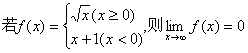
C.![]() D.
D. ![]()
8.若以圆锥曲线的一条经过焦点的弦为直径的圆与对应的准线无公共点,则此圆锥曲线为
( )
A.椭圆 B.双曲线 C.抛物线 D.椭圆或双曲线
9.设![]() 是函数
是函数![]() 定义域内的两个变量,且
定义域内的两个变量,且![]() ,若
,若![]() ,那
,那
么下列不等式恒成立的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
|
|
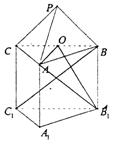
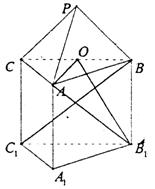
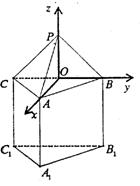
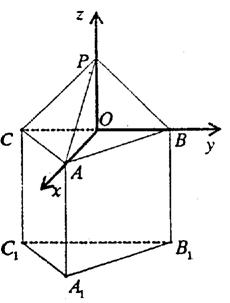
11.已知正三棱锥P—ABC的体积为![]() 外接球球心为O,且满足
外接球球心为O,且满足![]() ,则正三棱锥P—ABC的外接球半径为 ( )
,则正三棱锥P—ABC的外接球半径为 ( )
A.1 B.![]() C.
C.![]() D.2
D.2
12.从数字1,2,3,…,10中,按由小到大的顺序取出![]() 则不同的取法有( )种
则不同的取法有( )种
A.52 B.54 C.56 D.58
二、填空题(本大题共4小题,每小题4分,共16分,把答案填在题中横线上。)
13.若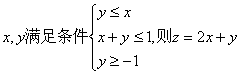 的最大值是
。
的最大值是
。
14.等差数列有如下性质,若数列![]() 是等差数列,则当
是等差数列,则当![]() 也是等差数列;类比上述性质,相应地
也是等差数列;类比上述性质,相应地![]() 是正项等比数列,当数列
是正项等比数列,当数列![]() 时,数列
时,数列![]() 也是等比数列。
也是等比数列。
15.已知随机变量![]() =
.
=
.
(参考数据:Φ(0.25)=0.5987,Φ(0.5)=0.6915,Φ(1)=0.8413,Φ(1.5)=0.9332)
|
三、解答题(本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤)。
17.(本大题满分12分)已知函数![]()
(1)求![]() 的最小正周期;
的最小正周期;
(2)若![]() ,求
,求![]() 的最大值、最小值及相应的x的值。
的最大值、最小值及相应的x的值。
18.(本大题满分12分)某工厂举行羽毛球选拔赛,由三个车间各推荐两名员工,将这六名员工平均分成3组进行比赛。
(1)求有且只有一个组的两名员工来自同一车间的概率
(2)设有![]() 个组的两名员工来自同一车间,求
个组的两名员工来自同一车间,求![]() 的分布列和期望.
的分布列和期望.
|
(1)求证:BC1⊥平面AOB1;
(2)求平面PAB与平面BB1C所成的锐二面角的大小;
(3)点B在平面AB1O内的射影为G,求点G到平面PAB的距离。
20.(本大题满分12分)
若函数![]()
(1)求函数![]() 的单调区间
的单调区间
(2)若对所有的![]() 成立,求实数a的取值范围.
成立,求实数a的取值范围.
21.(本大题满分12分)
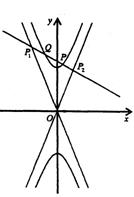
如图,已知双曲线![]() 的离心率
的离心率![]() 、F2分别为双曲线C的上、下焦点,M为上准线与渐近线在第一象限的交点,且
、F2分别为双曲线C的上、下焦点,M为上准线与渐近线在第一象限的交点,且![]() =-1
=-1
|
(2)直线l交双曲线C的渐近线l1、l2于P1、P2,
交双曲线上支于P、Q,且![]() 的最小值.
的最小值.
22.(本大题满分14分)
在![]() 个不同数的排列
个不同数的排列![]() (即前面某数大于后面某数)则称
(即前面某数大于后面某数)则称![]() 构成一个逆序,一个排列的全部逆序的总数称为该排列的逆序数,例如排列(2,40,3,1)中有逆序“2与1”,“40与3”,“40与1”,“3与1”其逆序数等于4. 已知n+2
构成一个逆序,一个排列的全部逆序的总数称为该排列的逆序数,例如排列(2,40,3,1)中有逆序“2与1”,“40与3”,“40与1”,“3与1”其逆序数等于4. 已知n+2![]() 个不同数的排列
个不同数的排列![]() 的逆序数是2.
的逆序数是2.
(1)求(1,3,40,2)的逆序数;
(2)写出![]() 的逆序数an
的逆序数an
(3)令![]() .
.
参考答案
一、选择:
1.C 2.C 3.D 4.B 5.B 6.B 7.D 8.A 9.B 10.C 11.B 12.C
|
13.3 14.![]() 15.0.5328 16.②③④⑤
15.0.5328 16.②③④⑤
三、填空题
17.解:(1)![]()
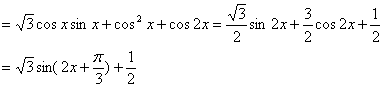
![]() …………6分
…………6分
(2)由![]()
![]()
![]() …………12分
…………12分
18.解:(1)![]()
![]() …………6分
…………6分
(2)![]() ,三个组的员工都来自同一车间的情况有1种
,三个组的员工都来自同一车间的情况有1种
![]()
|
| 0 | 1 | 3 |
| P |
|
|
|
![]() …………12分
…………12分
19.解:(1)由题意PA=AB=PA=AC=PC=1
|
又![]() 在矩形BB1C1C中B1O⊥BC1
在矩形BB1C1C中B1O⊥BC1
∴BC1⊥平面AOB1 …………4分
(2)由题意得
PA=AB=PA=AC=PC=1且BC=![]()
∴PO=AO=![]()
∴PO⊥CB PO⊥AO![]() PO⊥平面ABC
PO⊥平面ABC
∴PO//BB1 ∴P点在平面BB1C内
∴所求锐二面角即二面角A—PB—O,其中A在平面PBO上的射影即点O
由AO=![]() ,而A点到PB的距离为
,而A点到PB的距离为![]() ,
,
∴所求锐二面角为![]() …………8分
…………8分
(3)∵BC1⊥平面AOB1
∴B在平面AB1O内的射影为G即BC1与OB1的交点
设所求距离为h,由S△BGP=![]() S
S![]() ,
,
![]()
|
解法二:由题意,如图建立空间直角坐标系
由![]()
![]()
![]()
(1)![]()
![]()
![]() ………………(4分)
………………(4分)
(2)平面PAB有法向量![]() 平面BB1C的法向量
平面BB1C的法向量![]()
![]()
∴所求锐二面角为arcos![]() ………………(8分)
………………(8分)
(3)![]()
∴![]()
平面PAB有法向量![]() 由
由![]()
∴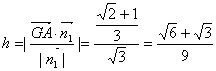 ………………(12分)
………………(12分)
19.解:(1)由题意PA=AB=PA=AC=PC=1
∴AO⊥BC![]() AO⊥平面BB1C1C
AO⊥平面BB1C1C![]() AO⊥BC1
AO⊥BC1
又![]() 在矩形BB1C1C中B1O⊥BC1
在矩形BB1C1C中B1O⊥BC1
∴BC1⊥平面AOB1 …………4分
(2)由题意得
PA=AB=PA=AC=PC=1且BC=![]()
∴PO=AO=![]()
∴PO⊥CB PO⊥AO![]() PO⊥平面ABC
PO⊥平面ABC
∴PO//BB1 ∴P点在平面BB1C内
∴所求锐二面角即二面角A—PB—O,其中A在平面PBO上的射影即点O
由AO=![]() ,而A点到PB的距离为
,而A点到PB的距离为![]() ,
,
∴所求锐二面角为![]() …………8分
…………8分
(3)∵BC1⊥平面AOB1
∴B在平面AB1O内的射影为G即BC1与OB1的交点
设所求距离为h,由S△BGP=![]() S
S![]() ,
,
![]()
![]() …………12分
…………12分
解法二:由题意,如图建立空间直角坐标系
|
![]()
![]()
(1)![]()
![]()
![]()
![]() ………………(4分)
………………(4分)
(2)平面PAB有法向量![]() 平面BB1C的法向量
平面BB1C的法向量![]()
![]()
∴所求锐二面角为arcos![]() ………………(8分)
………………(8分)
(3)![]()
∴![]()
平面PAB有法向量![]() 由
由![]()
∴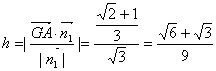 ………………(12分)
………………(12分)
20.解:(1)![]() 的定义域为
的定义域为![]() …………12分
…………12分
![]() …………2分
…………2分
![]()
①当![]() …………3分
…………3分
②![]() 时
时
![]()
![]() …………4分
…………4分
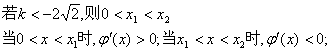
![]() …………5分
…………5分
综上:
![]()
单调递减区间为![]()
![]() 的单调递增区间(0,+
的单调递增区间(0,+![]() ) …………6分
) …………6分
(2)![]() …………7分
…………7分
![]() …………8分
…………8分
则![]() …………9分
…………9分
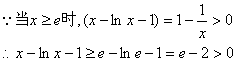
![]() …………10分
…………10分
![]() …………11分
…………11分
![]() …………12分
…………12分
另解:![]()
![]() …………7分
…………7分
![]() …………8分
…………8分
![]()
![]() 单增 …………9分
单增 …………9分
①当![]()
![]()
![]() …………11分
…………11分
②当![]()
![]()
![]() 不成立 …………12分
不成立 …………12分
综上所述![]()
21.解:(1)设![]()
![]()
![]() 故双方曲线方程为
故双方曲线方程为![]() …………6分
…………6分
(2)由题意,设直线l的方程为![]() 联立得
联立得
![]()
当![]() 、
、![]() 、P2的横坐标,
、P2的横坐标,
当![]() 、
、![]() 、Q的横坐标。
、Q的横坐标。
![]() …………9分
…………9分
![]()
![]() 、
、![]()
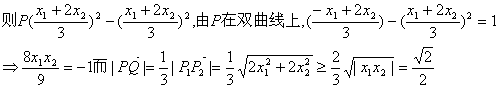
当且仅当![]() 时取等号 …………12分
时取等号 …………12分
另解:假设直线l的方程为![]() ,
,
交两渐近线于![]()
![]()
![]() ,由P点在双曲线上
,由P点在双曲线上
![]() …………9分
…………9分
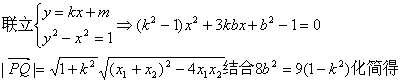
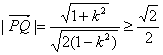 ,当且仅当k=0时取等号 …………12分
,当且仅当k=0时取等号 …………12分
22.解:(1)![]() …………4分
…………4分
(2)n+2个数中任取两个数比较大小,共有![]() 个大小关系
个大小关系
![]() …………8分
…………8分
(3)![]()
![]()
![]()
![]() …………14分
…………14分