市北中学08届高三第一学期期中数学(理科)测试卷
(考试时间:120分钟 满分:150分)
姓名___________班级_________学号_________得分__________
| 题 号 | 一 | 二 | 三 | 总 分 | |||||
| 1—11 | 12—15 | 16 | 17 | 18 | 19 | 20 | 21 | ||
| 得 分 | |||||||||
|
一.填空题 (本大题满分44分)本大题共有11题,只要求直接
填写结果,每题填对得4分,否则一律得零分.
1.已知集合![]() ,
,![]() ,则
,则![]() _____________.
_____________.
2.设![]() 则
则![]() 的值等于______________.
的值等于______________.
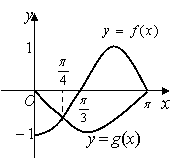 3.同时具有性质:①最小正周期为2p;②图象关于直线
3.同时具有性质:①最小正周期为2p;②图象关于直线![]() 对称的一个函数是___________.
对称的一个函数是___________.
4.已知函数![]() 是偶函数,
是偶函数,![]() 是奇函数,它们的
是奇函数,它们的
定义域是![]() ,且它们在
,且它们在![]() 上的图象如图所示,
上的图象如图所示,
则不等式![]() 的解集是
.
的解集是
.
5.在△ABC中,BC=1,![]() ,当△ABC的面积等于
,当△ABC的面积等于![]() 时,
时,![]() .
.
6.f(x)是定义域为R,最小正周期为![]() 的函数,若
的函数,若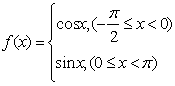 ,则
,则![]() 的值等于___________
的值等于___________
7.函数![]()
![]() 的图象恒过定点
的图象恒过定点![]() ,若点
,若点![]() 在一次函数
在一次函数![]() 的图象上,其中
的图象上,其中![]() ,则
,则![]() 的最小值为
.
的最小值为
.
8.已知二次函数![]() ,若在区间[0,1]内至少存在一个实数
,若在区间[0,1]内至少存在一个实数![]() ,使
,使![]() ,则实数
,则实数![]() 的取值范围是_____________.
的取值范围是_____________.
9.定义在![]() 上的函数
上的函数![]() ,给出下列性质:①
,给出下列性质:①![]() 是增函数;
是增函数;
②![]() 是减函数;③
是减函数;③![]() 有最大值; ④
有最大值; ④![]() 有最小值。其中正确的命题是__________.
有最小值。其中正确的命题是__________.
10.已知函数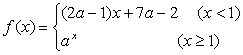 在(-∞,+∞)上单调递减,则实数a的取值范围是________________.
在(-∞,+∞)上单调递减,则实数a的取值范围是________________.
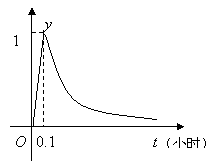 11.为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气中的含药量
11.为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气中的含药量![]() (毫克)与时间
(毫克)与时间![]() (小时)成正比;药物释放完毕后,
(小时)成正比;药物释放完毕后,![]() 与
与![]() 的函数关系式为
的函数关系式为![]() (
(![]() 为常数),如右图所示。根据图中提供的信息,回答下列问题:若当空气中每立方米的含药量降低到
为常数),如右图所示。根据图中提供的信息,回答下列问题:若当空气中每立方米的含药量降低到![]() 毫克以下时,学生方可进教室,那么从药物释放开始,至少需要经过 小时后,学生才能回到教室.
毫克以下时,学生方可进教室,那么从药物释放开始,至少需要经过 小时后,学生才能回到教室.
|
二.选择题(本大题满分16分)本大题共有4题,每题都给出代号为A、B、C、D的四个结论,其中有且只有一个结论是正确的,必须把正确结论的代号写在题后的圆括号内,选对得4分,不选、选错一律得零分.
12. ![]() ,
,![]() 是定义在
是定义在![]() 上的函数,
上的函数,![]() ,则“
,则“![]() ,
,![]() 均为偶函数”是“
均为偶函数”是“![]() 为偶函数”的……………………………………………………..( )
为偶函数”的……………………………………………………..( )
A.充要条件 B. 必要而不充分的条件
C.充分而不必要的条件 D.既不充分也不必要的条件
13.在三角形ABC中,若![]() 则此三角形必是………………( )
则此三角形必是………………( )
A.等腰三角形 B.正三角形 C.直角三角形 D.等腰直角三角形
14.函数![]() 的反函数是…………………………………………( )
的反函数是…………………………………………( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
15.给出下列三个等式:![]() ,
,![]() ,
, ![]() ,下列函数中,对于定义域中任意
,下列函数中,对于定义域中任意![]() ,不满足其中任何一个等式的是……………( )
,不满足其中任何一个等式的是……………( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
|
16. (本题满分12分)
![]()
|
17. (本题满分12分)
已知函数![]()
(1)求函数![]() 的表达式; (2)若
的表达式; (2)若![]() ,求
,求![]() 的取值范围.
的取值范围.
|
在![]() 中,已知内角
中,已知内角![]() ,边
,边![]() .设内角
.设内角![]() ,
,
周长为![]() .
.
(1)求函数![]() 的解析式和定义域;
的解析式和定义域;
(2)求![]() 的最大值.
的最大值.
|
运货卡车以每小时![]() 千米的速度匀速行驶130千米, 按交
千米的速度匀速行驶130千米, 按交
通法规限制![]() (单位: 千米/小时).
假设汽油的价格是每升2元, 而汽车每小时耗油
(单位: 千米/小时).
假设汽油的价格是每升2元, 而汽车每小时耗油![]() 升, 司机的工资是每小时14元.
升, 司机的工资是每小时14元.
(1) 求这次行车总费用![]() 关于
关于![]() 的表达式;
的表达式;
(2) 当![]() 为何值时, 这次行车的总费用最低, 并求出最低费用的值.
为何值时, 这次行车的总费用最低, 并求出最低费用的值.
(精确到小数点后两位)
|
20. (本题满分18分)
设函数![]() ,其中m为常数且
,其中m为常数且![]() .
.
(1)解关于![]() 的不等式
的不等式![]() ;
;
(2)试探求![]() 存在最小值的充要条件,并求出相应的最小值.
存在最小值的充要条件,并求出相应的最小值.
|
21. (本题满分20分)
给出定义:若![]() (其中
(其中![]() 为整数),则
为整数),则![]() 叫做离实数
叫做离实数![]() 最近的整数,记作
最近的整数,记作![]() ,即
,即 ![]() . 在此基础上有函数
. 在此基础上有函数![]() .
.
(1)求![]() 的值;
的值;
(2)对于函数![]() ,现给出如下一些判断:
,现给出如下一些判断:
①
函数![]() 是偶函数;
是偶函数;
②
函数![]() 是周期函数;
是周期函数;
③
函数![]() 在区间
在区间![]() 上单调递增;
上单调递增;
④
函数![]() 的图像关于直线
的图像关于直线![]() 对称;
对称;
请你将以上四个判断中正确的结论全部选择出来,并选择其中一个加以证明;
(3)若![]() ,试求方程
,试求方程![]() 的所有解的和.
的所有解的和.
市北中学08届高三第一学期期中测试卷(理科)
参考答案与评分标准
1.![]() ; 2.
; 2.![]() ; 3.y=sin(x+
; 3.y=sin(x+![]() )等; 4.
)等; 4.![]() ; 5.
; 5.![]() ;
;
6.![]() ; 7.8; 8.(1,+∞); 9.① ③; 10.
; 7.8; 8.(1,+∞); 9.① ③; 10.![]() ; 11.0.6
; 11.0.6
12.C; 13.A; 14.D; 15.B
16.![]()

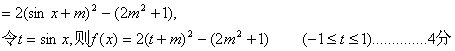
①![]()
![]() 7分
7分
②![]()
![]()
综上,![]() 12分
12分
17.已知函数![]()
(Ⅰ)求函数![]() 的表达式;
的表达式;
(Ⅱ)若![]() ,求
,求![]() 的取值范围.
的取值范围.
解:(Ⅰ)![]()
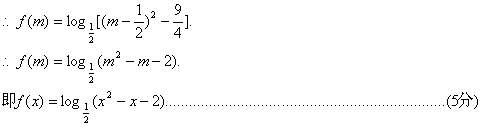
(Ⅱ)![]()
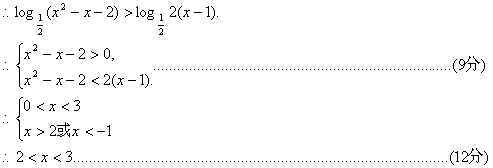
18.在![]() 中,已知内角
中,已知内角![]() ,边
,边![]() .设内角
.设内角![]() ,周长为
,周长为![]() .
.
(1)求函数![]() 的解析式和定义域;
的解析式和定义域;
(2)求![]() 的最大值.
的最大值.
解:(1)![]() 的内角和
的内角和![]() ,由
,由![]() 得
得![]() .…(2分)
.…(2分)
应用正弦定理,知
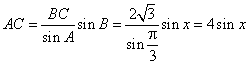 ,………………………………………..(2分)
,………………………………………..(2分)
![]() .………………………………………………(2分)
.………………………………………………(2分)
因为![]() ,
,
所以![]() ,…………………………(2分)
,…………………………(2分)
(2)因为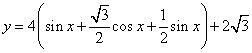 …………………………(2分)
…………………………(2分)
![]() ,………………………(2分)
,………………………(2分)
所以,当![]() ,即
,即![]() 时,
时,![]() 取得最大值
取得最大值![]() .…………………………(2分)
.…………………………(2分)
19.运货卡车以每小时x千米的速度匀速行驶130千米, 按交通法规限制![]() (单位: 千米/小时).
假设汽油的价格是每升2元, 而汽车每小时耗油
(单位: 千米/小时).
假设汽油的价格是每升2元, 而汽车每小时耗油![]() 升, 司机的工资是每小时14元.
升, 司机的工资是每小时14元.
(1) 求这次行车总费用y关于x的表达式;
(2) 当x为何值时, 这次行车的总费用最低, 并求出最低费用的值.
(精确到小数点后两位)
解: (1) 设行车所用时间为![]() ………………………………………(1分)
………………………………………(1分)
![]() ……………………………(6分)
……………………………(6分)
所以, 这次行车总费用y关于x的表达式是
![]()
(或:![]()
![]() ……………………………………(8分)
……………………………………(8分)
(2)![]() ,
,![]() ………………(11分)
………………(11分)
仅当![]() 时,
时,
上述不等式中等号成立…………………………………………………(13分)
答:当x约为56.88km/h时, 行车的总费用最低, 最低费用的值约为82.16元.……………………………………………………………………………(14分)
20.设函数f(x)=x-m-mx,其中m为常数且m<0。
(1)解关于x的不等式f(x)<0;
(2)试探求f(x)存在最小值的充要条件,并求出相应的最小值.
解:(1)由f(x)<0得,x-m<mx,得-mx<x-m<mx,即![]() ……2分
……2分
①当m=-1时,![]() x<-…………………………………………………4分
x<-…………………………………………………4分
②当-1< m<0时,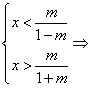 <x<……………………………………6分
<x<……………………………………6分
③当m<-1时,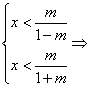 x<………………………………………………8分
x<………………………………………………8分
综上所述,当m<-1时,不等式解集为{xx<}
当m=-1时,不等式解集为{xx<-}
当-1<m<0时,不等式解集为{x<x<}………………………10分
(2)f(x)= ![]()
∵m<0,∴1-m>0,f(x)在[m,+∞)上单调递增,要使函数f(x)存在最小值,则f(x)在(-∞,m)上是减函数或常数,∴-(1+m)≤0即m≥-1,又m<0,∴-1≤m<0。
故f(x)存在最小值的充要条件是-1≤m<0,且f(x)min= f(m)=-m2. …………………18分
21. 给出定义:若![]() (其中
(其中![]() 为整数),则
为整数),则![]() 叫做离实数
叫做离实数![]() 最近的整数,记作
最近的整数,记作![]() ,即
,即 ![]() . 在此基础上有函数
. 在此基础上有函数![]() .
.
(1)求![]() 的值;
的值;
(2)对于函数![]() ,现给出如下一些判断:
,现给出如下一些判断:
①
函数![]() 是偶函数;
是偶函数;
②
函数![]() 是周期函数;
是周期函数;
③
函数![]() 在区间
在区间![]() 上单调递增;
上单调递增;
④
函数![]() 的图像关于直线
的图像关于直线![]() 对称;
对称;
请你将以上四个判断中正确的结论全部选择出来,并选择其中一个加以证明;
(3)若![]() ,试求方程
,试求方程![]() 的所有解的和.
的所有解的和.
21.解:
(1)![]() =0,
=0,![]() =
=![]() ,
, ![]() =0.3. ………………………6分
=0.3. ………………………6分
(2)正确结论有:①②④. ………………………………………………………………9分
证①:当![]() ,
,![]() 时,
时,![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]()
![]() ;
;
当![]() ,
,![]() 时,
时,![]() ,故函数
,故函数![]() 是偶函数. …14分
是偶函数. …14分
证②:对任意![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]()
![]() ,
,
故函数![]() 是以1为周期的周期函数. ……………………………………14分
是以1为周期的周期函数. ……………………………………14分
证④:∵函数![]() 是偶函数,即
是偶函数,即![]() =
=![]() ,
,
又函数![]() 是以1为周期的周期函数,即
是以1为周期的周期函数,即![]() =
=![]() ,
,
∴![]() =
=![]()
![]()
![]() =
=![]()
![]()
![]() =
=![]() ,
,
故函数![]() 的图像关于直线
的图像关于直线![]() 对称. …………………14分
对称. …………………14分
(3)∵函数![]() 是偶函数,即求当
是偶函数,即求当![]() 时,所有解之和.
时,所有解之和.
由判断④知当![]() 时有两解,且关于
时有两解,且关于![]() 对称,故其和为413. …20分
对称,故其和为413. …20分