2007学年度(上)新中高级中学期中考试高三数学试卷
(满分150分,考试时间120分钟)
一、填空题(本大题满分44分)本大题共有11题,只要求直接填写结果,每个空格填对得4分,否则一律得零分.![]()
1. 方程 ![]() 的解是
;
的解是
;
2. 方程![]() 的解集为
; 。
的解集为
; 。
3. 已知集合![]() ,
,![]() ,且
,且![]() ,则实数
,则实数![]() 的值是__________;
的值是__________;
4. 若![]() ,且
,且![]() ,则
,则![]() 所在的象限是____________;
所在的象限是____________;
5. 已知正数数列1,![]() 是等差数列, 正数数列
是等差数列, 正数数列![]() 是等比数列,则
是等比数列,则![]() 的值为__________;
的值为__________;
6.不等式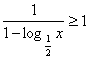 的解集是__________;
的解集是__________;
7. 数列![]() 中,
中,![]() ,又数列
,又数列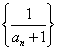 是等差数列,则
是等差数列,则![]() = __________
= __________
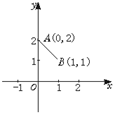
8.设函数y=f(x)是最小正周期为2的偶函数,它在区间[0,1]
上的图象为如图所示的线段AB,则在区间[1,2]上f(x)= ;
9.数列![]() 满足
满足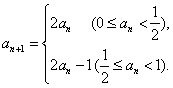 且
且![]() ,则
,则![]()
10.![]() 奇函数,且
奇函数,且![]() 的解集为
的解集为![]() ,
,![]() 的解集为
的解集为![]() 则
则![]() 的解集为_____________;
的解集为_____________;
11. (文)对于实数![]() ,符号
,符号![]() 表示不超过
表示不超过![]() 的最大整数,例如
的最大整数,例如![]() ,
,![]() ,不等式
,不等式![]() 的解集是 ___________ ;
的解集是 ___________ ;
(理)给出定义:若![]() (其中
(其中![]() 为整数),则
为整数),则![]() 叫做离实数
叫做离实数![]() 最近的整数,记作
最近的整数,记作![]() ,即
,即 ![]() . 在此基础上给出下列关于函数
. 在此基础上给出下列关于函数![]() 的四个命题:
的四个命题:
①函数![]() 的定义域是R,值域是[0,
的定义域是R,值域是[0,![]() ];
];
②函数![]() 的图像关于直线
的图像关于直线![]() (k∈Z)对称;
(k∈Z)对称;
③函数![]() 是周期函数,最小正周期是1;
是周期函数,最小正周期是1;
④ 函数![]() 在
在![]() 上是增函数;
其中真命题是___________ ;
上是增函数;
其中真命题是___________ ;
二、选择题(本大题满分16分)本大题共有4题,每题都给出代号为A、B、C、D的四个结论,其中有且只有一个结论是正确的,必须把正确结论的代号写在题后的圆括号内,选对得4分,不选、选错或者选出的代号超过一个(不论是否都写在圆括号内),一律得零分.
12.集合P={(x,y) y=k},Q={(x,y) y=ax+1,a>0且![]() },已知P∩Q只有一个子集,则实数k的取值范围是(A)(-∞,1)
(B)(-∞,1
},已知P∩Q只有一个子集,则实数k的取值范围是(A)(-∞,1)
(B)(-∞,1![]() (C)(1,+∞) (D)(-∞,+∞)
( )
(C)(1,+∞) (D)(-∞,+∞)
( )
13. 等比数列![]() 中,若
中,若![]() ,则
,则![]() 的值为( )
的值为( )
(A)14 (B)16 (C) 18 (D)20 ( )
14. 设a,b,c分别是△ABC的角A,B,C所对的三条边,且![]()
![]() ,则△ABC的面积为
,则△ABC的面积为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]() ( )
( )
15(文)对一切实数![]() ,不等式
,不等式![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是
的取值范围是
A、![]() B、
B、![]() C、
C、![]() D
D ![]() ( )
( )
(理)若不等式![]() 对于任意正整数
对于任意正整数![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是
的取值范围是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]() ( )
( )
三、解答题(本大题满分90分)本大题共有6题,解答下列各题必须写出必要的步骤.
16.(本题满分14分)
已知集合A=![]() ,B=
,B=![]() .
.
⑴当a=2时,求A![]() B;
B;
⑵求使B![]() A的实数a的取值范围.
A的实数a的取值范围.
17. (本题满分12分)
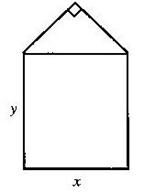 某单位用木料制作如图所示的框架, 框架的下部是边长分别为x、y(单位:m)的矩形.上部是等腰直角三角形. 要求框架围成的总面积8m2. 问x、y分别为多少(精确到0.001m) 时用料最省?
某单位用木料制作如图所示的框架, 框架的下部是边长分别为x、y(单位:m)的矩形.上部是等腰直角三角形. 要求框架围成的总面积8m2. 问x、y分别为多少(精确到0.001m) 时用料最省?
18. (本题满分14分)
设关于x的函数![]() 的最小值为
的最小值为![]() .
.
⑴
写出![]() 的表达式;
的表达式;
⑵试确定能使![]() 的
的![]() 值,并求出此时函数
值,并求出此时函数![]() 的最大值.
的最大值.
19. (本题满分16分)
已知定义在(0,+∞)上的函数f(x)满足①x>1时,f(x)<0;
②f(![]() )=1;③对任意的x、y∈(0,+∞),都有f(xy)=f(x)+f(y),
)=1;③对任意的x、y∈(0,+∞),都有f(xy)=f(x)+f(y),
(1)判断并证明f(x)在(0,+∞)上的单调性;
(2)求f(1), f(2)的值;
(3)求不等式f(x)+f(5-x)≥-2的解集;
20.(本题满分16分) 已知函数![]() ,
,![]() 。
。
(1)试求函数![]() 的反函数
的反函数![]() ;
;
(2)(文)函数![]() ,求
,求![]() 的定义域,判断函数
的定义域,判断函数![]() 的增减性;
的增减性;
(理)函数![]() ,求
,求![]() 的定义域,判断并证明函数
的定义域,判断并证明函数![]() 的增减性;
的增减性;
(3)(文)若(2)中函数![]() 的最小值为3,试求
的最小值为3,试求![]() 的值。
的值。
(理)若(2)中函数![]() ,有
,有![]() 在定义域内恒成立,求
在定义域内恒成立,求![]() 的范围。
的范围。
21.
(本题满分18分) 已知![]()
(1)求![]() 的值;
的值;
(2)若数列![]() 的通项公式为
的通项公式为![]() ,求数列
,求数列![]() 的前100项和
的前100项和![]() ;
;
(3)若数列![]() 的通项公式为
的通项公式为![]() ,且数列
,且数列![]() 的前
的前![]() 项的和为
项的和为![]() ,又
,又![]() :
:![]() ,
, ![]() ;且
;且![]() 若
若![]() 满足对任意不小于2的正整数
满足对任意不小于2的正整数![]() ;都有
;都有![]() 恒成立,试求
恒成立,试求![]() 的最大值。
的最大值。
2007学年度(上)新中高级中学期中考试高三数学试卷(参考答案)
(满分150分,考试时间120分钟)
一、填空题(本大题满分44分)本大题共有11题,只要求直接填写结果,每个空格填对得4分,否则一律得零分.![]()
1. 方程 ![]() 的解是 x=0 ;
的解是 x=0 ;
2. 方程![]() 的解集为
的解集为![]() ;
;
3. 已知集合![]() ,
,![]() ,且
,且![]() ,则实数
,则实数![]() 的值是_____2_____;
的值是_____2_____;
4. 若![]() ,且
,且![]() ,则
,则![]() 所在的象限是____第三象限________;
所在的象限是____第三象限________;
5. 已知正数数列1,![]() 是等差数列, 正数数列
是等差数列, 正数数列![]() 是等比数列,则
是等比数列,则![]() 的值为_____
的值为_____![]() _____;
_____;
6.不等式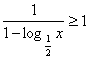 的解集是__
的解集是__![]() ________;
________;
7. 数列![]() 中,
中,![]() ,又数列
,又数列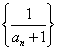 是等差数列,则
是等差数列,则![]() = ___
= ___![]() _______
_______

8.设函数y=f(x)是最小正周期为2的偶函数,它在区间[0,1]
上的图象为如图所示的线段AB,则在区间[1,2]上f(x)= x ;
9.数列![]() 满足
满足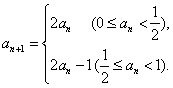 且
且![]() ,则
,则![]()
![]()
10.![]() 奇函数,且
奇函数,且![]() 的解集为
的解集为![]() ,
,![]() 的解集为
的解集为![]() 则
则![]() 的解集为_____
的解集为_____![]() ________;
________;
11. (文)对于实数![]() ,符号
,符号![]() 表示不超过
表示不超过![]() 的最大整数,例如
的最大整数,例如![]() ,
,![]() ,不等式
,不等式![]() 的解集是 _
的解集是 _![]() __________ ;
__________ ;
(理)给出定义:若![]() (其中
(其中![]() 为整数),则
为整数),则![]() 叫做离实数
叫做离实数![]() 最近的整数,记作
最近的整数,记作![]() ,即
,即 ![]() . 在此基础上给出下列关于函数
. 在此基础上给出下列关于函数![]() 的四个命题:
的四个命题:
①函数![]() 的定义域是R,值域是[0,
的定义域是R,值域是[0,![]() ];
];
②函数![]() 的图像关于直线
的图像关于直线![]() (k∈Z)对称;
(k∈Z)对称;
③函数![]() 是周期函数,最小正周期是1;
是周期函数,最小正周期是1;
④ 函数![]() 在
在![]() 上是增函数;
其中真命题是__①___②___③___ ;
上是增函数;
其中真命题是__①___②___③___ ;
二、选择题(本大题满分16分)本大题共有4题,每题都给出代号为A、B、C、D的四个结论,其中有且只有一个结论是正确的,必须把正确结论的代号写在题后的圆括号内,选对得4分,不选、选错或者选出的代号超过一个(不论是否都写在圆括号内),一律得零分.
12.集合P={(x,y) y=k},Q={(x,y) y=ax+1,a>0且![]() },已知P∩Q只有一个子集,则实数k的取值范围是(A)(-∞,1)
(B)(-∞,1
},已知P∩Q只有一个子集,则实数k的取值范围是(A)(-∞,1)
(B)(-∞,1![]() (C)(1,+∞) (D)(-∞,+∞)
( B )
(C)(1,+∞) (D)(-∞,+∞)
( B )
13. 等比数列![]() 中,若
中,若![]() ,则
,则![]() 的值为( )
的值为( )
(A)14 (B)16 (C) 18 (D)20 ( B )
14. 设a,b,c分别是△ABC的角A,B,C所对的三条边,且![]()
![]() ,则△ABC的面积为
,则△ABC的面积为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]() ( C )
( C )
15(文)对一切实数![]() ,不等式
,不等式![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是
的取值范围是
A、![]() B、
B、![]() C、
C、![]() D
D ![]() ( B )
( B )
(理)若不等式![]() 对于任意正整数
对于任意正整数![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是
的取值范围是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]() ( C )
( C )
三、解答题(本大题满分90分)本大题共有6题,解答下列各题必须写出必要的步骤.
16.(本题满分14分)
已知集合A=![]() ,B=
,B=![]() .
.
⑴当a=2时,求A![]() B;
B;
⑵求使B![]() A的实数a的取值范围.
A的实数a的取值范围.
解:⑴![]()
(2)![]()
![]()
![]()
当a<![]() 时,A=(3a+1,2) 要使B
时,A=(3a+1,2) 要使B![]() A,必须
A,必须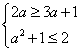 ,此时a=-1;
,此时a=-1;
当a=![]() 时,A=
时,A=![]() ,使B
,使B![]() A的a不存在;
A的a不存在;
当a>![]() 且
且![]() ,时,A=(2,3a+1)要使B
,时,A=(2,3a+1)要使B![]() A,必须
A,必须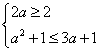 ,此时1<a≤3.
,此时1<a≤3.
综上可知,使B![]() A的实数a的取值范围为[1,3]∪{-1}
A的实数a的取值范围为[1,3]∪{-1}

17. (本题满分12分)
某单位用木料制作如图所示的框架, 框架的下部是边长分别为x、y(单位:m)的矩形.上部是等腰直角三角形. 要求框架围成的总面积8m2. 问x、y分别为多少(精确到0.001m) 时用料最省?
解: xy+![]() x2=8,∴y=
x2=8,∴y=![]() =
=![]() (0<x<4
(0<x<4![]() ).
).
于定, 框架用料长度为
l=2x+2y+2(![]() )=(
)=(![]() +
+![]() )x+
)x+![]() ≥4
≥4![]() .
.
当(![]() +
+![]() )x=
)x=![]() ,即x=8-4
,即x=8-4![]() 时等号成立.
时等号成立.
此时,
x≈2.343,y=2![]() ≈2.828.
≈2.828.
故当x为2.343m,y为2.828m时, 用料最省.
18. (本题满分14分)
设关于x的函数![]() 的最小值为
的最小值为![]() .
.
(1)写出![]() 的表达式;
的表达式;
⑵试确定能使![]() 的
的![]() 值,并求出此时函数
值,并求出此时函数![]() =
=![]() 的最大值.
的最大值.
解:(1)f(x)=2(cosx-)2--2a-1。
当a≥2时,则cosx=1时,f(x)取最小值,即g(a)=1-4a;
当-2<a<2时,则cosx=时,f(x)取最小值,即g (a)=--2a-1;
当a≤-2时,则cosx=-1时,f(x)取最小值,即g (a)=1
综上所述:g (a)=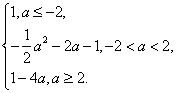
(2)若g (a)=,a只能在[-2,2]内。
解方程--2a-1=,得a=-1,和a=-3。因-1∈[-2,2],故a=-1为所求,此时
f(x)=2(cosx+)2+;当cosx=1时,f(x)有最大值5。
19. (本题满分16分)
已知定义在(0,+∞)上的函数f(x)满足①x>1时,f(x)<0;
②f(![]() )=1;③对任意的x、y∈(0,+∞),都有f(x y)=f(x)+f(y),
)=1;③对任意的x、y∈(0,+∞),都有f(x y)=f(x)+f(y),
(1)判断并证明f(x)在(0,+∞)上的单调性;
(2)求f(1), f(2)的值;
(3)求不等式f(x)+f(5-x)≥-2的解集;
解:(1)任取x1、x2∈(0,+∞)且x1>x2,则![]() >1.
>1.
f(x1)=f(![]() ·x2)=f(
·x2)=f(![]() )+f(x2),
)+f(x2),
∴f(x1)-f(x2)=f(![]() )<0.
)<0.
∴f(x)在(0,+∞)上为减函数.
(2)f(1)=f(1)+f(1),则f(1)=0.
又∵f(1)=f(2)+f(![]() )=f(2)+1=0.
)=f(2)+1=0.
∴f(2)=-1.∴f(4)=2f(2)=-2.
(3)原不等式等价于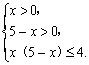
![]()
20.(本题满分16分) 已知函数![]() ,
,![]() 。
。
(1)试求函数![]() 的反函数
的反函数![]() ;
;
(2)(文)函数![]() ,求
,求![]() 的定义域,判断函数
的定义域,判断函数![]() 的增减性;
的增减性;
(理)函数![]() ,求
,求![]() 的定义域,判断并证明函数
的定义域,判断并证明函数![]() 的增减性;
的增减性;
(3)(文)若(2)中函数![]() 的最小值为3,试求
的最小值为3,试求![]() 的值。
的值。
(理)若(2)中函数![]() ,有
,有![]() 在定义域内恒成立,求
在定义域内恒成立,求![]() 的范围。
的范围。
解:(1)易求![]() 。
。
(2)(文)![]() ,
,
![]() 时,定义域为
时,定义域为![]() ;
;![]() 时,定义域为
时,定义域为![]() ;
;
此函数在定义域内单调递增(∵![]() 与
与![]() 在公共定义域内均为增函数,∴它们的和也为增函数)。
在公共定义域内均为增函数,∴它们的和也为增函数)。
(理)作差证明(略)
(3)(文)当![]() 时,由
时,由![]() ;
;
当![]() 时,由
时,由![]() 。 ∴所求的
。 ∴所求的![]() 的值为
的值为![]() 或
或![]() 。
。
(理)当![]() 时,由
时,由![]()
![]() 。
。
当![]() 时,由
时,由![]()
![]() 。
。
∴![]() 的取值范围是
的取值范围是![]() 。
。
21.
(本题满分18分) 已知![]()
(1)求![]() 的值;
的值;
(2)若数列![]() 的通项公式为
的通项公式为![]() ,求数列
,求数列![]() 的前100项和
的前100项和![]() ;
;
(3)若数列![]() 的通项公式为
的通项公式为![]() ,且数列
,且数列![]() 的前
的前![]() 项的和为
项的和为![]() ,又
,又![]() :
:![]() ,
, ![]() ;且
;且![]() 若
若![]() 满足对任意不小于2的正整数
满足对任意不小于2的正整数![]() ;都有
;都有![]() 恒成立,试求
恒成立,试求![]() 的最大值。
的最大值。
解:(1)![]() =
=![]()
(2)![]()
![]()
![]()
![]()
![]()
![]()
(3)![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,
![]() m
m![]()
![]()