2007年全国名校考创新最后冲刺模拟卷
数学（文理） 2007.4
本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。共150分。考试时间120分钟。
第Ⅰ卷（选择题 共60分）
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。
1．
（ ）
A．–2 –i B．–2 +i C．2 –i D．2 + i
2．若奇函数f ( x ) ( x∈R)满足f ( 2 ) = 1 , f ( x + 2 ) = f ( x ) + f ( 2 )，则f ( 5 ) = （ ）
A．0 B．1 C．
D．5
3．（理）球O的截面把垂直截面的直径分成1
：3 两部分，若截面半径为
，则球O的体积为（ ）
A．16
B．
C．
D．
（文）已知直径m⊥平面
，直线
平面
，则下列命题正确的是（ ）
A．若∥, 则m⊥n B．若⊥, 则m∥n
C．若m⊥n , 则∥ D．若n∥, 则∥
4．集合P = {x , 1} , Q = {y
, 1, 2 }， 其中x , y∈{1 , 2 , 3 , … , 9 }，且PQ。把满足上述条件的一对有序整数对( x、y )作为一个点的坐标，则这样的点的个数是（ ）
A．9个 B．14 C．15 D．21个
5．下列函数中周期为2的是（ ）
A．y =
2cos2x –1 B．y =
sin2x + cos2x
C．y =
tan (
) D．y = sin xcos x
6．（理）如果复数z = a2 – a –2 + (a2 –3a + 2 ) i 为纯虚数，那么实数a的值为（ ）
A．1 B．2 C．–2 D．1或–2
（文）若等比数列{an }的前n项和为Sn , 且S1 = 18 , S2 = 24 , 则S4 =（ ）
A．
B．
C．
D．
7．P为曲线
=1的右支上一点，M、N分别是圆 ( x + 5 )2 + y2
= 4和( x –5
)2 = y2 = 1上的点，则PM – PN 的最大值为（ ）
A．6 B．7 C．8 D．9
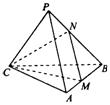8．四面体P—ABC中，M为棱AB的中点，则PA与CM所成角的余弦值为（ ）
A．
B．
C．
D．
9．抛物线y2 = 4x ，按向量a平移后所得抛物线的焦点坐标为（3，2），则平移后的抛物线的顶点坐标为（ ）
A．4，2 B．2，2 C．–2，–2 D．2，3
|
~N ( 2 , a2 ),且P (2＜＜4 ＝ = 0.4，则P
的值为（ ）
A．0.3 B．0.1 C．0.4 D．以上均不对
（文）在100个产品中，一等品20个，二等品30个，三等品50个，用分层抽样的方法抽取一个量为20的样本，则二等品中产品A被抽取到的概率（ ）
A．等于
B．等于
C．等于
D．不确定
11若f ( x ) = log
x , A = f(
), G = f (
), H = f (
) , a、b为实数，则A、G、H的大小关系为（ ）
A．A≥G≥H B．A≥H≥G C．H≥G≥A D．G≥H≥A
12．如果关于x的方程 ( 2–x–2 )2 – a –2 = 0有实数a的取值范围是（ ）
A．
B．
C．
D．
第Ⅱ卷（非选择题 共90分）
二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上。
13．若△ABC的内角A满足sin 2A
=
,则cos A – sin A = _________
|
|
|
|
|
|
，N =
，且M、N都是集合
|
|
的“长度”，那么集合M∩N的“长度的最小值为________
15．已知函数f ( x ) =
,那么f ( 1 ) + f ( 2 ) + f ( 3
) + f ( 4 ) + f (
) + f (
) + f (
) = _____
16．（理）已知函数y = f ( x ) = x3 + px2 + qx 的图象与x轴切于非原点的一点，且y极小 = – 4 ,
那么p + q的值为 _______ .
（文）若 tan (
) =
,则tan 2的值是______
三、解答题：本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤。
17．（本题满分12分）
已知函数f
( x ) =
（Ⅰ）求函数f ( x )的最小正周期；
（Ⅱ）求函数f ( x )取得最大值的所有x组成的集合。
18．（本题满分12分）
设等差数列{an}的前n项和为Sn，若a3 = 12 , S12＞0，S13＜0，请指出S1 , S2 … ，S12中哪个最大？说明理由。
19．（本题满分12分）
如图所示，PD垂直于正方形ABCD所在的平面，AB =2， E是PB的中点，
与
夹角的余弦值为。
（Ⅰ）建立适当的坐标系，写出点E的坐标；
（Ⅱ）在平面PAD内求上一点F，使EF⊥平面PCB 。
20．（本小题满分13分）
已知二次函数f ( x ) = x2 + 2bx + c ( b , c∈R)，满足f ( 1 ) = 0 , 且关于x的方程f ( x ) + x + b = 0的两个实数根分别在区间（–3，–2）、（0，1）内。
（Ⅰ）求实数b的取值范围；
（Ⅱ）（理）若函数F ( x ) = logbf ( x ) 在区间 (–1 – c , 1 – c )具有单调性，求实数c的取值范围。
|
|
，求实数b、c的值。
21．（本题满分12分）
|
|
,1 ) , b = ( 1 , cos ) , 
（Ⅰ）若a⊥b，求；
（Ⅱ）求 a + b 的最大值。
22．（本题满分13分）
（理）已知抛物线方程为y =
x2 + h , 点A、B三点都在抛物线上，且直线PA、PB的倾斜角互为补角。
（Ⅰ）求证：向量
与
共线；
（Ⅱ）若直线AB经过点（0，1），试在抛物线上求一点Q，使Q在直线AB上方，且△QAB的面积为最大。
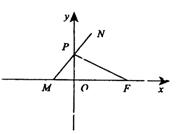
（文）如图所示，点F( a , 0 )( a＞0 )，点P在y轴上运动，M在x轴上，N为动点，且
·
=0，
=0。
（Ⅰ）求点N的轨迹C的方程；
（Ⅱ）过点F( a , 0 )的直线l（不与x轴垂直）与曲线C交于A、B两点，设点K (– a,0 ) ,
与
的夹角为，求证：0＜＜
参考答案
1．C 2．C 3．（理）C （文）A 4．B 5．C
6．（理）C （文）A 7．D 8．B 9．B 10．（理）B （文）A
11．A 12．D
13．
14．
15．
16．（理）15 （文）
17．（Ⅰ）f ( x ) =
=
+ 1 = 
=2sin
+1 = 2sin
+1
∴函数f (
x )的最小值周期为T =
（Ⅱ）当f ( x )取最大值时，sin=1.此时有2x –
= 2k+即x = k+
(k
∈Z) ∴所求x的集合为
[点评]此题是对三角函数知识的考查。
18．设等差数列的首项为a1,公差为d。
|
|
|
|
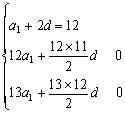解得
Sn
= na1 +
=
又d＜0，所以
最小时，最大。
又由
＜d＜3，可得6＜
＜6.5
故当n = 6时，Sn最大，S1，S2，…，S12中S6最大。
[点评]从函数的角度观察、分析数列问题，开辟了数列问题求解的新天地，给我们一个全新的视角。
19．（Ⅰ）以DA、DC、DP所在直线分别为x轴、y轴、z轴，建立空间直角坐标系，设P
（0，0，2m），（m＞0）。
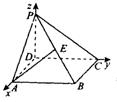则A（2，0，0）、B（2，2，0）、C（0，2，0）
E（1，1，m），从而=（–1，1，m），
=（0，0，2m），cos
=
得m = 1,所以E点的坐标为（1，1，1）
（Ⅱ）由于点F在平面PAD内，故可设F点坐标为 ( x , 0 , z )，由
⊥平面PCB得：
·
= 0，即
( x –1 , –1, z –1 )·( 2 , 0 , 0 ) = 0
x = 1·(x –1 , –1 , z –1 )·( 0, 2 ,
2
) = 0z = 0
所以点E的坐标为 ( 1 , 0 , 0 ), 即点F是DA的中点时，可耻下场使EF⊥平面PCB 。
[点评]对平面上存在一点的问题，一般情况下思维量和运算量比较大，通过对空间图形的理解，寻找面的特殊性，巧妙构建坐标，将使问题更加简单。
20．（Ⅰ）由题知, f ( 1 ) = 1 + 2b + c = 0 ,∴c = –1 –2b
记g ( x ) = f ( x ) + x + b = x2 + ( 2b + 1 )x + b + c = x2 + ( 2b + 1 )x – b –1
|
|
|
|
|
|
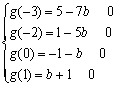
即b∈(,
)
（Ⅱ）（理）令a = f ( x ) , ∵0＜＜b＜＜1
∴logbu在区间（0，+∞）上是减函数。
而 –1 – c = 2b＞– b , 函数f ( x ) = x2 + 2bx + c 的对称轴为x = 1– b ,∴f ( x ) 在区间( –1
– c , 1 – c )上单调递增
从而函数F ( x ) = logbf ( x )在区间 ( –1 – c ,1 – c ) 上为减函数。
且f ( x )在区间( –1 – c ,1 – c )上恒有f ( x )＞0
只需要f ( –1 – c )≥0
|
|
|
|
|
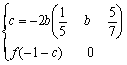
（文）由题知x1 = –1 , x2 = 1是方程x2 + 2bx + c = 0的两个根由韦达定理得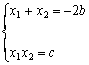
[点评]函数类题目是每年高考考查的重点内容。
21．（Ⅰ）a⊥b，则sin+cos= 0
由此得tan= –1(
＜＜＝
所以=
（Ⅱ）由a
= (sin , , 1 ) , b = ( 1 , cos )得
a + b
= (sin+1 , 1 + cos)
a + b =
=
=
当sin (+
) = 1时， a + b 取得最大值，即当=时， a + b 的最大值为
。
22．（理）（Ⅰ）把点P的坐标（2，4）公共秩序抛物线方程，得h = 6，所以抛物线方程为
y =
设PA的斜率为k，则PB的斜率为 – k
又设A ( x1 , y1 ) , B ( x2 , y2 )
直线PA ：y – 4 = k ( x –2 )
由①②消去y，得x2 + 2kx – 4k + 4 = 0
设其二根为x1和x2所以A 点横坐标为 x1 = –2k –2
将 – k换成k，得B点横坐标为x2 = 2k –2
∴kAB =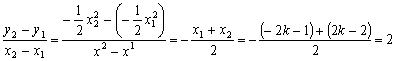
而kOP =
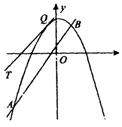所以AB∥OP，即向量与共线
（Ⅱ）如右图，作抛物线的切线QT∥AB，Q为切点，Q到AB的
距离最大，所以△QAB的面积为最大，即切点Q ( x0 , y0 ) 为所求
，对y =求y′= – x
, ∵
= kAB = 2
∴–x0 = 2
即x0 = –2 ，从而y0 = 4 . 即所求点Q的坐标为 ( –2 , 4 )
（文）（Ⅰ）设N ( x , y ) , M ( x0 , 0 ) , P ( 0 , y0 )
则= (x0 , – y0 ) . 
= ( x , y – y0 )
由·=0得ax0 +
=0 ①
由+= 0，得( x + x0 , y – 2y0
) = 0
即
∴
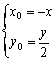
代入①得，y2 = 4ax 即为所求。
（Ⅱ）设l方程为y
= ( x – a ) , 由
消去x，得
y2
–
=0
设A (x1 , y1 ) , B ( x2 , y2 ) , 则y1y2 = – 4a2
= ( x1 + a , y1 )
, = ( x2 + a , y2 )
·= ( x1 + a ) ( x2
+ a ) + y1y2 = x1x2
+ a ( x1 + x2 ) + a2
+ y1y2
=
+a2 – 4a2
=
＞
∴cos=
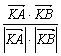＞0
∴0＜＜
[点评]理科题（Ⅰ）是解析几何与向量的综合，求证向量与共线就是求证AB∥OP，以下思路明确，但有计算上的难点。解决这个难点的方法是“灯比计算”，如上解法，先求点A (x1,y1)的横坐标x1的公式，类比地得到x2，直至求得kAB .本题之。
（Ⅱ）有几种初等解法，但都没有上面的导数法简捷，还要注意：数形结合始终是本题思路的主线，向量及其运算是新课程的新增内容，由于向量融数、形于一体，具有代数形式和几何形式的双重身份，使它成为中学数学知识的一个交点，成为联系多项内容的媒介。