2006—2007学年度北京市东城区综合练习（二）
高 三 数 学（文科）
本试题分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.共150分，考试时间120分钟.考试结束，将本试卷和答题卡一并交回。
第Ⅰ卷（选择题，共40分）
注意事项：
1．答第I卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2．每小题选出答案后，用铅笔把答题卡对应题目的答案标号涂黑。如需改动，用橡皮
擦干净后，再选涂其它答案，不能答在试卷上。
一、选择题：本大题共8小题，每小题5分，共40分。在每题列出的四个选项中，选出符合题目要求的一项。
1．已知向量a=(3，－4)，b=(5，2)，则向量a+b等于 （ ）
A．（2，6） B．（6，2） C．（8，－2） D．（－8，2）
2．若抛物线
的焦点与椭圆
的左焦点重合，则p的值为 （ ）
A．－2 B．2 C．－4 D．4
3．若集合A={3，a2}B={2，4}则“a=2”是“A∩B、{4}”的 （ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
4．记函数y=1+2－x的反函数为y=g(x)，则g(5)等于 （ ）
A．2 B．－2 C．－4 D．4
5．五名同学解答5道不同的数学题，每名同学解答1道题，其中甲不能解答第1题，则不
同的解答方案共有 （ ）
A．
种 B．
种 C．
种 D．
种
6．已知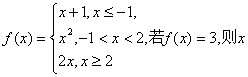
的值是 （ ）
A．2 B．2或
C．±
D．
|
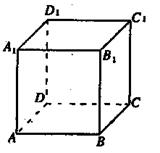
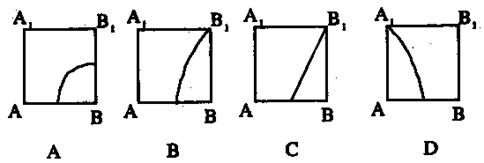
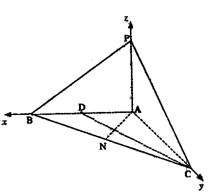
A1ABB1内一动点，且点P到A1A和BC的距
离相等，则P点的轨迹是下国科中的（ ）
|
8．若
，例如：
（ ）
A．是奇函数不是偶函数 B．是偶函数不是奇函数
C．即是奇函数又是偶函数 D．即不是奇函数又不是偶函数
第Ⅱ卷（共110分）
注意事项：
1．用钢笔或圆珠笔直接答在试题卷上。
2．答卷前将密封线内项目填写清楚。
二、填空题：本大题共6小题，每小题5分，共30分。把答案填在题中横线上。
|
10．已知等差数列{an}的公差为2，若a1，a3，a4成等比数列，则a2= .
11．
的展开式中，常数项为 .（用数字作答）
12．一个与球心距离为2的平面截球所得的圆面面积为4π，则球的体积V= .
13．已知x,y满足条件
y的最大值为8，则k= .
14．定义一种运算“*”，它对于整数n满足以下运算性质：
（1）2*1001=1；（2）（2n+2）*1001=3·[（2n）*1001]，则2008*1001的值是 .
三、解答题：本大题共6小题，共80分。解答应写出文字说明，证明过程或演算步骤。
15．（本小题共13分）
已知函数f(x)=x3－2ax2+6bx的图象与直线15x+y－4=0相切，切点为（1，－11）.
（Ⅰ）求a，b的值；
（Ⅱ）求函数f(x)的单调递减区间.
|
16．（本小题共13分）
△ABC的三个内角A，B，C所对的边分别是a，b，c，向量m=（sinB，1－cosB）， n=（sinB，cosB），且m·n=0.
（Ⅰ）求cosB的值；
（Ⅱ）求证：b2≥3ac.
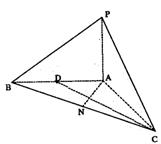
17．（本小题共14分）
|
.
（Ⅰ）求证：PB⊥AC；
（Ⅱ）求异面直线CD与PB所成角的大小；
（Ⅲ）求点A到平面PBC的距离.
|
18．（本小题共13分）
经统计，某校教工食堂一个售饭窗口每天中午排队买饭的教工人数及相应的概率如下：
| 排队人数 | 0—5 | 6—10 | 11—15 | 16—20 | 21—25 | 25人以上 |
| 概率 | 0.1 | 0.15 | 0.25 | 0.25 | 0.2 | 0.05 |
（Ⅰ）每天中午不超过20位教工排队买饭的概率是多少？
（Ⅱ）一周5个工作日中，若有3天或3天以上中午出现超过15位教工排队买饭的概率
大于0.80，学校就需要增加售饭窗口，请问该学校是否需要增加售饭窗口？
19．（本小题共13分）
已知双曲线
的离心率
（Ⅰ）求双曲线C的方程；
（Ⅱ）若直线
与双曲线C恒有两个不同的交点A和B，且
，
求k的取值范围.
20．（本小题共14分）
已知数列{an}中，前n项和为Sn，点（an+1，Sn+1）在直线y=4x－2，其中n=1，2，3……，
（Ⅰ）设bn=an+1－2an，且a1=1，求证数列{bn}是等比数列；
（Ⅱ）令f(x)=b1x+b2x2+…+bnxn，求函数f(x)在点x=1处的导数f′(1)并比较f′(1)与
6n2－3n的大小.
参考答案
一、选择题（本大题共8小题，每小题5分，共40分）
1.C 2.D 3.A 4.B 5.B 6.D 7.B 8.B
|
9.
10.－6 11.－20 12. 
13.－6 14. 31003
注：两个空的填空题填对一个得3分.
三、解答题（本大题共6小题，共80分）
15．（本小题共13分）
解：（I）
………………………………2分
由于f(x)的图象与直线15x+y－4=0相切于点（1，－11），
所以
…………………………………………4分
即
解得a=3，b=－1.………………………………………………7分
（II）由
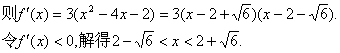
故函数f(x)的单调递减区间是
.……………………13分
16．（本小题共13分）
解：（I）∵m=(sinB,1－cosB), n=(sinB,cosB),
又m·n=0，
∴sin2B+cosB－cos2B=0.
∴2cos2B－cosB－1=0.……………………………………3分
解得cosB=－
或cosB=1（舍）.
∵0<B<π，
∴cosB=－.…………………………………………7分
（II）由（I）可知cosB=－，
∴
.
即b2=a2+c2+ac.…………………………………………11分
又∵a2+c2≥2ac,
∴b2≥3ac.………………………………………………13分
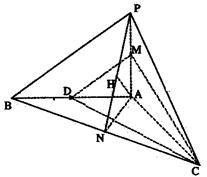
17．（本小题共14分）
解法一：
（I）∵AN⊥BC，且AN=BN=CN=，
∴AB=AC且AB⊥AC.…………………………2分
∵PA⊥平面ABC，
∴AB是PB在平面ABC内的射影.
∵PB⊥AC.…………………………………………5分
（II）取PA的中点M，连结DM，CM，则DM//PB.
∴∠CDM是异面直线CD与PB所成的角.……7分
|
在△CDM中，
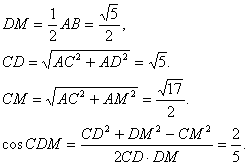
所以异面直线CD与PB所成角的大小为arccos
.……………………9分
（III）连结PN.
∵PA⊥平面ABC，
又由已知可得CN⊥平面PAN，
∴平面PAN⊥平面ABC.
过A点作AH⊥PN于H，
则AH⊥平面PBC.
∴AH的长就是点Ａ到平面PBC的距离.……………………………………11分
由已知可得BC=2.
∵PA⊥平面ABC.
∴PA⊥AN.
又PN=
，
在Rt△PAN中，
有
|
.…………………………14分
解法二：
（I）∵AN⊥BC，
且AN=BN=CN=,
∴AB=AC且AB⊥AC.
以A为原点，AB，AC，AP
分别为x、y、z轴建立空间直角坐标系.
则有P（0，0，1），B（2， 0，0），
C（0，2，0），D（1，0，0），A（0，0，0）.
=（2，0，－1），
=（0，2，0），
·=2×0+0×2+（－1）×0=0.
∴⊥.
∴PB⊥AC.……………………………………6分
（II）
=（1，－2，0），
设异面直线CD与PB所成的角为θ.
.
所以异面直线CD与PB所成角的大小为arccos.……………………10分
（III）设平面PBC的法向量为
.
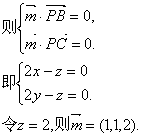
则点A到平面PBC的距离为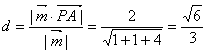
.……14分
18．（本小题满分13分）
解：（I）设每天不超过20位教工排队买饭的概率为p：
p=0.1+0.15+0.25+0.25=0.75.
即不超过20位教工排队买饭的概率为0.75.……………………5分
（II）每天中午超过15位教工排队买饭的概率为0.25+0.05+0.2=；
一周5个工作日中，没有出现中午超过15位教工排队买饭的概率为： 
；
一个周5个工作日中，恰有一天中午出现超过15位教工排队买饭的概率为：
；
一个周5个工作日中，恰有二天中午出现超过15位教工排队买饭的概率为：
.
所以有3天或3天以上中午出现超过15位教工排队买饭的概率为：
19．（本小题共13分）
解：（I）由已知
，
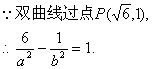
又c2=a2+b2，
可解得 a2=3，b2=1.
所求双曲线C的方程为
………………………………6分
（II）将
由直线l与双曲线交于不同的两点得
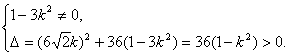
即
①……………………………………8分
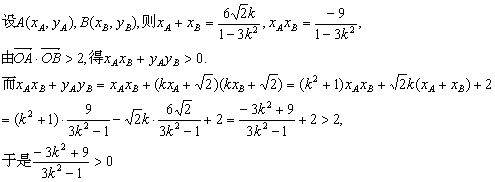
可得
. ②…………………………………………11分
由①，②得
.
故k的取值范围为
.………………………………13分
20．（本小题共14分）
解：（I）由已知点（an+1，Sn+1）在直线y=4x－2上.
∴Sn+1=4(an+1)－2.
即Sn+1=4an+2.(n=1，2，3，…)
∴Sn+2=4an+1+2.
两式相减，得Sn+2－Sn+1=4an+1－4an.
即an+2=4an+1－4an.……………………………………3分
an+2－2an+1=2(an+1－2an).
∵bn=an+1－2an，（n=1，2，3，…）
∴bn+1=2bn.
由S2=a1+a2=4a1+2，a1=1。
解得a2=5，b1=a2－2a1=3.
∴数列{bn}是首项为3，公式为2的等比数列.……………………6分
（II）由（I）知bn=3·2n－1，
∵f(x)=b1x+b2x2+…+bnxn，
∴f′(x)=b1+2b2x+…+nbnxn－1.
从而f′(1)=b1+2b2+…+nbn
=3+2·3·2+3·3·22+…+n·3·2n－1
=3(1+2·2+3·22+…+n·3·2n－1)………………………………8分
设Tn=1+2·2+3·22+…+n·2n－1，
2Tn=2+2·22+3·23+…+（n－1）·2n－1+n·2n.
两式相减，得－Tn=1+2+22+23+…+2n－1－n·2n
=
.
∴Tn=(n－1)·2n+1.
∴f′(1)=3(n－1)·2n+3.……………………………………11分
由于f′(1)－(6n2－3n)=3[(n－1)·2n+1－2n2+n]
=3(n－1)[2n－(2n+1)].
设g(n)= f′(1) －(6n2－3n).
当n=1时，g(1)=0，∴f′(1) =6n2－3n；
当n=2时，g(2)= －3<0，∴f′(1)<6n2－3n；
当n≥时，n－1>0，又2n=(1+1)n=
≥2n+2>2n+1，
∴(n－1)[2n－(2n+1)]>0，即g(n)>0,从而f′(1)>6n2－3n.…………14分