2006—2007学年度北京市东城区综合练习（二）
高 三 数 学（理科）
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分。考试时间120分钟。考试结束，将本试卷和答题卡一并交回。
第Ⅰ卷（选择题 共40分）
注意事项：
1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其它答案标号。不能答在试卷上。
一、选择题：本大题共8小题。每小题5分，共40分。在每小题列出的四个选项中，选出符合题目要求的一项。
1．在复平面内，复数
对应的点位于 （ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
2．若集合
，则“
”是“
”的 （ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
3．设函数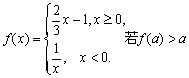
，则实数a的取值范围是 （ ）
A．
B．
C．
D．（0，1）
4．某小组有6名女生，8名男生，这14名同学排成一行，其中A，B，C，D四名女生必须排在一起，另两名女生不相邻且不与前4名女生相邻，则不同的排法共有 （ ）
A．
种 B．
种 C．
种 D．
种
5．斜率为2的直线l过双曲线
的右焦点，且与双曲线的左、右两支分别相交，则双曲线的离心率e的取值范围 （ ）
A．
B．
C．
D．
|
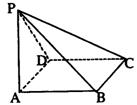
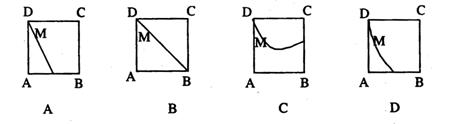
ABCD为正方形，侧面PAD⊥底面ABCD，M为底面ABCD
内的一个动点，且满足MP=MC，则点M在正方形ABCD内
的轨迹为 （ ）
|
|
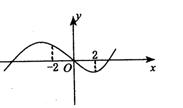
7．函数
的图象如图所示，
则
的值一定 （ ）
|
C．小于0 D．小于或等于0
8．若
，例如：
（ ）
A．是奇函数不是偶函数 B．是偶函数不是奇函数
C．即是奇函数又是偶函数 D．即不是奇函数又不是偶函数
第Ⅱ卷（共110分）
注意事项：
1．用钢笔或圆珠笔直接答在试题卷上。
2．答卷前将密封线内项目填写清楚。
二、填空题：本大题共6小题，每小题5分，共30分。把答案填在题中横线上。
9．已知等差数列{an}的公差为2，若a1，a3，a4成等比数列，则a2= .
10．在二项式
的展开式中，若所有项的系数之和等于64，那么n = .
|
11．函数
的反函数
.
12．已知函数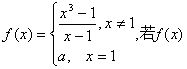
在R上连续，则a = ，此时
.
13．已知点P(x,y)满足条件
y的最大值为8，则k= .
14．定义一种运算“*”，它对于整数n满足以下运算性质：
（1）2*1001=1；（2）（2n+2）*1001=3·[（2n）*1001]，则2008*1001的值是 .
三、解答题：本大题共6小题，共80分。解答应写出文字说明，证明过程或演算步骤。
15．（本小题共13分）
设函数
相切于点A，且点A的横坐标为1.
（Ⅰ）求a，b的值；
（Ⅱ）求函数f(x)的单调区间，并指出在每个区间上的增减性.
16．（本小题共13分）
已知△ABC的三个内角分别为A，B，C，向量
夹角的余弦角为
（Ⅰ）求角B的大小；
（Ⅱ）求
的取值范围.
17．（本小题共14分）
|
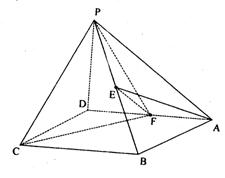
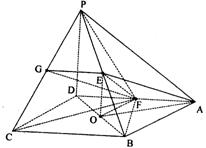
（Ⅰ）求异面直线PD一AE所成角的大小；
（Ⅱ）求证：EF平面PBC；
（Ⅲ）求二面角F—PC—B的大小.
|
18．（本小题共13分）
某学生玩投飞镖游戏，他一次投镖所得环数m的概率分布如下：
| m | 8 | 9 | 10 |
| p | 0.5 | 0.3 | 0.2 |
若这名学生投两次飞镖，记两次投中的最高环数为ξ.
（Ⅰ）求该名学生两次都投中8环的概率；
（Ⅱ）求ξ的分布列和数学期望Eξ.
19．（本小题共13分）
已知双曲线
的右焦点是F，右顶点是A，虚轴的上端点是B，且
|
（Ⅰ）求双曲线C的方程；
（Ⅱ）过点P(0,4)的直线l，交双曲线C于M、N两点，交x轴于点Q（点Q与双曲线C 的顶点不重合），当
时，求点Q的坐标.
20．（本小题共14分）
已知函数
图象上的两点，横坐标为
的点P满足
（O为坐标原点）.
（Ⅰ）求证：
为定值；
（Ⅱ）若
；
（Ⅲ）已知
的前n项和，若
都成立，试求m的取值范围.
参考答案
|
1．C 2．A 3．B 4．C 5．D 6．A 7．B 8．B
二、填空题：本大题共6小题，每小题5分，共30分。把答案填在题中横线上。
9．－6 10．6 135 11．
12．3 3 13．－6 14．31003
注：两个空的填空题对一个得3分。
三、解答题（本大题共6小题，共80分）
15．（本小题共13分）
解：（Ⅰ）
…………2分
由于f(x)的图象与直线
相切于点A，点A的横坐标为1，
则
所以
…………………………………………………………………………4分
即
…………………………………………………7分
（Ⅱ）由
，
……………………………………… 9分
令
；
令
故函数
上分别单调递增，
在区间
上单调递减 …………………………………………………………13分
16．（本小题满分13分）
解：（Ⅰ）
………………………………………………………2分
即
解得
（舍）
……………………………………………………………………………6分
（Ⅱ）由（Ⅰ）可知
…… 9分
，
|
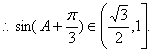
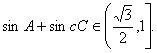…………………………………………………………13分
17．（本小题共14分）
解法一：
（Ⅰ）连结BD
∵PD⊥平面ABCD，
∴平面PDB⊥平面ABCD，
过点E作EO⊥BD于O，连结AO.
则EO∥PD，且EO⊥平面ABCD.
∴∠AEO为异面直线PD，AE所成的角…………3分
∵E是PB的中点，
则O是BD的中点，
且EO=PD=1.
在Rt△EOA中，AO=
，
.
即异面直线PD与AE所成角的大小为
……………………………… 5分
（Ⅱ）连结FO，
∵F是AD的中点，
∴OF⊥AD.
∵EO⊥平面ABCD，
由三垂线定理，得EF⊥AD.
又∵AD∥BC，
∴EF⊥BC. …………………………………………………………………………… 7分
连结FB.
可求得FB = PF =
则EF⊥PB.
又∵PB∩BC = B，
∴EF⊥平面PBC. ……………………………………………………………………10分
（Ⅲ）取PC的中点G，连结EG，FG.
则EG是FG在平面PBC内的射影
∵PD⊥平面ABCD， ∴PD⊥BC
又DC⊥BC，且PD∩DC = D，
∴BC⊥平面PDC，
∴BC⊥PC，
∵EG∥BC，
则EG⊥PC
∴FG⊥PC
∴∠FGE是二面角F—PC—B的平面角 …………………………………………12分
在Rt△FEG中，EG=BC = 1，GF = 
，
∴二面角F—PC—B的大小为
解法二：
|
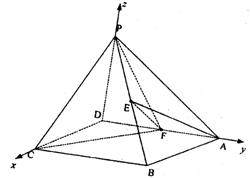
A（0，2，0），B（2，2，0），C（2，0，0），
D（0，0，0），P（0，0，2），E（1，1，1）……2分
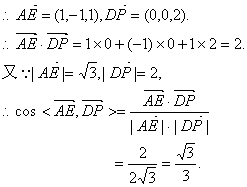
故异面直线AE与DP所成角的大小为
………………………………6分
（Ⅱ）
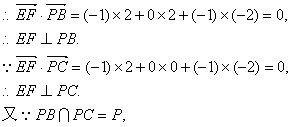
∴EF⊥平面PBC. ……………………………………………………………………10分
（Ⅲ）设平面PFC的法向量为
则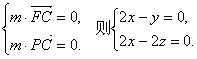
令
由（Ⅱ）知平面PBC的法向量为
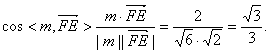
则二面角F—PC—B的大小为为 ……………………………………14分
18．（本小题共13分）
解：（Ⅰ）设该名学生两次都投中8环的概率为P，
则P = 0.52 = 0.25.
即该名学生两次都投中8环的概率为0.25.
（Ⅱ）ξ的可能取值为8，9，10
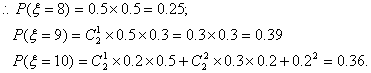
故ξ的分布列为：
| ξ | 8 | 9 | 10 |
| P | 0.25 | 0.39 | 0.36 |
…………………………9分
ξ的数学期望
Eξ= 8×0.25 + 9×0.39 +10×0.36 = 9.11 ………………………………………………13分
19．（本小题满分13分）
解：（Ⅰ）由条件知
① ……………………………2分
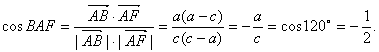
② ………………………………………………………………………4分
解①，②得
则
故双曲线C的方程为
……………………………………………………6分
（Ⅱ）由题意知直线l的斜率k存在且不等于零，
设l的方程为：
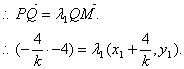
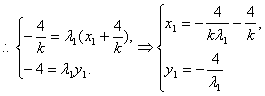……………………………………8分
在双曲线C上，
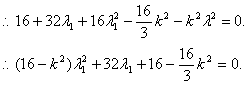
同理
…………………………………………11分
若
，则直线l过项点，不合题意，∴
的两根
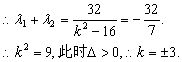
∴所求Q点的坐标为
…………………………………………………………13分
20．（本小题共14分）（Ⅰ）证：由已知可得，
，
∴P是MN的中点，有x1 + x2 = 1.
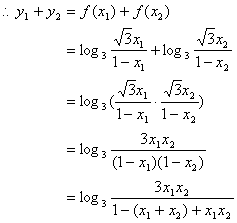
……………………………………………………5分
（Ⅱ）解：由（Ⅰ）知当
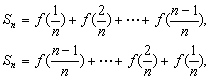
相加得
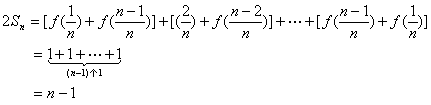
…………………………………………………………………………10分
（Ⅲ）解：当
时，
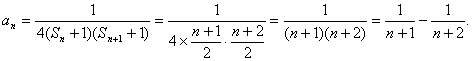
又当n = 1时，
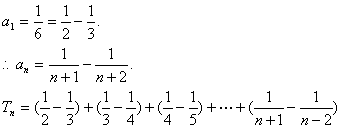
…………………………………………………………………………12分
由于都成立，
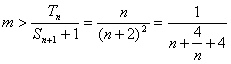
，当且仅当n = 2时，取“=”，
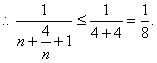
因此
综上可知，m的取值范围是
………………………………………………14分