崇文区2006-2007学年度第二学期高三统一练习(二)
数 学(文科) 2007.5
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至9页,共150分。考试时间120分钟。考试结束,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题共 40分)
注意事项:
1.答第一卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮
擦干净后,再选涂其他答案标号。不能答在试卷上。
一、本大题共8小题,每小题5分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
(1)![]() 的值是( )
的值是( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(2)若![]() 是等差数列
是等差数列![]() 的前
的前![]() 项和,且
项和,且![]() ,
,![]() ,则( )
,则( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(3)“![]() ”是“直线
”是“直线![]() 与直线
与直线![]() 平行且不重合”的 ( )
平行且不重合”的 ( )
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(4)若![]() ,且
,且![]() ,则
,则![]() 与
与![]() 的夹角为( )
的夹角为( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(5)在![]() 这六个数字组成的没有重复数字的四位数中,偶数共有( )
这六个数字组成的没有重复数字的四位数中,偶数共有( )
(A)156个 (B)108个
(C) 96 个 (D) 84个
(6)对于直线![]() 、
、![]() 和平面
和平面![]() 、
、![]() 、
、![]() ,则在下列条件中,可判断平面
,则在下列条件中,可判断平面![]() 与
与![]() 平行的是( )
平行的是( )
(A)![]() 、
、![]() 都垂直于平面
都垂直于平面![]()
(B)![]() 内存在不共线的三点到
内存在不共线的三点到![]() 的距离相等
的距离相等
(C)![]() 、
、![]() 是
是![]() 内两条直线,且
内两条直线,且![]() ,
,![]()
 (D)
(D)![]() 、
、![]() 是两条异面直线,且
是两条异面直线,且![]() ,
,![]() ,
,![]() ,
,![]()
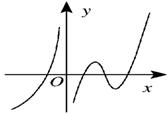
(7)设函数![]() 在定义域内可导,
在定义域内可导,![]() 的图象如右图所示,
的图象如右图所示,
则导函数![]() 的图象可能是( )
的图象可能是( )
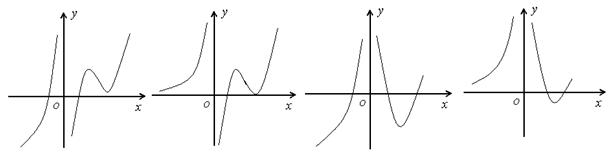
(A) (B) (C) (D)
(8)设定义在![]() 上的函数
上的函数![]() 满足
满足![]() 当
当![]() 时,
时,![]() ;
;![]()
![]() ;
;
![]() 当
当![]() 时,
时,![]() ,则在下列结论中:①
,则在下列结论中:①![]() ;②
;②![]() 在
在![]() 上是递减函数;
上是递减函数;
③存在![]() ,使
,使![]() ; ④若
; ④若![]() ,则
,则![]() .
.
正确结论的个数是 ( )
(A)1个 (B)2个
(C)3个 (D)4个
崇文区2006-2007学年度第二学期高三统一练习(一)
数 学(文科)
第II卷(共110分)
注意事项:
1. 用钢笔或圆珠笔将答案直接写在试卷上。
2. 答卷前将密封线内的项目填写清楚。
| 题号 | 二 | 三 | 总分 | |||||
| 15 | 16 | 17 | 18 | 19 | 20 | |||
| 分数 | ||||||||
| 得分 | 评卷人 |
二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中
横线上.
(9)双曲线![]() 的渐近线方程是_________.
的渐近线方程是_________.
(10)在900个零件中,有一级品400个,二级品300个,三级品200个,现采用分层抽样抽
取容量为45的样本,那么一级品,二级品,三级品抽取的个数分别为______.
(11) 若球![]() 的半径为2,球面上有两点
的半径为2,球面上有两点![]() ,且
,且![]() ,则
,则![]() 两点间的球面距离为
两点间的球面距离为
_____.
(12)在![]() 的展开式中,常数项是_____(用数字作答).
的展开式中,常数项是_____(用数字作答).
(13)已知实数![]() 满足不等式组
满足不等式组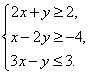 则
则![]() 的最大值等于_____,
的最大值等于_____,
 最小值等于_____.
最小值等于_____.
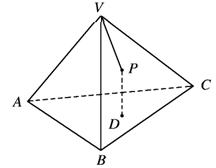
(14)已知![]() 是正四面体
是正四面体![]() 的面
的面![]() 上一点,
上一点,
点![]() 到平面
到平面![]() 距离与到点
距离与到点![]() 的距离相等,
的距离相等,
则动点![]() 的轨迹为_____.
的轨迹为_____.
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
| 得分 | 评卷人 |
(15)(本小题满分13分)
甲、乙两台雷达独立工作,在一段时间内,甲台雷达发现飞行目标的概率为![]() ,乙台雷达发现飞行目标的概率为
,乙台雷达发现飞行目标的概率为![]() ,计算在这段时间内,
,计算在这段时间内,
(Ⅰ)甲、乙两台雷达均未发现目标的概率;
(Ⅱ)至多有一台雷达发现目标的概率.
| 得分 | 评卷人 |
(16)(本小题满分13分)
已知![]() .
.
(Ⅰ)求![]() 的单调递增区间;
的单调递增区间;
(Ⅱ)在![]() 中,角
中,角![]() 、
、![]() 、
、![]() 的对边分别是
的对边分别是![]() 、
、![]() 、
、![]() ,满足
,满足![]() ,
,
求函数![]() 的取值范围.
的取值范围.
| 得分 | 评卷人 |
(17)(本小题满分13分)
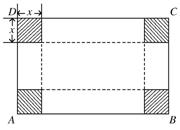 如图,
如图,![]() 是一块矩形铁板
是一块矩形铁板![]() ,剪掉四个阴影部分的小正方形,沿虚线折叠后,焊接成一个无盖的长方体水箱.
,剪掉四个阴影部分的小正方形,沿虚线折叠后,焊接成一个无盖的长方体水箱.
(Ⅰ)写出水箱的容积![]() 与水箱高度
与水箱高度![]() 的函数表达式,并求其定义域;
的函数表达式,并求其定义域;
(Ⅱ)当水箱高度![]() 为何值时,水箱的容积
为何值时,水箱的容积![]() 最大,并求出其最大值.
最大,并求出其最大值.
| 得分 | 评卷人 |
(18)(本小题满分13分)
直四棱柱![]() 中,
中,![]() ,
,![]() 为等边三角形, 且
为等边三角形, 且![]() .
.
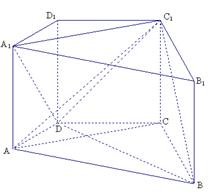 (Ⅰ)求
(Ⅰ)求![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)设![]() 是
是![]() 上的点,当
上的点,当![]() 为何值时,
为何值时,![]() 平面
平面![]() ?并证明你的结论.
?并证明你的结论.
| 得分 | 评卷人 |
(19)(本小题满分13分)
已知抛物线![]() :
:![]() 的焦点与椭圆
的焦点与椭圆![]() :
:![]() 的右焦点
的右焦点![]() 重合,
重合,![]() 是椭圆的左焦点.
是椭圆的左焦点.
(Ⅰ) 在![]() 中,若
中,若![]() ,
,![]() ,点
,点![]() 在抛物线
在抛物线![]() 上运动,求
上运动,求![]() 重心
重心![]() 的轨
的轨
迹方程;
(Ⅱ) 若![]() 是抛物线
是抛物线![]() 与椭圆
与椭圆![]() 的一个公共点,且
的一个公共点,且![]() ,求
,求![]()
的值及![]() 的面积.
的面积.
| 得分 | 评卷人 |
(20)(本小题满分13分)
设![]() 为数列
为数列![]() 的前
的前![]() 项和,且
项和,且![]()
![]() 数列
数列![]() 的通项公式为
的通项公式为![]()
![]()
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若将数列![]() 与
与![]() 的公共项按它们在原来数列中的先后顺序排成一个新数列
的公共项按它们在原来数列中的先后顺序排成一个新数列![]() ,证明数列
,证明数列![]() 的通项公式为
的通项公式为![]() .
.
崇文区2006---2007学年度第二学期高三统一练习(二)
数学(文科)试题参考答案及评分标准 2007.5
一、选择题(本大题共8小题,每小题5分,共40分)
(1)(C)(2)(A )(3)(C )(4)(C )(5)(A )(6)(D)(7)(D)(8)(B)
二、填空题(本大题共6小题,每小题5分,共30分)
(9)![]() (10)
(10)
![]() (11)
(11)![]() (12)7 (13)13,
(12)7 (13)13,![]() (14)椭圆一部分
(14)椭圆一部分
三、解答题(本大题共6小题,共80分)
(15)(共13分)
解:设这段时间内“甲台雷达发现飞行目标”为事件![]() ;“乙台雷达发现飞行目标”为事件
;“乙台雷达发现飞行目标”为事件![]() .
.
(Ⅰ)![]() 甲、乙两台雷达均未发现目标,即事件
甲、乙两台雷达均未发现目标,即事件![]() 发生,
发生,
∴甲、乙两台雷达均未发现目标的概率为
![]()
![]() .-----------------------------------5分
.-----------------------------------5分
答:甲,乙两台雷达均未发现目标的概率为0.015.
(Ⅱ) ![]() 至多有一台雷达发现目标,即事件
至多有一台雷达发现目标,即事件![]() 发生.
发生.
∴![]()
![]()
![]()
![]() .
.
答:至多有一台雷达发现目标的概率为![]() .---------------------------------------------13分
.---------------------------------------------13分
(16)(共13分)
解:(Ⅰ)由![]()
![]() .
.
∵![]() ,(
,(![]() )
)
∴![]() ,(
,(![]() )
)
∴![]() 的单调递增区间为
的单调递增区间为![]() (
(![]() ).------------------------6分
).------------------------6分
(Ⅱ) 由![]() ,
,
得![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,且
,且![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ,
,![]() ,
,
故函数![]() 的取值范围是
的取值范围是![]() .----------------------------------------------------------13分
.----------------------------------------------------------13分
(17)(共13分)
解:(Ⅰ)由题意得 ![]()
![]() .--------------------------------------------4分
.--------------------------------------------4分
(Ⅱ) ∵![]() ,
,
∴![]() ,
,
令![]() ,即
,即![]() ,
,
解得,![]() 或
或![]() (舍).
(舍).
当![]() 变化时,
变化时,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
| + |
|
|
|
|
| 最大值 |
|
由上表可知,当![]() 时,容积
时,容积![]() 有最大值,且最大值为
有最大值,且最大值为![]() 立方厘米.
立方厘米.
--------------------------------------------------------------------13分
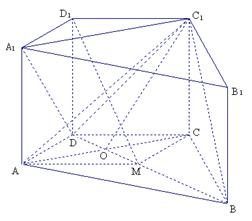 (18)(共14分)
(18)(共14分)
解:(Ⅰ)∵![]() 是直四棱柱,
是直四棱柱,
∴![]() ,且
,且![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
即![]() (或其补角)是
(或其补角)是![]() 与
与![]() 所成的角.
所成的角.
连接![]() ,在三角形
,在三角形![]() 中,
中,![]() ,
,![]() ,
,
∴![]()
![]() .
.
故![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .------------------------------------5分
.------------------------------------5分
(Ⅱ)设![]() ,则
,则![]() ,连接
,连接![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() 为
为![]() 在平面
在平面![]() 内的射影,
内的射影,
∴![]() ,
,
则![]() 为二面角
为二面角![]() 的平面角.
的平面角.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
故二面角![]() 的大小为
的大小为![]() .-----------------------------------10分
.-----------------------------------10分
(Ⅲ)在![]() 上取点
上取点![]() ,使得
,使得![]() ,连接
,连接![]() ,
,
∵![]() ,
,
又![]() ,且
,且![]() ,
,
∴![]() ,
,
∴四边形![]() 是一个正方形.
是一个正方形.
可证![]() ,又
,又![]() ,
,
∴![]() 平面
平面![]() ,此时
,此时![]() .
.
故当![]() 时,有
时,有![]() 平面
平面![]() .--------------------------------------------------14分
.--------------------------------------------------14分
(19)(共13分)
解:(Ⅰ)设重心![]() ,
,![]() .
.
则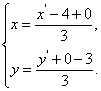 整理得
整理得 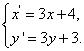 (
(![]() )
)
将(![]() )代入
)代入![]() 中,得
中,得![]()
所以,![]() 重心
重心![]() 的轨迹方程为
的轨迹方程为![]() --------------------6分
--------------------6分
(Ⅱ) ∵椭圆与抛物线有共同的焦点,由![]() 得
得![]() ,
,
∴![]() 椭圆方程为
椭圆方程为![]() .
.
设![]() ,由
,由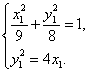 得
得 ![]()
∴![]() (舍).
(舍).
∵![]() 是
是![]() 的准线,即抛物线的准线过椭圆的另一个焦点
的准线,即抛物线的准线过椭圆的另一个焦点![]() ,
,
设点![]() 到抛物线
到抛物线![]() 准线的距离为
准线的距离为![]() ,则
,则![]() .
.
又![]() ,
,
∴![]() ,
, ![]() .
.
过点![]() 作
作![]()
![]() 轴,垂足为
轴,垂足为![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() ∴
∴![]() .
.
∴![]() .--------------------------------------13分
.--------------------------------------13分
(20)(共14分)
解:(Ⅰ)∵![]()
![]()
∴![]() ,
,
∴![]()
当![]() ≥2时,
≥2时,![]()
∴![]() 即
即![]()
![]() ≥2
≥2![]() .
.
∴数列![]() 是以3首项,公比为3的等比数列,
是以3首项,公比为3的等比数列,![]()
∴![]() -------------------------------------------------------------6分
-------------------------------------------------------------6分
证明(Ⅱ)由(Ⅰ)知![]() 、
、![]() 显然不是数列
显然不是数列![]() 中的项.
中的项.
∵![]()
∴![]() 是数列
是数列![]() 中的第6项,
中的第6项,
设![]() 是数列
是数列![]() 中的第
中的第![]() 项,则
项,则![]()
![]() 、
、![]() .
.
∵![]()
![]() ,
,
∴![]() 不是数列
不是数列![]() 中的项.
中的项.
∵![]() ,
,
∴![]() 是数列
是数列![]() 中的项.
中的项.
∴![]() ,
,
∴数列![]() 的通项公式是
的通项公式是![]() .----------------------------------------14分
.----------------------------------------14分