高2007届第二轮复习质量检测试题(2007.4.10)
数 学(理科) ![]()
本卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试用时120分钟.
第Ⅰ卷(选择题 共50分)
一、选择题:(本大题共10小题,每小题5分,共50)各题答案必需答在答题卡上。
1.已知等差数列![]() 中,
中,![]() ,则
,则![]() 的值是 ( )
的值是 ( )
A.15 B.30 C.31 D.64
2.设复数![]() 在( )
在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.函数![]() 有极值的充要条件是( )
有极值的充要条件是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.函数![]() 的一个单调递减区间是 ( )
的一个单调递减区间是 ( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D. ![]()
5.若![]() ,那么
,那么![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.设![]() 为互不重合的平面,l,m,n为互不重合的直线,给出下列四个命题:
为互不重合的平面,l,m,n为互不重合的直线,给出下列四个命题:
① 若![]() 则
则![]() ∥
∥![]() ;② 若
;② 若![]() ∥
∥![]() ∥
∥![]() ,则
,则![]() ∥
∥![]() ;
;
③ 若![]() ∥
∥![]() 则
则![]() ∥
∥![]() ; ④ 若
; ④ 若![]() ∥
∥![]() 则m∥n.
则m∥n.
其中真命题的个数是( )
A.1 B.2 C.3 D.4
7.设椭圆的中心在原点O,右焦点为F,右准线为l,如果在l上存在点M,使线段OM的垂直平分线经过F,则椭圆的离心率的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.若随机变量![]() 为( )
为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
| |
A.16 B.18 C.20 D.无数个
10.已知M、N是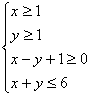 所围成的区域内的不同两点,则
所围成的区域内的不同两点,则![]() 的取值范围是( )
的取值范围是( )
A.![]() 0,2
0,2![]() B.
B.![]() 0,
0,![]()
![]() C.
C.![]() 0,
0,![]()
![]() D.[0,
D.[0,![]() ]
]
第Ⅱ卷(非选择题 共100分)
二、填空题:(本大题共6小题,每小题4分,共24分) 把答案填写在答题卡相应位置上.
11.若椭圆![]() 的离心率为
的离心率为![]() ,则λ等于___________
,则λ等于___________
12.![]() 的展开式的常数项是-20,则
的展开式的常数项是-20,则![]()
13.设离散型随机变量![]() 可能的取值为1、2、3、4,
可能的取值为1、2、3、4,![]() (
(![]() ),又
),又![]() 的数学期望为
的数学期望为![]() ,则
,则![]() ___________
___________
14.设集合![]() ,映射,
,映射,![]() 满足:
满足:![]() ,则这样的映射共有____________个
,则这样的映射共有____________个
15.已知![]() ,记
,记![]()
![]()
![]() ,则
,则![]() _________
_________
16.已知数列![]() 满足:
满足:![]() ,定义使
,定义使![]() 为整数的
为整数的![]() 叫“期盼数”,则区间
叫“期盼数”,则区间![]() 内所有的期盼数的和
内所有的期盼数的和![]()
三、解答题:(本大题共6小题,共76分)解答应写出文字说明、证明过程或演算步骤.
17.(13分)在△![]() 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为![]() 、
、![]() 、
、![]() 且满足
且满足![]()
(1)求角![]() 的大小;
的大小;
(2)向量![]()
![]() ,向量
,向量![]()
![]() ,求
,求![]() ·
·![]() 的最小值.
的最小值.
18.(13分)已知![]() 为数列
为数列![]() 的前
的前![]() 项和,且
项和,且![]() ,n=1,2,3…
,n=1,2,3…
(1)求证: 数列![]() 为等比数列;
为等比数列;
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
19.(13分)设A、B是两个平面区域,面积分别为![]() 、
、![]() ,且
,且![]() ,则区域A内的随机点落在区域B内的概率
,则区域A内的随机点落在区域B内的概率![]() .则称这样的概率模型为几何概型. 现有两人相约7点到8点在某地会面,先到者等候另一人20分钟,过时离去. 求两人能够会面的概率.
.则称这样的概率模型为几何概型. 现有两人相约7点到8点在某地会面,先到者等候另一人20分钟,过时离去. 求两人能够会面的概率.
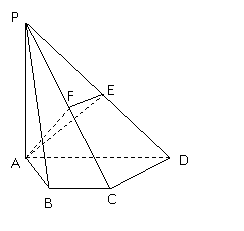
20.(13分)如图,四棱锥P-ABCD的底面ABCD是梯形,![]() 平面ABCD,BC//AD,AB=CD,
平面ABCD,BC//AD,AB=CD,
![]() ,
,![]() ,点E,F分别在棱PD,PC上,且满足
,点E,F分别在棱PD,PC上,且满足![]() .
.
(1)求证:EF//平面ABCD;
(2)当![]() 时,求AE与平面PAC所成的角的正切值;
时,求AE与平面PAC所成的角的正切值;
(3)是否存在![]() ,使平面AEF
,使平面AEF![]() 平面PCD?若存在,求出
平面PCD?若存在,求出![]() 的值; 若不存在,说明理由.
的值; 若不存在,说明理由.
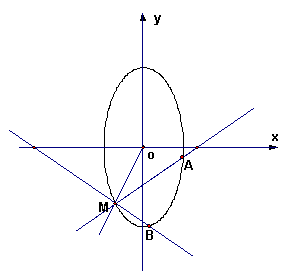 21.(12分)已知椭圆方程为
21.(12分)已知椭圆方程为![]() ,射线
,射线![]() 与椭圆的交点为
与椭圆的交点为![]() 过
过![]() 作倾斜角互补的两条直线,分别与椭圆交于
作倾斜角互补的两条直线,分别与椭圆交于![]() 两点(异于
两点(异于![]() ).
).
(1)求证: 直线![]() 的斜率
的斜率![]() 为定值;
为定值;
(2)求△![]() 面积的最大值。
面积的最大值。
22.(12分)设![]() 是
是![]() 的一个极值点,
的一个极值点,
(1) 求![]() 与
与![]() 的关系式(用
的关系式(用![]() 表示
表示![]() )并求
)并求![]() 的单调区间.
的单调区间.
(2)是否存在实数![]() ,使得对任意
,使得对任意![]() 及
及![]() 总有
总有![]()
![]() 恒成立,若存在求出
恒成立,若存在求出![]() 的范围。若不存在,说明理由.
的范围。若不存在,说明理由.
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | C | C | A | C | B | B | D | B | C |
二、填空题:
11. 3 12.![]() 13.
13.![]()
14. 35 15. —1
16.解: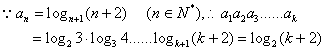
要使![]() 为正整数,可设
为正整数,可设
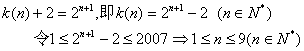

17.解:(1)由![]() 得
得![]()
即![]()
又∵![]() ∴
∴![]() ∴
∴![]() 又
又![]() 故
故![]()
(2)∵![]() 又∵
又∵![]() ∴
∴![]() ,
,![]() ∴
∴![]() ≤
≤![]()
又∵![]() ·
·![]()
![]() ∴
∴![]() ·
·![]() 的最小值为
的最小值为![]()
18. (Ⅰ)解:![]()
![]() ,
,
![]() .
.
![]() .
.
![]() 是以2为公比的等比数列
是以2为公比的等比数列
(Ⅱ)![]() ,
,![]()
![]() .
.
![]() .
.
当![]() 为偶数时,
为偶数时,
![]()
![]()
![]()
![]() ;
;
当![]() 为奇数时,
为奇数时,
![]() n=
n=![]() .
.
综上,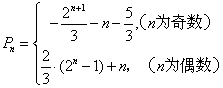
19. 解:设两人到达的时间分别为7点到8点之间的x分钟、y分钟.用![]() 表示每次试验的结果,则所有可能结果为:
表示每次试验的结果,则所有可能结果为:
![]() ;
;
记两人能够会面为事件A,则事件A的可能结果为:
![]() .
.
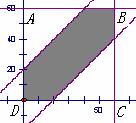
如图所示,试验全部结果构成区域Ω为正方形ABCD. 而事件A所构成区域是正方形内两条直线![]() ,
,![]() 所夹中间的阴影部分. 根据几何概型公式,得到:
所夹中间的阴影部分. 根据几何概型公式,得到:
 .
.
所以,两人能够会面的概率为![]() .
.
20.解:(1)证:![]()
又![]() ,
,![]()
(2)![]() 是等腰梯形, 又
是等腰梯形, 又![]()
设![]() ,则
,则![]() ,
,![]()
![]() ,
,![]()
又![]() 平面ABCD,
平面ABCD,![]() ,
,![]() 平面
平面![]()
又![]() ,
,![]() 平面
平面![]() ,
,![]() 是AE与平面
是AE与平面![]() 所成角.
所成角.
又![]() ,
,![]() 是PD的中点,且
是PD的中点,且![]()
又![]() ,在
,在![]() 中,
中,![]() .
.
(3)当![]() 时, 平面AEF
时, 平面AEF![]() 平面PCD.
平面PCD.
![]()
![]() 平面ABCD,
平面ABCD,![]() ,
,
在![]() 中,由(2)知,
中,由(2)知,![]() ,
,
若![]() ,则
,则![]()
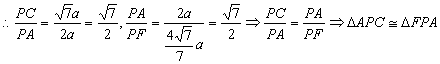
![]() ,而
,而![]() ,
,
又![]() 则
则![]()
![]() ,即
,即![]() 时,平面AEF
时,平面AEF![]() 平面PCD.
平面PCD.
21.解(1)∵ 斜率 ![]() 存在,不妨设
存在,不妨设![]() >0,求出
>0,求出 ![]() (
(![]() ,
, ![]() ).
).
直线 ![]() 方程为
方程为![]() ,直线
,直线 ![]() 方程
方程 ![]()
分别与椭圆方程联立,可解出![]() ,
,![]()
∴ ![]() .
.
∴ ![]() .
.
(2)设直线AB方程为![]() ,与
,与![]() 联立,消去y得
联立,消去y得
![]()
![]() .
.
由 ![]() >0得-4<
>0得-4< ![]() <4,且
<4,且 ![]() ≠0,
≠0,
点![]() 到
到 ![]() 的距离为
的距离为![]() .
.
![]()
设△![]() 的面积为S. ∴
的面积为S. ∴ ![]() .
.
当![]() 时,得
时,得![]() .
.
22.解(1)![]()
由![]() 得
得![]() ∴
∴![]()
![]()
令![]() 得
得![]()
由于![]() 是
是![]() 的极值点,故
的极值点,故![]() ,即
,即![]()
①
当![]() 时,
时,![]() ,故
,故![]() 为
为![]() 的单调增区间;
的单调增区间;![]() 为
为![]() 的单调减区间。
的单调减区间。
②
当![]() 时,
时,![]() ,故
,故![]() 为
为![]() 的单调增区间;
的单调增区间;![]() 为
为![]() 的单调减区间。
的单调减区间。
(2)由![]() 得
得![]() ,从而知
,从而知![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,![]() 的值域为
的值域为![]()
假设存在实数![]() 满足题设,依题意有:
满足题设,依题意有:
![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
令![]() ,则有
,则有
![]() ,解得
,解得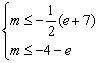 ,即
,即![]()
注:[也可通过分离变量![]() 求解(从略)] 故存在实数
求解(从略)] 故存在实数![]() 满足题设。
满足题设。