江西5校2008届高三07年8月开学联考
![]() 数学试题 组卷:韩丰
数学试题 组卷:韩丰
考生注意:本试卷共22小题,满分150分,答题时长120分钟。请把你的解答按要求填写在答题卷的相应位置,否则不能得分。
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1、某个命题与正整数![]() 有关,若
有关,若![]() 时该命题成立,那么可推得
时该命题成立,那么可推得![]() 时该命题也成立,现在已知当
时该命题也成立,现在已知当![]() 时该命题不成立,那么可推得
时该命题不成立,那么可推得
A.当![]() 时,该命题不成立
B.当
时,该命题不成立
B.当![]() 时,该命题成立
时,该命题成立
C.当![]() 时,该命题不成立
D.当
时,该命题不成立
D.当![]() 时,该命题成立
时,该命题成立
2、已知向量![]() ≠
≠![]() ,
,![]() =1,对任意t∈R,恒有
=1,对任意t∈R,恒有![]() -t
-t![]() ≥
≥![]() -
-![]() ,则
,则
A.![]() ⊥
⊥![]() B.
B.![]() ⊥(
⊥(![]() -
-![]() ) C.
) C.![]() ⊥(
⊥(![]() -
-![]() ) D.(
) D.(![]() +
+![]() )⊥(
)⊥(![]() -
-![]() )
)
| |
3、如图所示是2008年北京奥运会的会徽,其中的“中国印” 主体 由四个互不连通的色块构成,可以用线段在不穿越其他色块的条件下将其中任意两个色块连接起来(如同架桥),如果用三条线段将这四个色块连接起来,不同的连接方法共有
A.8种 B.12种
C.16种 D.20种
4、设函数![]() 的最大值为3,则f(x)的图象的一条对称轴的方程是
的最大值为3,则f(x)的图象的一条对称轴的方程是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5、已知正整数![]() 满足
满足![]() ,使得
,使得![]() 取最小值时,则实数对(
取最小值时,则实数对(![]() 是( )
是( )
A.(5,10) B.(6,6) C.(10,5) D.(7,2)
6、已知直线![]() 、
、![]() ,平面
,平面![]() 、
、![]() ,给出下列命题:
,给出下列命题:
①若![]() ,且
,且![]() ,则
,则![]() ②若
②若![]() ,且
,且![]() ,则
,则![]()
③若![]() ,且
,且![]() ,则
,则![]() ④若
④若![]() ,且
,且![]() ,则
,则![]()
其中正确的命题是
![]() .①③
.①③ ![]() .②④
.②④ ![]() .③④
.③④ ![]() .①
.①
7、点O为△ABC内一点,且存在正数![]() ,设△AOB,△AOC的面积分别为S1、S2,则S1:S2=
,设△AOB,△AOC的面积分别为S1、S2,则S1:S2=
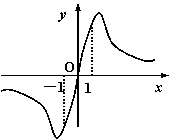 A.λ1:λ2 B.λ2:λ3
A.λ1:λ2 B.λ2:λ3
C.λ3:λ2 D.λ2:λ1
8、若函数![]() 的图象如图所示,则m的范围为
的图象如图所示,则m的范围为
A.(-∞,-1) B.(-1,2)
C.(1,2) D.(0,2)
9、设![]() , 则对任意正整数
, 则对任意正整数![]() , 都成立的是
, 都成立的是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10、设定义域为R的函数![]() 都有反函数,且函数
都有反函数,且函数![]() 和
和![]() 图象关于直线
图象关于直线![]() 对称,若
对称,若![]() ,则
,则![]() (4)为
(4)为
A. 2002 B. 2004 C. 2007 D. 2008
11、从一块短轴长为2b的椭圆形玻璃镜中划出一块面积最大的矩形,其面积的取值范围是[3b2,4b2],则这一椭圆离心率e的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12、已知![]()
A.-4 B.8 C.0 D.不存在
二、填空题:本大题共4小题,每小题4分,共16分。
13、复数![]() 的虚部为____________.
的虚部为____________.
14、已知![]() ,若
,若![]() 恒成立,则
恒成立,则![]() 的最大值为
。
的最大值为
。
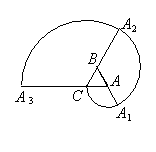 15、如图,一条螺旋线是用以下方法画成:ΔABC是边长为1的正三角形,曲线CA1,A1A2,A2A3分别以A、B、C为圆心,AC、BA1、CA2为半径画的弧,曲线CA1A2A3称为螺旋线。旋转一圈.然后又以A为圆心AA3为半径画弧…,这样画到第n圈,则所得螺旋线的长度
15、如图,一条螺旋线是用以下方法画成:ΔABC是边长为1的正三角形,曲线CA1,A1A2,A2A3分别以A、B、C为圆心,AC、BA1、CA2为半径画的弧,曲线CA1A2A3称为螺旋线。旋转一圈.然后又以A为圆心AA3为半径画弧…,这样画到第n圈,则所得螺旋线的长度![]() .(用π表示即可)
.(用π表示即可)
16、设{x}表示离x最近的整数,即若![]() ≤
≤![]() (m∈Z),则{x} = m.给出下列关于函数
(m∈Z),则{x} = m.给出下列关于函数![]() 的四个命题:
的四个命题:
①函数![]() 的定义域是R,值域是[0,
的定义域是R,值域是[0,![]() ];
];
②函数![]() 的图像关于直线
的图像关于直线![]() (k∈Z)对称;
(k∈Z)对称;
③函数![]() 是周期函数,最小正周期是1;
是周期函数,最小正周期是1;
④函数![]() 是连续函数,但不可导.
是连续函数,但不可导.
其中真命题是 __________ .
三、解答题:本大题共6小题,共74分。
17、(本小题满分12分)
已知向量![]() ,函数
,函数![]() .
.
(I)若![]() ,求函数
,求函数![]() 的值;
的值;
(II)将函数![]() 的图象按向量c=
的图象按向量c=![]() 平移,使得平移后的图象关于原点对称,求向量c.
平移,使得平移后的图象关于原点对称,求向量c.
|
| 数学 | |||||
| 5 | 4 | 3 | 2 | 1 | ||
| 英语 | 5 | 1 | 3 | 1 | 0 | 1 |
| 4 | 1 | 0 | 7 | 5 | 1 | |
| 3 | 2 | 1 | 0 | 9 | 3 | |
| 2 | 1 |
| 6 | 0 |
| |
| 1 | 0 | 0 | 1 | 1 | 3 | |
18、(本小题满分12分)下表为某班英语及数学成绩的分 布.学生共有50人,成绩分1~5五个档次.例如表中所示英语成绩为4分、数学成绩为2分的学生为5人.将全班学生的姓名卡片混在一起,任取一枚,该卡片同学的英语成绩为![]() ,数学成绩为
,数学成绩为![]() 。设
。设![]() 为随机变量(注:没有相同姓名的学生)
为随机变量(注:没有相同姓名的学生)
(I)![]() 的概率为多少?
的概率为多少?![]() 的概率为多少?
的概率为多少?
(II)![]() 等于多少?当
等于多少?当![]() 的期望为
的期望为![]() 时,试确定
时,试确定![]() ,
,![]()
的值 .
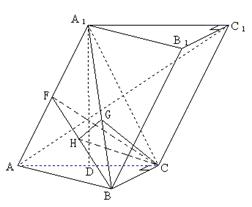
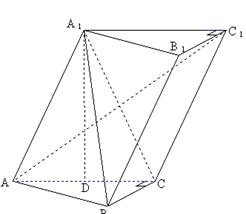 19、已知斜三棱柱
19、已知斜三棱柱![]() ,
,![]() ,
,![]() ,
,![]() 在底面
在底面![]() 上的射影恰为
上的射影恰为![]() 的中点
的中点![]() ,又知
,又知![]() 。
。
(I)求证:![]() 平面
平面![]() ;
;
(II)求![]() 到平面
到平面![]() 的距离;
的距离;
(III)求二面角![]() 的大小。
的大小。
20、(本小题满分12分)设数列![]()
(I)求数列{bn}的通项公式;
(II)若存在实数t,使得数列![]() 成等差数列,记数列
成等差数列,记数列![]() 的前n项和为Tn.证明:
的前n项和为Tn.证明:![]()
21、(本小题满分12分)已知圆![]() 上的动点,点Q在NP上,点G在MP上,且满足
上的动点,点Q在NP上,点G在MP上,且满足![]() .
.
(I)求点G的轨迹C的方程;
(II)过点(2,0)作直线![]() ,与曲线C交于A、B两点,O是坐标原点,设
,与曲线C交于A、B两点,O是坐标原点,设![]() 是否存在这样的直线
是否存在这样的直线![]() ,使四边形OASB的对角线相等(即OS=AB)?若存在,求出直线
,使四边形OASB的对角线相等(即OS=AB)?若存在,求出直线![]() 的方程;若不存在,试说明理由.
的方程;若不存在,试说明理由.
22、(本小题满分14分)已知函数![]()
(I)求f(x)在[0,1]上的极值;
(II)若对任意![]() 成立,求实数a的取值范围;
成立,求实数a的取值范围;
(III)若关于x的方程![]() 在[0,1]上恰有两个不同的实根,求实数b的取值范围.
在[0,1]上恰有两个不同的实根,求实数b的取值范围.
江西5校2008届高三07年8月开学联考参考答案
1C 2B 3C 4A 5A 6D 7C 8C 9C
![]()
![]()
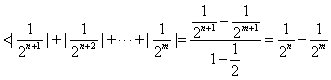
![]() . 故应选C .
. 故应选C .
10D 11A 12B
13、-1 ; 14、![]() 。提示:由已知,
。提示:由已知,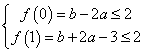 ,即
,即![]() ,由线性规划知识知,当
,由线性规划知识知,当![]() ,
,![]() 时
时![]() 达到最大值
达到最大值![]() 。
。
15,解析: ![]()
![]() .
.
16、①②③④
三、解答题:
17,解:由题意,得![]()
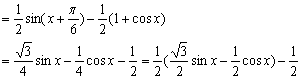
![]() ………………………………………………………………5分
………………………………………………………………5分
(1)![]() ,
,
![]() …………………………………7分
…………………………………7分
(2)由图象变换得,平移后的函数为![]() ,
,
而平移后的图象关于原点对称,![]() ,………………9分
,………………9分
即![]() ,
,
即![]() .………………………………………………………………12分
.………………………………………………………………12分
18,(1)![]() ;--------6分
;--------6分
(2)![]()
![]() ①;---------9分
①;---------9分
又![]()
![]() ②; - --------11分
②; - --------11分
结合①②可得![]() ,
,![]() .
---------12分
.
---------12分
 19.解:(I)因为
19.解:(I)因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
得![]() ,又
,又![]()
所以![]() 平面
平面![]() ;……………4分
;……………4分
(II)因为![]() ,所以四边形
,所以四边形![]() 为
为
菱形,
故![]() ,又
,又![]() 为
为![]() 中点,知
中点,知![]() 。
。
取![]() 中点
中点![]() ,则
,则![]() 平面
平面![]() ,从而面
,从而面![]() 面
面![]() ,
,
过![]() 作
作![]() 于
于![]() ,则
,则![]() 面
面![]() ,
,
在![]() 中,
中,![]() ,故
,故![]() ,
,
即![]() 到平面
到平面![]() 的距离为
的距离为![]() 。……………8分
。……………8分
(III)过![]() 作
作![]() 于
于![]() ,连
,连![]() ,则
,则![]() ,
,
从而![]() 为二面角
为二面角![]() 的平面角,
的平面角,
在![]() 中,
中,![]() ,所以
,所以![]() ,
,
在![]() 中,
中,![]() ,
,
故二面角![]() 的大小为
的大小为![]() 。……………12分
。……………12分
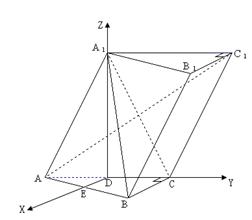
解法2:(I)如图,取![]() 的中点
的中点![]() ,则
,则![]() ,因为
,因为![]() ,
,
 所以
所以![]() ,又
,又![]() 平面
平面![]() ,
,
以![]() 为
为![]() 轴建立空间坐标系,
轴建立空间坐标系,
则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,由
,由![]() ,知
,知![]() ,
,
又![]() ,从而
,从而![]() 平面
平面![]() ;……………4分
;……………4分
(II)由![]()
![]() ,得
,得![]() 。
。
设平面![]() 的法向量为
的法向量为![]() ,
,![]() ,
,![]() ,所以
,所以
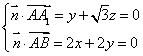 ,设
,设![]() ,则
,则![]()
所以点![]() 到平面
到平面![]() 的距离
的距离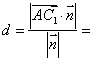
![]() 。……………8分
。……………8分
(III)再设平面![]() 的法向量为
的法向量为![]() ,
,![]() ,
,![]() ,
,
所以
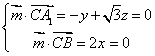 ,设
,设![]() ,则
,则![]() ,
,
故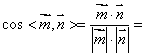
![]() ,根据法向量的方向,
,根据法向量的方向,
可知二面角![]() 的大小为
的大小为![]() 。……………12分
。……………12分
20.(13分)
解:(I)由已知得![]() , ………………………………2分
, ………………………………2分
![]() ,
,
![]() ,
,
上述两式错位相减得:![]() , ………………………………………5分
, ………………………………………5分
![]() ……………………………………………………6分
……………………………………………………6分
(II)![]() ,
,
∴当且仅当t = 0时,数列![]() 成等差数列,此时
成等差数列,此时![]() …………9分
…………9分
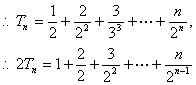
错位相减得:![]() ……………………………………………………10分
……………………………………………………10分
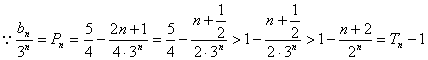 ,
,
![]() ……………………………………………………………… 12分
……………………………………………………………… 12分
21.(12分)
(1)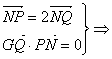 Q为PN的中点且GQ⊥PN
Q为PN的中点且GQ⊥PN
![]() GQ为PN的中垂线
GQ为PN的中垂线![]() PG=GN
PG=GN
∴GN+GM=MP=6,故G点的轨迹是以M、N为焦点的椭圆,其长半轴长![]() ,半焦距
,半焦距![]() ,∴短半轴长b=2,∴点G的轨迹方程是
,∴短半轴长b=2,∴点G的轨迹方程是![]() ………5分
………5分
(2)因为![]() ,所以四边形OASB为平行四边形
,所以四边形OASB为平行四边形
若存在l使得![]() =
=![]() ,则四边形OASB为矩形
,则四边形OASB为矩形![]()
若l的斜率不存在,直线l的方程为x=2,由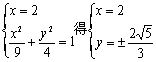
![]() 矛盾,故l的斜率存在. ………7分
矛盾,故l的斜率存在. ………7分
设l的方程为![]()
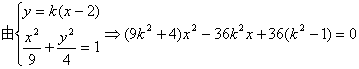
![]() ①
①
![]()
![]() ② ……………9分
② ……………9分
把①、②代入![]()
∴存在直线![]() 使得四边形OASB的对角线相等. ……………12分
使得四边形OASB的对角线相等. ……………12分
22.(14分)
解:(I)![]() ,
,
令![]() (舍去)
(舍去)
![]() 单调递增;
单调递增;
当![]() 单调递减. ……………………………………3分
单调递减. ……………………………………3分
![]() 上的极大值 ……………………………5分
上的极大值 ……………………………5分
(II)由![]() 得
得
![]() , …………① ……………………7分
, …………① ……………………7分
设![]() ,
,
![]() ,
,
依题意知![]() 上恒成立,
上恒成立,
![]() ,
,
![]() ,
,
![]() 上单增,要使不等式①成立,
上单增,要使不等式①成立,
当且仅当![]() ………………………9分
………………………9分
(III)由![]()
令![]() ,
,
当![]() 上递增;
上递增;
当![]() 上递减 ……………………11分
上递减 ……………………11分
而![]() ,
,
![]() 恰有两个不同实根等价于
恰有两个不同实根等价于
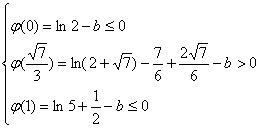
![]() ……………………………………14分
……………………………………14分
欢迎访问 http://www.k12zy.com
