珠海市2006-2007学年度第一学期期末中学教学质量调研监测
高三数学(文科)试题
2007.1
本试卷分选择题和非选择题两部分,共4页。 满分150分。考试用时120分钟。
参考公式:
圆锥表面积公式:![]() (r为底面半径,l为母线长)
(r为底面半径,l为母线长)
三棱锥体积公式:![]() (S为底面面积,h为高)
(S为底面面积,h为高)
导数公式:![]() ,
,![]()
第一部分 选择题(共50分)
一、选择题:本大题10个小题,每题5分,共50分。在每小题给出的四个选项中,只有一个是符合题目要求的。
1.![]() 是
是![]() 的
的
(A)充分但不必要条件 (B)必要但不充分条件
(C)充要条件 (D)既不充分也不必要条件
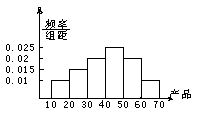 2. 一容量为20的样本,其频率分布直方图如右,
2. 一容量为20的样本,其频率分布直方图如右,
则样本在![]() 上的概率为
上的概率为
(A)0.75 (B)0.65
(C)0.8 (D)0.9
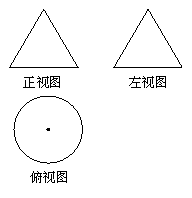 3. 如右图,一个空间几何体正视图与左视图为全等的
3. 如右图,一个空间几何体正视图与左视图为全等的
等边三角形,俯视图为一个半径为1的圆及其圆心,
那么这个几何体的全面积为
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
4.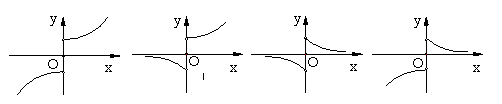 函数
函数![]() 的图象的大致形状是
的图象的大致形状是
(A) (B) (C) (D)
5. 在下面的程序框图中,输出的数![]()
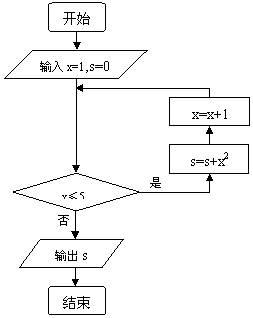 (A)25
(A)25
(B)30
(C)55
(D)91
6. 点![]() 和点
和点![]() 在直线
在直线![]() 两侧,则
两侧,则![]() 的范围是
的范围是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
7. ![]() 的最小正周期和最小值为
的最小正周期和最小值为
(A)![]() ,0
(B)2
,0
(B)2![]() ,0
,0
(C)![]() ,
,![]() (D)2
(D)2![]() ,
,![]()
8.直线![]() 与圆
与圆![]() 交于
交于![]() 二点,则
二点,则![]() 的面积为
的面积为
(A)3
(B)![]() (C)
(C)![]() (D)
(D)![]()
9.![]() ,若
,若![]() ,则
,则![]() 夹角为
夹角为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
10.对任意实数![]() ,定义运算
,定义运算![]() 为:
为:![]() ,则
,则![]() 的值域是( )
的值域是( )
(A)![]()
![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
第二部分 非选择题(共100分)
二、填空题:本大题共5个小题,其中第11-13题为必做题,每题5分,共15分;第14-15题为选做题,从中选做1题,每题5分,共5分。
11.![]() 在
在![]() 处的导数值是___________.
处的导数值是___________.
12.已知f (x)是定义在实数集R上的函数,且满足![]() ,
,![]() ,
,
则f (2007)=___________.
13.已知等式![]() ,
,![]() ,……,请你
,……,请你
写出一个具有一般性的等式,使你写出的等式包含了已知等式(不要求证明),那么这个
等式是:____________________________________________.
选做题:从以下2个小题中选做1题(只能做其中1题,做2个的,按得分最低的一道记分).
14.(几何证明选讲选做题)从不在⊙O上的一点A作直线交⊙O于B、C两点,且AB·AC=60,
OA=8,则⊙O的半径等于____________.
15.(坐标系与参数方程选做题)点P(-3,0)到曲线 上的点的最短
上的点的最短
距离为__________.
三、解答题:本大题共6个小题,共80分.解答应写出文字说明、演算步聚或推证过程.
16.(本小题满分12分)一个口袋中装有大小相同的2个白球和3个黑球.(1)若从口袋中随机地摸出一个球,求恰好是白球的概率;(2)若从口袋中一次随机地摸出两个球,求恰好都是白球的概率.
17.(本小题满分12分)在![]() 中,三边长分别为
中,三边长分别为![]() .
.
(1)求![]() 的值;
的值;
(2)求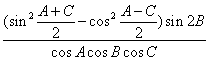 的值.
的值.
 18.(本小题满分14分) 如图,在棱长为2的正方体
18.(本小题满分14分) 如图,在棱长为2的正方体![]() 中,
中,
![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.
(1)求证:![]() //平面
//平面![]() ;
;
(2)求证:![]() ;
;
(3)求三棱锥![]() 的体积.
的体积.
19.(本小题满分14分)已知函数![]() 的图象关于原点对称,且当
的图象关于原点对称,且当![]() 时,
时,![]() .
.
(1)求a,b,c的值;
(2)当![]() 时,图象上是否存在两点,使得在这两点处的切线互相垂直?证明你的结论.
时,图象上是否存在两点,使得在这两点处的切线互相垂直?证明你的结论.
20.(本小题满分14分)已知中心在原点、焦点在![]() 轴上的椭圆的离心率是
轴上的椭圆的离心率是![]() ,椭圆上任意一点到两个焦点距离之和为4.(1)求椭圆标准方程;(2)设椭圆长轴的左端点为
,椭圆上任意一点到两个焦点距离之和为4.(1)求椭圆标准方程;(2)设椭圆长轴的左端点为![]() ,
,![]() 是椭圆上且位于第一象限的任意一点,
是椭圆上且位于第一象限的任意一点,![]() ,点B在椭圆上,R为直线AB与y轴的交点,证明:
,点B在椭圆上,R为直线AB与y轴的交点,证明:![]() .
.
21.(本小题满分14分)已知数列![]() 的每一项都是正数,满足
的每一项都是正数,满足![]() 且
且![]() ;等差数列
;等差数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)比较![]() 与2的大小;
与2的大小;
(3)若![]() 恒成立,求整数
恒成立,求整数![]() 的最小值.
的最小值.
珠海市2006-2007学年度第一学期期末中学教学质量调研监测
高三数学(文科)参考答案及评分标准
第一部分 选择题(共50分)
二、选择题:本大题10个小题,每题5分,共50分。在每小题给出的四个选项中,只有一个是符合题目要求的。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | B | B | B | C | B | C | D | D | B |
第二部分 非选择题(共100分)
二、填空题:本大题共5个小题,其中第11-13题为必做题,每题5分,共15分;第14-15题为选做题,从中选做1题,每题5分,共5分。
11.![]() 12.8 13.
12.8 13.![]() (n换成其它字母也对)
(n换成其它字母也对)
选做题:从以下两个小题中选做一题(只能做其中一题,做两个的,按得分最低的一道记分).
14.(几何证明选讲选做题)2或![]()
15.(坐标系与参数方程选做题)3
三、解答题:本大题共6个小题,共80分.解答应写出文字说明、演算步聚或推证过程.
16.(本小题满分12分)一个口袋中装有大小相同的2个白球和3个黑球.(1)若从口袋中随机地摸出一个球,求恰好是白球的概率;(2)若从口袋中一次随机地摸出两个球,求恰好都是白球的概率.
解:(1)用a、b、c、d、e分别表示五个球,其中a、b表示两个白球,c、d、e表示三个黑球.现从口袋中随机地摸出一个球,其基本事件有以下五种:
{a},{b},{c},{d},{e};…(2分)
设恰好是白球的事件为A,其中A包括两个基本事件:{a},{b}.…(4分)
A事件的概率P(A)=![]() .…(5分)
.…(5分)
答:若从口袋中随机地摸出一个球,恰好是白球的概率为![]() .…(6分)
.…(6分)
(2)若从口袋中一次随机地摸出两个球,其基本事件有以下十种:
{a,b},{a,c},{a,d},{a,e},{b,c},{b,d},{b,d},{c,d},{c,e},{d,e};
…(8分)
设恰好都是白球的事件为B,它包括的基本事件有一个:{a,b}.…(10分)
B事件的概率P(B)=![]() .…(11分)
.…(11分)
答:若从口袋中一次随机地摸出两个球,恰好都是白球的概率为![]() .…(12分)
.…(12分)
17.(本小题满分12分)在![]() 中,三边长分别为
中,三边长分别为![]() .
.
(1)求![]() 的值;
的值;
(2)求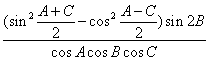 的值.
的值.
解:(1)![]() …(1分)
…(1分)
![]() …(3分)
…(3分)
![]() …(5分)
…(5分)
(2).![]() 为三角形内角,
为三角形内角,![]()
![]() …(6分)
…(6分)
![]() 原式
原式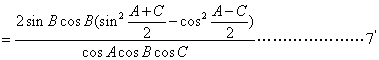
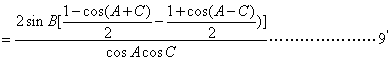
=![]() …(10分)
…(10分)
![]()
![]() …(11分)
…(11分)
![]() …(12分)
…(12分)
 18.(本小题满分14分) 如图,在棱长为2的正方体
18.(本小题满分14分) 如图,在棱长为2的正方体![]() 中,
中,
![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.
(1)求证:![]() //平面
//平面![]() ;
;
(2)求证:![]() ;
;
(3)求三棱锥![]() 的体积.
的体积.
解:
(1)连接![]() ,已知
,已知![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.
EF是三角形BD1D的中位线,\EF//BD1;…(3分)
又![]() ,
,![]() ,\EF//面BD1C1…(5分)
,\EF//面BD1C1…(5分)
(2)连接![]() 、BC1,
、BC1,
正方体中,D1C1^面BCC1B1,BC1Ì面BCC1B1,所以D1C1^ B1C…(6分)
在正方形BCCB中,两对角线互相垂直,即BC1^B1C,…(7分)
D1C1 、BC1Ì面BC1D1,所以B1C^面BC1D1…(8分)
BD1Ì面BC1D1,所以有B1C^ BD1,…(9分)
在(1)已证:EF//BD1,所以EF^B1C.…(10分)
(3)连接B1D1,在各直角三角形中,计算得:
EB1=3,EF=![]() ,FB1=
,FB1=![]() ,FC=
,FC=![]() ,B1C=
,B1C=![]() , …(12分)
, …(12分)
![]() …(14分)
…(14分)
19. (本小题满分14分)已知函数![]() 的图象关于原点对称,且当
的图象关于原点对称,且当![]() 时,
时,![]() .
.
(1)求a,b,c的值;
(2)当![]() 时,图象上是否存在两点,使得在这两点处的切线互相垂直?证明你的结论.
时,图象上是否存在两点,使得在这两点处的切线互相垂直?证明你的结论.
解:(1)依题意,对任意实数x都有:![]() ,
,
可得:![]() ,b=0;…(2分)
,b=0;…(2分) ![]() …(3分)
…(3分)
又当![]() 时,
时,![]() ,
,
所以:![]() ,
,![]() .…(5分)
.…(5分)
解得:![]() ,故
,故 ![]() .…(6分)
.…(6分)
(2)当![]() 时,图象上不存在两点,使得在这两点处的切线互相垂直.
时,图象上不存在两点,使得在这两点处的切线互相垂直.
假设当![]() 时,图象存在两点
时,图象存在两点![]() ,使得在这两点处的切线互相垂直.设这两条切线的斜率分别为
,使得在这两点处的切线互相垂直.设这两条切线的斜率分别为![]() 和
和![]() ,则有
,则有![]() .…(8分)
.…(8分)
则由![]() 知这两点处的切线的斜率分别为:
知这两点处的切线的斜率分别为:![]() ,且
,且
![]() …(10分)
…(10分)
![]()
![]()
这与(*)相矛盾,故假设不成立.…(13分)
所以当![]() 时,图象上不存在两点,使得在这两点处的切线互相垂直.…(14分)
时,图象上不存在两点,使得在这两点处的切线互相垂直.…(14分)
20.(本小题满分14分)已知中心在原点、焦点在![]() 轴上的椭圆的离心率是
轴上的椭圆的离心率是![]() ,椭圆上任意一点到两个焦点距离之和为4.(1)求椭圆标准方程;(2)设椭圆长轴的左端点为
,椭圆上任意一点到两个焦点距离之和为4.(1)求椭圆标准方程;(2)设椭圆长轴的左端点为![]() ,
,![]() 是
是
椭圆上且位于第一象限的任意一点,![]() ,点B在椭圆上,R为直线AB与y轴的交点,证明:
,点B在椭圆上,R为直线AB与y轴的交点,证明:![]() .
.
解:(1)根据题设,可设椭圆标准方程为:![]() …(1分)
…(1分)
则离心率![]() ,由椭圆定义,得
,由椭圆定义,得![]() …(2分)
…(2分)
解得![]() ,
,![]() …(3分)
…(3分)
所以椭圆标准方程为:![]() …(4分)
…(4分)
(2)由题意得![]() ,设
,设![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,
点P和点B都在椭圆上,则有![]() , (1)
, (1)
![]() (2) …(5分)
(2) …(5分)
由![]() ,有
,有![]() ,即
,即![]() , (3)…(6分)
, (3)…(6分)
由![]() 可知
可知![]() .
.
AB直线方程为:![]()
把![]() 代入,得
代入,得![]() …(7分)
…(7分)
所以有![]() ,
,![]() ,
,![]() ,
,
可得:![]() (4)…(8分)
(4)…(8分)
![]()
![]() (5)…(9分)
(5)…(9分)
由(1),(2),(3)得:![]() (6)…(10分)
(6)…(10分)
由(1),(5)得:![]() (7)…(11分)
(7)…(11分)
由(2),(4)得:![]() (8)…(12分)
(8)…(12分)
由(7),(6)得:![]() (9)…(13分)
(9)…(13分)
由(8),(9)可证得:![]() .…(14分)
.…(14分)
21.(本小题满分14分)已知数列![]() 的每一项都是正数,满足
的每一项都是正数,满足![]() 且
且![]() ;等差数列
;等差数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)比较![]() 与2的大小;
与2的大小;
(3)若![]() 恒成立,求整数
恒成立,求整数![]() 的最小值.
的最小值.
(1)由![]() 有,
有,![]() ,…(2分)
,…(2分)
由于数列![]() 的每一项都是正数,
的每一项都是正数,![]() …(3分)
…(3分)
设![]() ,由已知有
,由已知有![]() ,…(4分)
,…(4分)
解得![]()
![]() …(5分)
…(5分)
(2)当![]() 时,
时,![]() …(6分)
…(6分)
当![]() 时,
时,![]() …(8分)
…(8分)
![]()
![]() …(10分)
…(10分)
(3)记![]()
![]() …(11分)
…(11分)
所以 ![]()
两式相减得 ![]() …(12分)
…(12分)
![]() 递增,
递增,![]() 最小的整数
最小的整数![]() …(14分)
…(14分)