1平行关系
例题讲解：
例1：已知四面体ABCD中，M、N分别是△ABC和△ACD的重心，求证：
(1)MN∥平面ABD；
(2)BD∥平面CMN。
答案与提示：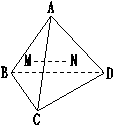
连CM、CN分别交AB、AD于E、F，连EF，易证
MN∥EF∥BD
例2.已知边长为10的等边三角形ABC的顶点A在平面α内，顶点B、C在平面α的上方，BD为AC边上的中线，B、C到平面α的距离BB1=2，CC1=4．
(1)求证：BB1∥平面ACC1
(2)求证：BD⊥平面ACC1
(3)求四棱锥A-BCC1B1的体积
答案与提示：（3）30
例3.已知PA⊥平面ABCD，四边形ABCD是矩形，M、N分别是AB、PC的中点.
(1) 求证：MN∥平面PAD；
(2) 求证：MN⊥CD；
(3)
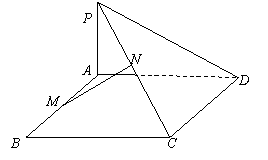若平面PCD与平面ABCD所成二面角为θ，问能否确定θ的值，使得MN是异面直线AB与PC的公垂线.
答案与提示：（3）45°
备用题
如图,在三棱锥P-ABC中，PA⊥面ABC，△ABC为正三角形， D、E分别为BC、AC的中点，设AB=2PA=2，
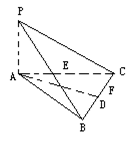(1)如何在BC上找一点F，使AD∥平面PEF？说明理由；
(2)对于(1)中的点F，求二面角P-EF-A的大小；
答案与提示：（1）F为CD中点（2）arctan2
作业
在正四棱柱ABCD-A1B1C1D1中，AA1=AB，点E、M分别为A1B、C1C的中点，过A1，B，M三点的平面交C1D1于点N。
(1)求证：EM∥平面ABCD；
(2)求二面角B-A1N-B1的正切值。
答案与提示：（2）arctan
2垂直关系
例题讲解：
例1：如图,在三棱锥P-ABC中，AB=BC=CA，PA⊥底面ABC，D为AB的中点．
(1)求证：CD⊥PB；
(2)设二面角A-PB-C的平面角为α，且tanα=，若底面边长为1，求三棱锥P-ABC的体积．
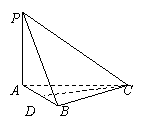答案与提示：（2）
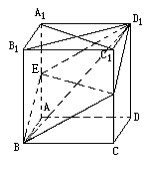例2：已知ABCD—A1B1C1D1是棱长为a的正方体，E、F分别是棱AA1和CC1的中点，G是A1C1的中点．
(1)求证平面BFD1E⊥平面BGD1；
(2)求点G到平面BFD1E的距离；
(3)求四棱锥A1-BFD1E的体积．
答案与提示：（2）a (3) a3
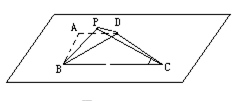
例3：四边形ABCD中．AD∥BC，AD=AB，∠BCD=45°，∠BAD=90°，将△ABD沿对角线BD折起，记折起点A的位置为P，且使平面PBD⊥平面BCD．
(1)求证：CD⊥平面PBD；
(2)求证：平面PBC⊥平面PDC；
(3)求二面角P—BC—D的大小．
答案与提示：(2)先证PB⊥面PCD (3)arctan
备用题
在三棱锥S-ABC中，已知SA=4，AB=AC，BC=3,∠SAB=∠SAC=45°,SA与底面ABC所的角为30°.
(1)求证：SA⊥BC；
|
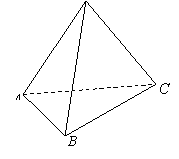(3)求三棱锥S—ABC的体积．
答案与提示：(2)arctan(3)9
作业
1.在四棱锥P-ABCD中，已知PD⊥底面ABCD，底面ABCD为等腰梯形,且∠DAB=60°，AB=2CD，∠DCP=45°，设CD=a．
(1)求四棱锥P-ABCD的体积．
(2)求证：AD⊥PB．
答案与提示：(1) a3
2.如图，正三角形ABC与直角三角形BCD成直二面角，且∠BCD=90°，∠CBD=30°.
（1）求证：AB⊥CD；
（2）求二面角D—AB—C的大小；
答案与提示：(2)arctan
3 空间角
例1、如图1，设ABC-A
BC是直三棱柱，F是AB的中点，且
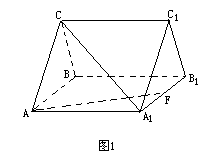
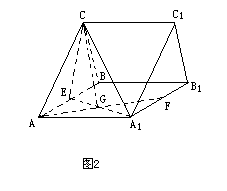
(1)求证：AF⊥AC； (2)求二面角C-AF-B的大小．
解：(1)如图2，设E是AB的中点，连接CE，EA．由ABC-ABC是直三棱柱，知AA⊥平面ABC，而CE平面ABC，所以CE⊥AA，
∵AB=2AA=2a，∴AA=a，AA⊥AE，知AAFE是正方形，从而AF⊥AE．而AE是AC在平面AAFE上的射影，故AF⊥AC；
(2)设G是AB与A1E的中点，连接CG．因为CE⊥平面AABB，AF⊥AE，由三垂线定理，CG⊥AF，所以∠CGE就是二面角C-AF-B的平面角．∵AAFE是正方形，AA=a，
∴
，
∴
，
∴tan∠CGE=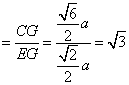
，∠CGE＝
，从而二面角C-AF-B的大小为。
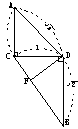
例2、 一条长为2的线段夹在互相垂直的两个平面a、b之间，AB与a成45o角，与b成
角，过A、B两点分别作两平面交线的垂线AC、BD，求平面ABD与平面ABC所成的二面角的大小．
 | |||
 | |||
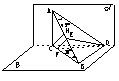以CD为轴，将平 以AB为轴，将平
 |  |
面BCD旋转至与
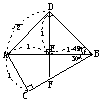面ABD旋转至与
平面ACD共面 平面ABC共面
图 1 图 2 图 3
解法１、过D点作DE⊥AB于E，过E作EF⊥AB交BC于F(图1)，连结DF，则∠DEF即为二面角D－AB－C的平面角．
为计算△DEF各边的长，我们不妨画出两个有关的移出图．在图2中，可计算得DE＝1，EF＝
，BF＝
＝
．在移出图3中，
∵ cosB＝
＝
,
在△BDF中，由余弦定理：
DF 2＝BD 2＋BF 2－2BD ﹒ BF ﹒ cosB
＝(
)2＋()2 －2﹒﹒ ＝
．
（注：其实，由于AB⊥DE，AB⊥EF，∴ AB⊥平面DEF，∴ AB⊥DF．
又∵ AC⊥平面b， ∴ AC⊥DF． ∴ DF⊥平面ABC， ∴ DF⊥BC，即DF是Rt△BDC斜边BC上的高，于是由BC ﹒ DF＝CD ﹒BD可直接求得DF的长．）
在△DEF中，由余弦定理：
cos∠DEF＝
＝
＝
.
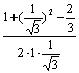∴ ∠DEF＝arccos.此即平面ABD与平面ABC所成的二面角的大小．
解法２、过D点作DE⊥AB于E，过C作CH⊥AB于H，则HE是二异面直线CH和DE的公垂线段，CD即二异面直线上两点C、D间的距离．运用异面直线上两点间的距离公式，得：
CD 2＝DE 2＋CH 2＋EH 2－2DE CH cosq (*)
（注：这里的q是平面ABD与平面ABC所成的二面角的大小，当0＜q o≤90o，q 亦即异面直线CH与DE所成的角；当90o＜q ＜180o，异面直线所成的角为180o－q .）
∵ CD＝DE＝1，CH＝
，HE＝
，
从而算得 cosq＝， ∴ q＝arccos.
例3、如图1，直三棱柱ABC－ABC的各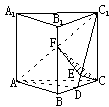
条棱长都相等，
D为棱BC上的一点，在截面ADC中，若∠ADC＝
，
求二面角D－AC1－C的大小．
解：由已知，直三棱柱的侧面均为正方形， 图 7
∵ ∠ADC1＝90o，即AD⊥C1D．又CC1⊥平面ABC，
∴ AD⊥CC1. ∴ AD⊥侧面BC1，∴ AD⊥BC， 图1
∴ D为BC的中点．
过C作CE⊥C1D于E，∵ 平面ADC1⊥侧面BC1，
∴ CE⊥平面ADC1．取AC1的中点F，连结CF，则CF⊥AC1．
连结EF，则EF⊥AC1(三垂线定理)
∴ ∠EFC是二面角D－AC1－C的平面角．
在Rt△EFC中，sin∠EFC＝
. ∵ BC＝CC1＝a
易求得 CE＝
，CF＝
.
∴ sin∠EFC＝
， ∴ ∠EFC＝arcsin.
∴ 二面角D－AC1－C的大小为arcsin.
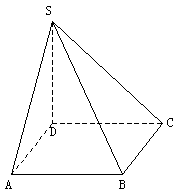
例4、（2004年北京春季高考题）如图，
四棱锥
的底面是边长为1的正方形，
图（1）
SD垂直于底面ABCD，SB=√3。
（I）求证
；
（II）求面ASD与面BSC所成二面角的大小；
（III）设棱SA的中点为M，求异面直线DM与SB所成角的大小。
(Ⅳ)求SD与面SAB所成角的大小。
分析：本小题主要考查直线与平面的位置关系等基本知识，考查空间想象能力、逻辑思维能力和运算能力。
（I）证明：如图1
∵底面ABCD是正方形 
SD⊥底面ABCD 
DC是SC在平面ABCD上的射影
由三垂线定理得
（II）解：SD⊥底面ABCD，且ABCD为正方形
可以把四棱锥补形为长方体
，如图2
面ASD与面BSC所成的二面角就是面
与面
所成的二面角，
又
为所求二面角的平面角
在
中，由勾股定理得
在
中，由勾股定理得
即面ASD与面BSC所成的二面角为
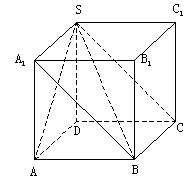
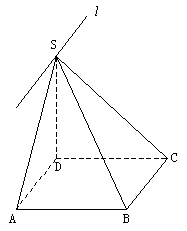
图2 图3
（III）解：如图3 
是等腰直角三角形 又M是斜边SA的中点
面ASD，SA是SB在面ASD上的射影
由三垂线定理得
异面直线DM与SB所成的角为
(Ⅳ) 45°
练习：1.设△ABC和△DBC所在的两个平面互相垂直，且AB=BC=BD，∠ABC=
∠DBC=120º.求：
(1).直线AD与平面BCD所成角的大小.
(2).异面直线AD与BC所成的角.
(3) .二面角A-BD-C的大小.
答案：（1）45°（2）90°（3）180°-arctan2
2..如图，正三棱柱ABC-A1B1C1的底面边长为2，侧棱长为，D,E分别为AA1,B1C1的中点.
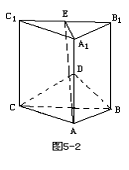(1)求证：平面AA1E⊥平面BCD；
(2)求直线A1B1与平面BCD所成的角．
答案：（2）30°
3.如图,四棱锥P-ABCD中，底面ABCD是边长为a的正方形，PD=a，PA=PC=a，
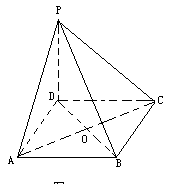(1)求证：PD⊥平面ABCD；
(2)求异面直线PB与AC所成角的大小；
(3)求二面角A-PB-D的大小；
(4)在这个四棱锥中放入一个球，求球的最大半径．
答案：（2）90°（3）60°(4)(2-√2)a/2
4.在三棱锥S-ABC中，已知SA=4，AB=AC，BC=3,∠SAB=∠SAC=45º,SA与底面ABC所成的角为30º.
(1)求证：SA⊥BC；
(2)求二面角S—BC—A的大小;
(3)求三棱锥S—ABC的体积．
答案：（3）9
4 距离
|
角三角形，∠ACB=900，AC=1，C点到AB1的距离为
CE=
，D为AB的中点.
（1）求证：AB1⊥平面CED；
（2）求异面直线AB1与CD之间的距离；
（3）求二面角B1—AC—B的平面角.
解:（1）∵D是AB中点，△ABC为等腰直角三角形，
∠ABC=900，∴CD⊥AB又AA1⊥平面ABC，∴CD⊥AA1.
∴CD⊥平面A1B1BA ∴CD⊥AB1，又CE⊥AB1，
∴AB1⊥平面CDE；
（2）由CD⊥平面A1B1BA ∴CD⊥DE
∵AB1⊥平面CDE ∴DE⊥AB1,
∴DE是异面直线AB1与CD的公垂线段
∵CE=，AC=1 , ∴CD=
∴
；
（3）连结B1C，易证B1C⊥AC，又BC⊥AC ,
∴∠B1CB是二面角B1—AC—B的平面角.
在Rt△CEA中，CE=，BC=AC=1,∴∠B1AC=600
∴
， ∴
,
∴ 
, ∴
.
例2、如图，正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直。点M在AC上移动，点N在BF上移动，若CM=BN=
（1） 求MN的长；
（2） 当为何值时，MN的长最小；
（3） 当MN长最小时，求面MNA与面MNB所成的二面角
的大小。
例3. 如图，平面a∩平面b＝MN，
二面角A－MN－B为60°,点A∈a，
B∈b，C∈MN，∠ACM＝∠BCN＝45°.
AC＝1,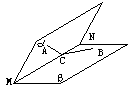 
(1) 求点A到平面b的距离；
(2) 求二面角A－BC－M的大小．
答案(1)
； (2)arctan
(提示：求出点A在平面 b 的射影到直线BC的距离为
).
例4、已知直三棱柱ABC－A1B1C1的侧棱AA1＝4cm，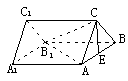
它的底面△ABC中有AC＝BC＝2cm，∠C＝90°,E是AB的
中点．
(1) 求证：CE和AB1所在的异面直线的距离等于
cm；
(2) 求截面ACB1与侧面ABB1A1所成的二面角的大小．
答案 (2) arccos.
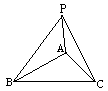
练习：1.已知：如图，△ABC中，AB=6cm，AC=8cm，BC=10cm，P是平面ABC外一点，且PA=PB=PC=6cm．
(1)求点P到平面ABC的距离；
(2)求PA与平面ABC所成角的余弦．
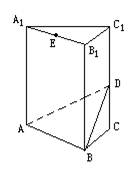2.如图，正三棱柱A1B1C1-ABC中，底面边长和侧棱长都是1，D、E分别是C1C和A1B1的中点．
(1)求点E到平面ABD的距离：
(2)求二面角A—BD—C的正切值．
3.如图，正三棱柱ABC-A1B1C1的九条棱均相等，D是BC上一点，AD⊥C1D.
(1).求证：截面ABC1⊥侧面BCC1B1.
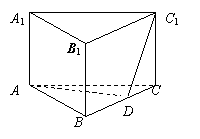(2)求二面角C-AC1-D的大小.
(3)若AB=2，求直线A1B与截面ADC1的距离.
.
4.在棱长为a的正方体ABCD-A1B1C1D1中，E、F分别是BC、A1D1的中点.
(1)求证：四边形B1EDF是菱形；
(2)求直线A1C与DB的距离；
(3)求直线AD与平面B1EDF所成的角.
(4)求平面B1D1C与A1DB的距离
5多 面 体
例1．斜三棱柱ABC—A1B1C1的底面是边长为a的正三角形，侧棱长为b，
侧棱AA1和AB、AC都成45°的角，求棱柱的侧面积和体积.
例2．三棱锥各侧面与底面均成45°角，底面三角形三内角A、B、C满足2B＝A＋C，最大边与最小边是方程3x2－27x＋32=0的两根．
（1）求棱锥的高；（2） 求棱锥的侧面积．
例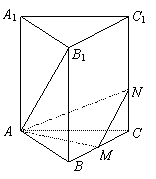
3．如图，正三棱柱ABC-A1B1C1的所有棱长都为4，M是BC的中点，N是CC1上一点，满足MN⊥AB1
（1）试求三棱锥
的体积；
（2）求点C1到平面AMN的距离。
 |
例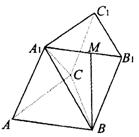
4．如图，三棱柱
的底面是边长为a的正三角形，侧面
是菱形且垂直于底面，∠
＝60°，M是
的中点．
（1）求证：BM⊥AC；
（2）求二面角
的正切值；
（3）求三棱锥
的体积．
习题
1．正三棱锥P－ABC的底面边长为a，E、F分别是侧棱PB、PC的中点，且E、A、F三点的截面垂直于侧面PBC．
（1） 求棱锥的全面积；（2） 侧面与底面所成的角的余弦值．
2．如图，直四棱柱
的侧棱
的长是a，底面ABCD是边长AB=2a，BD=a的矩形，E为
的中点。
(.1)求二面角E-BD-C的大小;
(2)求三棱锥
的体积.
3．如图，正三棱柱的底面边长为a，点M在边BC上，△
是以点M为直角顶点的等腰直角三角形．
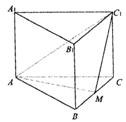
（1）求证点M为边BC的中点；
（2）求点C到平面的距离；
（3）求二面角
的大小．
答案：
例题
1． 
，
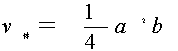
2．作PO
面ABC，作OD,OE,OF分别垂直于三边，连结PD，PE，PF，，易得，B＝600
,
=7,
,
,
3．三棱锥的体积为
， 点C1到平面AMN的距离为
4．（1）证明：∵ 是菱形，∠＝60°
△
是正三角形
又∵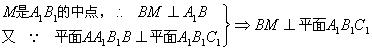 
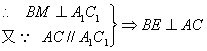
（2）
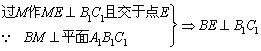∴ ∠BEM为所求二面角的平面角
△
中，
60°
，Rt△
中，
60°
∴ 
， ∴ 所求二面角的正切值是2；
（3）
习题
1．
，
2. 二面角E-BD-C的大小为45°，三棱锥的体积为
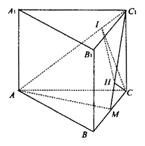3．（1）∵ △为以点M为直角顶点的等腰直角三角形，∴ 
且
．∵ 正三棱柱， ∴ 
底面ABC．
∴ 
在底面内的射影为CM，AM⊥CM．
∵ 底面ABC为边长为a的正三角形，∴ 点M为BC边的中点．
（2）过点C作CH⊥
，由（1）知AM⊥且AM⊥CM，
∴ AM⊥平面
∵ CH在平面内， ∴ CH⊥AM，
∴ CH⊥平面
，由（1）知，
，
且
．
∴ 
． ∴ 
．
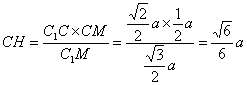∴ 点C到平面的距离为底面边长为
．
（3）过点C作CI⊥
于I，连HI， ∵ CH⊥平面，
∴ HI为CI在平面内的射影，
∴ HI⊥，∠CIH是二面角的平面角．
在直角三角形
中，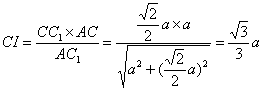
，
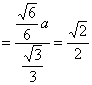， ∴ ∠CIH＝45°， ∴ 二面角的大小为45°
6球
例1．设地球是半径为R的球，地球上A、B两地都在北纬45°上，A、B两点的球面距离是pR，A在东经20°，求点B的位置
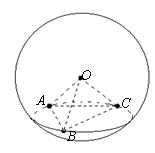
例2．半径为13cm的球面上有A、B、C三点，每两点间的距离是AB=6cm，BC=8cm，CA=10cm，求这三点所在的平面到球心的距离.
例3．半球内有一内接正方体，正方体的一个面在半球的底面圆内，若正方体的一边长为
，求半球的表面积和体积。
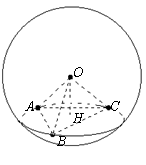
例4．如图，A、B、C是半径为1的球面上的三点，B、C两点间的球面距离为
π，点A与B、C两点间的球面距离均为
，O为球心，求：
（1）∠BOC、∠AOB的大小；
（2）球心O到截面ABC的距离.
习题
1．已知正方体的全面积为24，求：（1）求外接球的表面积； （2）求内切球的表面积.
2．一个正四面体的棱长为2，求该四面体的外接球的体积.
3．在120°的二面角内放一个半径为5的球，分别切两个半平面于点A、B，求这两个切点A、B在球面上的最短距离
答案：
例题
1．东径1100，或者西径70° 2．12cm
3. 18π，， 18π
4. ∠BOC=
, ∠AOB=
, 球心O到截面ABC的距离为
习题
1．外接球的表面积为12π，内切球的表面积为4π， 2．36π
3．
7综合应用(1)
例题讲解：
例1：如图，在斜四棱柱ABCD—A1B1C1D1中，底面ABCD是边长为4的菱形，∠DAB＝60°，若点A1在平面ABCD上的射影是BD的中点，设点E是CC1上的中点，AA1＝4．
(1)求证：BB1D1D是矩形；
(2)求二面角E—BD—C的大小；
(3)求四面体B1—BDE的体积．
答案与提示：(2)arccos (3)
例2：三棱锥S—ABC中，底面△ABC是顶角为∠ABC=α、AC=a的等腰三角形，SCA=，SC=b，侧面SAC与底面ABC所成二面角为θ（0<θ≤）,E、D分别为SA和AC的中点.
（1）求证无论θ，α为何值时，点S到截面BDE的距离为定值;
（2）求三棱锥S—ABC的体积.
答案与提示：(1)(2) c2bcotsinθ
例3：如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB交PB于点F.
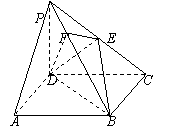(1)求证：PA∥平面EBD；
(2)求证：PB⊥平面EFD；
(3)求二面角C-PB-D的大小.
答案与提示：(3)60°
备用题：
1.如图，已知四棱锥S-ABCD的底面是边长为
的正方形，BD和AC相交于O点，侧面SAB是等边三角形，且平面SAB
平面ABCD。
(1)求SO与平面SAB所成的角；
(2)求二面角B－SA－C的大小；
(3)求点C到平面SBD的距离。
答案与提示：(1)30°(2)arctan
作业
1.已知矩形ABCD中，AB=1，BC=a(a>0)，PA⊥平面ABCD，且PA=1.
(1)问BC边上是否存在点Q，使得PQ⊥QD；
(2)若BC边上有且仅有一个点Q，使得PQ⊥QD ，求这时二面角Q-PD-A的大小.
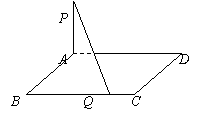答案与提示：(1)当a≥2时存在，当a<2时不存在 (2)arctan
2.如图，四棱锥P-ABCD中，PB⊥底面ABCD，CD⊥PD，底面ABCD为直角梯形，AD∥BC，AB⊥BC，AB=AD=PB=3，点E在棱PA上，且PE=2EA.
(1)
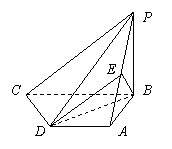求异面直线PA与CD所成的角；
(2) 求证：PC∥平面EBD；
(3) 求二面角A-BE-D的大小.
答案与提示：(1) 60° (3)arctan
8综合应用(2)
例题讲解：
例1：已知斜三棱柱ABC-A’B’C’的底面是直角三角形，∠C=90°，侧棱与底面所成的角为α
（0°<α<90°），B’在底面上的射影D落在BC上。
（1）求证：AC⊥面BB’C’C。
（2）当α为何值时，AB’⊥BC’，且使得D恰为BC的中点。
答案与提示：(2) 60°
例2：如图，已知
面
，
于D，
。
（1）令
，
，试把
表示为
的函数，并求其最大值；
（2）在直线PA上是否存在一点Q，使得
？
答案与提示：(1) = 最大值为 (2)存在
例3：长方体
中，
，
，
是侧棱
中点．
（1）求直线
与平面
所成角的大小；
（2）求二面角
的大小；
（3）求三棱锥
的体积．
答案与提示：(1)45°(2) 
(3)
备用题：
如图，直四棱柱中ABCD-A1B1C1D1，底面ABCD为直角梯形，AB∥CD，∠ABC=90°，AA1=2AB=4，E、F分别为AA1、DD1上的点，且A1E=DF=1=BC=CD.
(1)
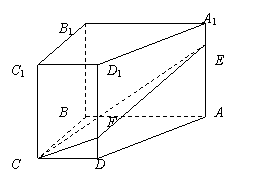求直线EF与平面ABB1A1所成的角；
(2) 求证：平面CEF⊥平面ADD1A1.
答案与提示：(1)arctan(2)证AF⊥面CEF
作业
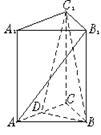1.如图，已知正三棱柱ABC—A1B1C1中，过BC1的平面BC1D∥AB1，平面BC1D交AC于D.
（1）求证BD⊥平面ACC1A1；
（2）若二面角C1—BD—C等于60°，求平面BC1D与平面BCC1B1所成二面角的大小.（结果用反三角函数表示）
答案与提示：(2)arctan
2.如图，已知四边形ABCD为直角梯形，AB∥CD，∠BAD=90°，PA⊥平面ABCD，CD=2，PA=AD=AB=1，E为PC的中点.
（1）求证：EB∥平面PAD；
（2）求直线BD与平面PCD所成的角；
（3）求二面角A—PC—D的大小.
答案与提示：(2)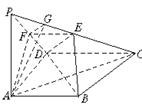
30°(3) arctan