嘉定区2007学年第一学期高三数学调研试卷
| 题 号 | 一 | 二 | 三 | 总 分 | |||||
| 1—11 | 12—15 | 16 | 17 | 18 | 19 | 20 | 21 | ||
| 得 分 | |||||||||
|
一.填空题(本大题满分44分)本大题共有11题,只要求直接
填写结果,每个空格填对得4分,否则一律得零分.
1.不等式![]() 的解集是_______________________.
的解集是_______________________.
2.计算:![]() ____________________.
____________________.
3.函数![]() 的最小正周期是__________________.
的最小正周期是__________________.
4.函数![]() (
(![]() )的反函数是
)的反函数是![]() _________________________.
_________________________.
5.若复数![]() (
(![]() 为虚数单位)是纯虚数,则实数
为虚数单位)是纯虚数,则实数![]() _________________.
_________________.
6.若![]() 是方程
是方程![]() 的解,其中
的解,其中![]() ,则
,则![]() ________________.
________________.
7.无穷数列![]() 中,
中,![]() ,则
,则![]() _______________.
_______________.
8.已知直线![]() 与圆
与圆![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() ,则
,则![]() _________________.
_________________.
9.某学习小组共有![]() 名同学,其中男生
名同学,其中男生![]() 名
名![]() ,现从中选出
,现从中选出![]() 人参加一项调查活
人参加一项调查活
动,若至少有一名女生参加的概率为![]() ,则
,则![]() = _____________.
= _____________.
10.函数![]() 的图像与
的图像与![]() 轴、定直线
轴、定直线![]() 及动直线
及动直线![]() (
(![]() )所围成图形(位
)所围成图形(位
于两条平行直线![]() 与
与![]() 之间的部分)的面积为
之间的部分)的面积为![]() ,则
,则![]() 关于
关于![]() 的函数关系式
的函数关系式
![]()
![]() ____________________.
____________________.
11.设集合![]() ,在
,在![]() 上定义关于
上定义关于![]() 的函数
的函数![]() ,
,
则集合![]() 用列举法可表示为________________.
用列举法可表示为________________.
|
代号为A、B、C、D的四个结论,其中有且只有一个结论
是正确的,必须把正确结论的代号写在题后的圆括号内,
选对得4分,不选、选错或者选出的代号超过一个(不论
是否都写在圆括号内),一律得零分.
12.在平面直角坐标系内,直线![]() 和直线
和直线![]() (
(![]() )的关系是…………………………………………………………………………………( )
)的关系是…………………………………………………………………………………( )
(A)互相平行 (B)互相垂直
(C)关于原点对称
(D)关于直线![]() 对称
对称
13.已知![]() ,则
,则![]() =………………( )
=………………( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
14.设函数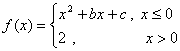 ,若
,若![]() ,
,![]() ,则关于
,则关于![]() 的
的
方程![]() 的解的个数是…………………………………………………………( )
的解的个数是…………………………………………………………( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
15.下列4个命题中,真命题是……………………………………………………………( )
(A)如果![]() ,那么
,那么![]() 的充要条件是
的充要条件是![]()
(B)如果![]() 为△
为△![]() 的两个内角,那么
的两个内角,那么![]() 的充要条件是
的充要条件是![]()
(C)如果向量![]() 与向量
与向量![]() 均为非零向量,那么
均为非零向量,那么![]()
(D)函数![]() 的最小值为
的最小值为![]()
三.解答题(本大题满分90分)本大题共有6题,解答下列各题必须写出必要的步骤.
 16.(本题满分12分)
16.(本题满分12分)
已知集合![]() ,(
,(![]() 为虚数单位),
为虚数单位),
集合![]() ,若
,若![]() ,求实数
,求实数![]() 的取值
的取值
范围.
![]() 17.(本题满分14分.本题共有2个小题,第(1)题满分6
17.(本题满分14分.本题共有2个小题,第(1)题满分6
分,第(2)题满分8分.)
已知向量![]() ,
,![]() ,函数
,函数![]() .
.
(1)求函数![]() 的最大值,并求当
的最大值,并求当![]() 取得最大值时
取得最大值时![]() 的集合;
的集合;
(2)当![]() 时,求函数
时,求函数![]() 的值域.
的值域.

![]() 18.(本题满分14分,第(1)题6分,第(2)题8分)
18.(本题满分14分,第(1)题6分,第(2)题8分)
统计数据表明,某种型号的大型卡车在匀速行驶中每小时耗油量![]() (升)关于行驶速度
(升)关于行驶速度![]() (千米/小时)的函数解析式可以表示为
(千米/小时)的函数解析式可以表示为![]() (
(![]() ).已知甲、乙两地相距
).已知甲、乙两地相距![]() 千米.
千米.
(1)当卡车以![]() 千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当卡车以多大的速度匀速行驶,从甲地到乙地耗油最少?最少耗油多少升?
|
19.(本题满分14分)本题共有2个小题,第(1)题满分4
分,第(2)题满分10分.
在平面直角坐标系![]() 中,
中,![]() 为坐标原点,以
为坐标原点,以![]() 为圆心的圆与直线
为圆心的圆与直线![]() 相切.
相切.
(1)求圆![]() 的方程;
的方程;
(2)设圆![]() 与
与![]() 轴的两个交点为
轴的两个交点为![]() 、
、![]() ,圆内的动点
,圆内的动点![]() 使
使![]() ,
,![]() ,
,![]() 成等比数列,求
成等比数列,求![]() 的取值范围.
的取值范围.
|
20.(本题满分18分)本题共有3个小题,第(1)题满分5
分,第(2)题满分6分,第(3)题满分7分.
数列![]() 满足
满足![]() ,
,![]() (
(![]() ),且
),且![]() 从第二项起是公差为
从第二项起是公差为![]() 的等差数列,
的等差数列,![]() 是
是![]() 的前
的前![]() 项和.
项和.
(1)当![]() 时,用
时,用![]() 与
与![]() 表示
表示![]() 与
与![]() ;
;
(2)若在![]() 与
与![]() 两项中至少有一项是
两项中至少有一项是![]() 的最小值,试求
的最小值,试求![]() 的取值范围;
的取值范围;
(3)若![]() 为正整数,在(2)的条件下,设
为正整数,在(2)的条件下,设![]() 取
取![]() 为最小值的概率是
为最小值的概率是![]() ,
,![]() 取
取![]() 为最小值的概率是
为最小值的概率是![]() ,比较
,比较![]() 与
与![]() 的大小.
的大小.
|
21.(本题满分18分)本题共有3个小题,第(1)题满分4
分,第(2)题满分6分,第(3)题满分8分.
已知函数![]() ,
,![]() 且
且![]() .
.
(1)求实数![]() 的值;
的值;
(2)判断函数![]() 在区间
在区间![]() 上的单调性,并用函数单调性的定义证明;
上的单调性,并用函数单调性的定义证明;
(3)求实数![]() 的取值范围,使得关于
的取值范围,使得关于![]() 的方程
的方程![]() 分别为:
分别为:
① 有且仅有一个实数解;② 有两个不同的实数解;③ 有三个不同的实数解.
嘉定区2007学年第一学期高三数学调研试卷参考答案与评分标准
一.填空题(每小题4分,满分44分)
1.![]() ;2.
;2.![]() ; 3.
; 3.![]() ;4.
;4.![]() (
(![]() );5.
);5.![]() 或
或![]() ;6.
;6.![]() ;7.
;7.![]() ;
;
8.![]() ;9.
;9.![]() ;10.
;10.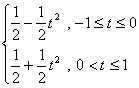 ;11.
;11.![]() .
.
二.选择题(每小题4分,满分16分)
12.B;13.D;14.C;15.B.
三.解答题(本大题满分90分)本大题共有6题,解答下列各题必须写出必要的步骤.
16.(本题满分12分)
解:由![]() 得
得![]() ,即
,即![]() ,……(3分)
,……(3分)
由![]() 得
得![]() , ……(7分)
, ……(7分)
即![]() ,又由
,又由![]() 得
得![]() ,……(10分)
,……(10分)
即![]() ,所以实数
,所以实数![]() 的取值范围是
的取值范围是![]() .……(12分)
.……(12分)
17.(本题满分14分.第(1)题6分,第(2)题8分)
解:(1)![]()
![]() , (3分)
, (3分)
∴ 函数![]() 的最大值是
的最大值是![]() ,此时
,此时![]() 的集合是
的集合是![]() .(6分)
.(6分)
(2)当![]() 时,
时,![]() , (8分)
, (8分)
则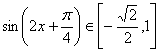 , (12分)
, (12分)
所以,函数![]() 的值域是
的值域是![]() . (14分)
. (14分)
18.(本题满分14分,第(1)题6分,第(2)题8分)
解:(1)当![]() 时,卡车从甲地到乙地行驶了
时,卡车从甲地到乙地行驶了![]() 小时 ……(2分)
小时 ……(2分)
所以,要耗油![]() (升)
(升)
答:当卡车以![]() 千米/小时的速度匀速行驶时,从甲地到乙地要耗油
千米/小时的速度匀速行驶时,从甲地到乙地要耗油![]() 升.…(6分)
升.…(6分)
(2)当卡车的速度为![]() 千米/小时,卡车从甲地到乙地行驶了
千米/小时,卡车从甲地到乙地行驶了![]() 小时,设耗油量为
小时,设耗油量为![]()
升,则![]() (
(![]() ),(10分)
),(10分)
配方得,![]() .
.
答:当卡车以![]() 千米/小时的速度匀速行驶时,从甲地到乙地耗油量最少,最少耗油量为
千米/小时的速度匀速行驶时,从甲地到乙地耗油量最少,最少耗油量为![]() 升. ……(14分)
升. ……(14分)
19.(本题满分14分.第(1)题4分,第(2)题10分)
解:(1)由题意,圆![]() 的半径
的半径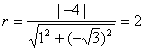 ,……(2分)
,……(2分)
圆![]() 的方程为
的方程为![]() . ……(4分)
. ……(4分)
(2)令![]() ,解得
,解得![]() ,
,![]() ,……(6分)
,……(6分)
设![]() ,由
,由![]() ,
,![]() ,
,![]() 成等比数列,得
成等比数列,得![]() ,
,
即![]() ,化简得
,化简得![]() ,……(8分)
,……(8分)
∴ ![]() ……(10分)
……(10分)
∵
点![]() 在圆
在圆![]() 内,∴
内,∴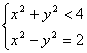 ,由此得
,由此得![]() .……(12分)
.……(12分)
∴ ![]() 的取值范围为
的取值范围为![]() .……(14分)
.……(14分)
20.(本题满分18分.第(1)题5分,第(2)题6分,第(3)题7分)
解:(1)由已知,当![]() 时,
时,![]() ,即
,即![]() .…(2分)
.…(2分)
![]()
![]() . ……(5分)
. ……(5分)
(2)解法一:由已知,当![]() 时,
时,![]() 是等差数列,公差为
是等差数列,公差为![]() ,数列递增.
,数列递增.
若![]() 是
是![]() 的最小值,则
的最小值,则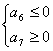 ,即
,即![]() ,得
,得![]() .……(7分)
.……(7分)
若![]() 是
是![]() 的最小值,则
的最小值,则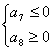 ,即
,即![]() ,得
,得![]() .……(9分)
.……(9分)
∴
当![]() 与
与![]() 两项中至少有一项是
两项中至少有一项是![]() 的最小值时,
的最小值时,![]() 的取值范围是
的取值范围是![]() .(11分)
.(11分)
(2)解法二:由(1), 当![]() 时,
时,![]() ,且
,且![]() 也满足
也满足
此式,
∵
在![]() 与
与![]() 两项中至少有一项是
两项中至少有一项是![]() 的最小值,
的最小值,
∴
![]() , ……(8分)
, ……(8分)
解得![]() ,从而
,从而![]() 的取值范围是
的取值范围是![]() .…(11分)
.…(11分)
(3)由(2)知![]() ,
,![]() ,26,…,
,26,…,![]() }
}
若![]() 是
是![]() 的最小值,则
的最小值,则![]() ,即
,即![]() ……(13分)
……(13分)
若![]() 是
是![]() 的最小值,
的最小值,![]() ,即
,即![]() ……(15分)
……(15分)
∴
![]() .……(18分)
.……(18分)
21.(本题满分18分.第(1)题4分,第(2)题6分,第(3)题8分)
解:(1)由![]() ,得
,得![]() ,
,![]() ,∵
,∵ ![]() ,∴
,∴ ![]() . ……(4分)
. ……(4分)
(2)由(1),![]() ,从而
,从而![]() ,只需研究
,只需研究![]() 在
在![]() 上的单调性.
上的单调性.
当![]() 时,
时,![]() .
.
设![]() ,且
,且![]() ,则
,则
![]() , …(6分)
, …(6分)
∵ ![]() ,∴
,∴ ![]() ,
,![]() ,
,![]() ,
,
∴ ![]() ,即
,即![]() .
.
∴ 函数![]() 在区间
在区间![]() 上是单调递增函数. ……(10分)
上是单调递增函数. ……(10分)
(3)原方程即为![]() ……①
……①
![]() 恒为方程①的一个解. ……(11分)
恒为方程①的一个解. ……(11分)
若![]() 时方程①有解,则
时方程①有解,则![]() ,解得
,解得![]() ,
,
由![]() ,得
,得 ![]() ; ……(13分)
; ……(13分)
若![]() 且
且![]() 时方程①有解,则
时方程①有解,则![]() ,解得
,解得![]() ,
,
由![]() 且
且![]() ,得
,得![]() 或
或![]() . ……(15分)
. ……(15分)
综上可得,当![]() 时,方程
时,方程![]() 有且仅有一个解;
有且仅有一个解;
当![]() 时,方程
时,方程![]() 有两个不同解;
有两个不同解;
当![]() 时,方程
时,方程![]() 有三个不同解. ……(18分)
有三个不同解. ……(18分)