金山区2007学年第一学期期末考试
高三数学理科测试试题
满分150分,完卷时间为120分钟,答案请写在答题纸上
一、填空题(每小题4分,共44分)
1、已知集合P={xx2–9<0},Q={yy=2x,xÎZ},则P∩Q = 。
2、若复数![]() 为实数,则实数
为实数,则实数![]() 。
。
3、函数f(x)=1+log 2 x(x≥2)的反函数f –1(x) = 。
4、函数![]() ,xÎ[4,6]的最小值
。
,xÎ[4,6]的最小值
。
5、若方程![]() 表示椭圆,则
表示椭圆,则![]() 的取值范围是
。
的取值范围是
。
6、方程sinx+cosx= –1在[0,π]内的解为 。
7、向量![]() 与
与![]() 的夹角为
的夹角为![]() ,
,![]() ,
,![]() ,则
,则![]() 。
。
8、直线![]() x+y–2
x+y–2![]() =0截圆x2+y2=4得的劣弧所对的圆心角的大小为 。
=0截圆x2+y2=4得的劣弧所对的圆心角的大小为 。
9、在实数等比数列{an}中a1+a2+a3=2,a4+a5+a6=16,则a7+a8+a9= 。
10、定义在R上的偶函数f(x),满足f(2+x) = f(2–x),且当xÎ[0,2]时,f(x)=![]() ,则f(2008)= 。
,则f(2008)= 。
11、正数数列{an}中,对于任意nÎN*,an是方程(n2+n)x2+(n2+n–1)x–1=0的根,Sn是正数数列{an}的前n项和,则![]() 。
。
二、选择题(每小题4分,共16分)
12、在复平面内,复数z=![]() 对应的点位于
( )
对应的点位于
( )
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
13、命题:“对任意的![]() ,
,![]() ”的否定是 ( )
”的否定是 ( )
(A)不存在![]() ,
,![]() ; (B)存在
; (B)存在![]() ,
,![]() ;
;
(C)存在![]() ,
,![]() ; (D)对任意的
; (D)对任意的![]() ,
,![]() .
.
14、已知A(1,0)、B(7,8),若点![]() 和点
和点![]() 到直线l的距离都为5,且满足上述条件的直线l共有n条,则n的值是
( )
到直线l的距离都为5,且满足上述条件的直线l共有n条,则n的值是
( )
(A) 1 (B) 2 (C) 3 (D) 4
15、 已知直线l:(m+1)x–my+![]() =0与圆C:x2+y2=2相切,且满足上述条件的直线l共有n条,则n的值为 ( )
=0与圆C:x2+y2=2相切,且满足上述条件的直线l共有n条,则n的值为 ( )
(A) 0 (B) 1 (C) 2 (D) 以上答案都不对
三、解答题(本大题满分90分)
16、(本大题12分)
设函数f(x)=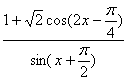 ,(1)化简f(x)的表达式,求f(x)的定义域,并求出f(x)的最大值和最小值;(2)若锐角a满足cosa=
,(1)化简f(x)的表达式,求f(x)的定义域,并求出f(x)的最大值和最小值;(2)若锐角a满足cosa=![]() ,求f(a)的值。
,求f(a)的值。
17、(本大题12分)
复数![]() 是一元二次方程ax2+bx+1=0(a、bÎR)的根,
是一元二次方程ax2+bx+1=0(a、bÎR)的根,
(1)求a和b的值;(2)若![]()
![]() ,求u。
,求u。
18、(本大题14分)
在△ABC中,a、b、c分别是角A、B、C的对边,且满足![]() ,
,
(1)求角B的度数;(2)若b=![]() ,a+c=5,求a和c的值。
,a+c=5,求a和c的值。
19、(本大题16分)
设![]() 为实数,函数f(x)=xx–a,其中xÎR。
为实数,函数f(x)=xx–a,其中xÎR。
(1)判断函数f(x)的奇偶性,并加以证明;(2)写出函数f(x)的单调区间。
20、(本大题18分)
阅读下面所给材料:已知数列{an},a1=2,an=3an–1+2,求数列的通项an。
解:令an=an–1=x,则有x=3x+2,所以x= –1,故原递推式an=3an–1+2可转化为:
an+1=3(an–1+1),因此数列{an+1}是首项为a1+1,公比为3的等比数列。
根据上述材料所给出提示,解答下列问题:
已知数列{an},a1=1,an=3an–1+4,
(1)求数列的通项an;并用解析几何中的有关思想方法来解释其原理;
(2)若记Sn=![]() ,求
,求![]() Sn;
Sn;
(3)若数列{bn}满足:b1=10,bn+i=100![]() ,利用所学过的知识,把问题转化为可以用阅读材料的提示,求出解数列{bn}的通项公式bn。
,利用所学过的知识,把问题转化为可以用阅读材料的提示,求出解数列{bn}的通项公式bn。
21、(本大题18分)
(1)已知平面上两定点![]() 、
、![]() ,且动点M的坐标满足
,且动点M的坐标满足![]() =0,求动点
=0,求动点![]() 的轨迹方程;
的轨迹方程;
(2)若把(1)的M的轨迹图像向右平移一个单位,再向下平移一个单位,恰与直线x+ky–3=0 相切,试求实数k的值;
 (3)如图1,l是经过椭圆
(3)如图1,l是经过椭圆![]() 长轴顶点A且与长轴垂直的直线,E、F是两个焦点,点PÎl,P不与A重合。若
长轴顶点A且与长轴垂直的直线,E、F是两个焦点,点PÎl,P不与A重合。若![]() ,证明:
,证明:![]() 。类比此结论到双曲线
。类比此结论到双曲线![]() ,
,![]() 是经过焦点
是经过焦点![]() 且与实轴垂直的直线,
且与实轴垂直的直线,![]() 是两个顶点,点PÎl,P不与
是两个顶点,点PÎl,P不与![]() 重合(如图2)。若
重合(如图2)。若![]() ,试求角
,试求角![]() 的取值范围。
的取值范围。
2007学年度第一学期高三数学期末考试试题答案(理)2008年1月
一、填空题:1、{–2, 0, 2} 2、2 3、2x–1 (x≥2) 4、5 5、–6<k<4且k¹–1
6、π 7、2 8、60o 9、128 10、2 11、1
二、选择题:12、A 13、C 14、C 15、B
三、解答题:
16、(1)函数f(x)= =![]() =
=![]() =2sinx+2cosx ……5分
=2sinx+2cosx ……5分
f(x)的定义域为{xx¹kπ+![]() ,kÎZ},……………………………………………………6分
,kÎZ},……………………………………………………6分
又f(x)=2![]() sin(x+
sin(x+![]() )……………………………………………………………………7分
)……………………………………………………………………7分
f(x)max=2![]() ,f(x)min=
–2
,f(x)min=
–2![]() ……………………………………………………………9分
……………………………………………………………9分
(2)若锐角a满足cosa=![]() ,则sina=
,则sina=![]() …………………………………………………10分
…………………………………………………10分
f(a)=![]() …………………………………………………………………………………12分
…………………………………………………………………………………12分
17、(1)由题得![]() ,…………………………………………………………2分
,…………………………………………………………2分
方程ax2+bx+1=0是实系数一元二次方程,故它的另一个根为![]() …………4分
…………4分
由韦达定理知: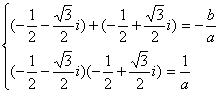 ,得
,得![]() ……………………6分
……………………6分
(2)由(1)知![]() ,设
,设 ![]() ……………………7分
……………………7分
则:![]() ,得
,得![]() ……8分
……8分
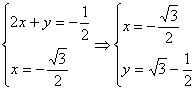 ,所以
,所以![]() ……………………12分
……………………12分
18、(1)由题![]() ,由正弦定理得:
,由正弦定理得:![]() ,……2分
,……2分
![]() ……………………………………………3分
……………………………………………3分
![]()
sin(B+C)+ 2cosB sinA=0 …………………………………………………………………4分
sinA+2cosB sinA=0……………………………………………(只要写出本行,给5分)5分
因为![]() ,所以cosB= –
,所以cosB= –![]() ,所以B=120o………………………………………7分
,所以B=120o………………………………………7分
(2)由余弦定理得:![]() ,………………………………………9分
,………………………………………9分
19=(a+c)2–
由![]() ,得
,得![]() 或
或![]() ………………………………(缺一解,扣1分)14分
………………………………(缺一解,扣1分)14分
19、(1)当a=0时,f(x)=xx,所以f(x)为奇函数…………………………………………1分
因为定义域为R关于原点对称,且f(–x)=–x–x=–f(x),所以f(x)为奇函数。……3分
当a¹0时,f(x)=xx–a为非奇非偶函数,………………………………………4分
f(a)=0,f(–a)=
–a
所以f(x)是非奇非偶函数。……………………………………………………………6分
(2)当a=0时,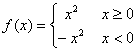 ,
,![]() 的单调递增区间为
的单调递增区间为![]() ;……8分
;……8分
当a>0时,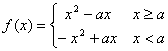
f(x)的单调递增区间为![]() 和
和![]() ;……………………………………10分
;……………………………………10分
f(x)的单调递减区间为![]() ;……………………………………………………12分
;……………………………………………………12分
当a<0时,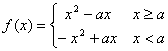
f(x)的单调递增区间为![]() 和
和![]() ;……………………………………14分
;……………………………………14分
f(x)的单调递减区间为![]() ………………………………………………………16分
………………………………………………………16分
20、(1) 令an=an–1=x,则有x=3x+4,所以x= –2,故原递推式an=3an–1+4可转化为:
an+2=3(an–1+2),因此数列{an+2}是首项为a1+2,公比为3的等比数列。
所以an+2=(a1+2)´3n–1,所以an=3n–2;…………………………………………2分
对于an=3an–1+4,可以看成把直线y=3x+4的方程改写成点斜式方程,
该点就是它与直线y=x的交点。……………………………………………………4分
(2)令dk=![]() =
=![]()
=(![]() )2
)2![]() =(
=(![]() )2(
)2(![]() –
–![]() )……………………………………………7分
)……………………………………………7分
Sn=![]() =d1+d2+……+dn
=d1+d2+……+dn
=(![]() )2[(
)2[(![]() )+(
)+(![]() )+(
)+(![]() )+……+(
)+……+(![]() )]
)]
=(![]() )2[
)2[![]() ]………………………………………………………………10分
]………………………………………………………………10分
![]() Sn=(
Sn=(![]() )2……………………………………………………………………12分
)2……………………………………………………………………12分
(3)数列{bn}满足:b1=10,bn+i=100![]() ,所以bn>0,lg bn+i=lg(100
,所以bn>0,lg bn+i=lg(100![]() )
)
令cn=lgbn,则cn+1=3cn+2,………………………………………………………14分
所以cn+2=3(cn–1+2),因此数列{cn+2}是首项为c1+2,公比为3的等比数列。
所以cn+2=(c1+2)´3n–1,所以cn=3n–2,…………………………………………16分
lgbn=cn=3n–2;bn=![]() …………………………………………………………18分
…………………………………………………………18分
21、(1)设![]() ,由
,由![]() 得
得![]() ,此即点
,此即点![]() 的轨迹方程。…3分
的轨迹方程。…3分
(2)将x2+y2=4向右平移一个单位,再向下平移一个单位后,
得到圆(x–1)2+(y+1)2=4…………………………………………………………………5分
依题意有![]() ,得k=0或
,得k=0或![]() ……………………………………………8分
……………………………………………8分
(3)(ⅰ)证明:不妨设点P在A的上方,并设![]() ,
,
则![]() ………………………………………10分
………………………………………10分
所以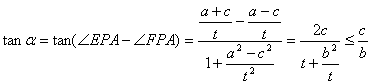 ……………12分
……………12分
所以![]() 。显然a为锐角,即:
。显然a为锐角,即:![]() ……………………14分
……………………14分
(ⅱ)不妨设点![]() 在
在![]() 的上方,并设
的上方,并设![]() ,
,
则![]() ,
,
所以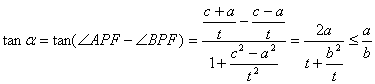
由于![]() 且
且![]() ,a为锐角,故
,a为锐角,故![]() 。……………18分
。……………18分