叙永一中高08级高三数学选修II测试题（2007.08）

一、选择题（每小题4分，共40分）

1．复数在复平面上对应的点位于（　　）

　　A．第一象限　　　　 B．第二象限　　　　　　C．第三象限　　　　 D．第四象限

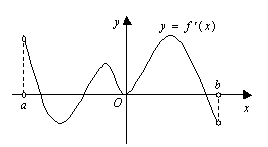
2．某次市教学质量检测，甲、乙、丙三科考试成绩的直方图如右图所示（由于人数众多，成绩分布的直方图可视为正态分布），则由如图曲线可得下列说法中正确的一个是（　　 ）

A．甲科总体的标准差最小　　　　　　　　　　　　　　

B．丙科总体的平均数最小

C．乙科总体的标准差及平均数都居中

D．甲、乙、丙的总体的平均数不相同

3．设ξ~N（0，1），且p(-3<ξ<3)=0.9974，则p(ξ≥3)=(　　　)

A.0.9974　　　　　 B.0.0026　　　　 C.0.0013　　　  D.0.0003

4. 函数的单调增区间是（　　　）

A. 　　　B. 与 　　C. 　　　 D.

	0	1	2	3
	0.1			0.1

5．设随机变量的分布列为右表所示且，

则（　　　 ）

A．0.2　　　　　　  B．0.1　

C．-0.2　　　　　　  D．-0.4

6．的值为（　　　 ）

A． 2　　　　 B． 0　　　　　  C． 1　　　　　 D． 不存在

7． 用数学归纳法证明“”时，从到，给等式的左边需要增乘的代数式是 (　　　)

A.　　　　　  B.　　　　 C.　　  D.

8．垂直于直线，且与曲线相切的直线方程是(　　  )

A．　　B．　　C．　　D．

9．下列各函数的导数，（1）

　 （4），其中正确的有（　　　　）

A．0个　　　　　　　　　　　　　 B．1个　　　　　　　　　　C．2个　　　　　　　　　　D．3个

10．函数的定义域为开区间，导函数在内的图象如图所示，则函数在开区间内有极小值点（　　　）

A．1个 　 B．2个 　　 C．3个　　　D． 4个

二、填空题（每小题4分，共20分）

11．一个公司有N个员工，下设一些部门，现采用分层抽样方法从全体员工中抽取一个容量为n的样本 (N是n的倍数)．已知某部门被抽取了m个员工，那么这一部门的员工数是　　　　　　　　　  ．

12、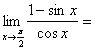　　　　 。13.曲线和在它们交点处的两条切线与轴所围成的三角形面积是　　　 ..

14．袋中有编号为1，2，3，4，5的五只小球，从中任取3只球，以ξ表示取出的球的最大号码，则E（ξ）的值是________.

15．关于函数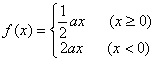，下列表述不正确的是　　　　　　　　  ．(填写答案序号)　　　　 

① 它是一个奇函数； ② 它在每一点都连续；③ 它在每一点都可导；④ 它是一个增函数； ⑤ 它有反函数．

三、解答题(每小题10分，共40分)

16． 设随机变量x 服从正态分布：x ~ N(1，2²)，试求：

(Ⅰ) ；　　　　(Ⅱ) 求常数c， 使 ．

参考数据：F(0)=0.5；F(1)=0.8413；F(2)=0.9772；F(0.5)= 0.6915；F(1.88)=0.9697；F(3)=0.9987．

17．某保险公司新开设了一项保险业务，若在一年内事件E发生，该公司要赔偿a元（但不退还保险金）．设在一年内E发生的概率为p，为使公司收益的期望值等于a的百分之十，公司应要求顾客交多少保险金？

18.设函数f(x)=2x³-3(a+1)x²+6ax+8，其中aÎR。

　  (1) 若f(x)在x=3处取得极值，求常数a的值；

(2) 若f(x)在(-¥,0)上为增函数，求a的取值范围。

19. 已知数列

证明

参考答案

DACAC　 ACACA

11、 12、0　 13、　14、4.5　 15、① ③ ④

16．解： (Ⅰ)　由=

==2=2=0.3830．

(Ⅱ)  由已知可得  ，∴　 ，

即　　，∴　 ，∴ ，  c=4.76．

17.解：设保险公司要求顾客交x元保险金，若以x表示公司每年的收益额，则x是一个随机变量，其分布列为：

x	x	x－a
P	1－p	p

因此，公司每年收益的期望值为Ex=x(1－p)+(x－a)·p=x－ap．

为使公司收益的期望值等于a的百分之十，只需Ex=0.1a，即x－ap=0.1a，

故可得x=(0.1+p)a．即顾客交的保险金为(0.1+p)a时，可使公司期望获益10%a．

18.解：（Ⅰ）

因取得极值，　所以　解得

经检验知当为极值点.

（Ⅱ）综上所述，当上为增函数.

19.解：（1）方法一 用数学归纳法证明：

1°当n=1时，

　 ∴，命题正确.

2°假设n=k时有

　 则

　

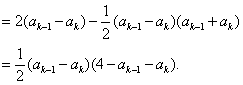
而

又

∴时命题正确.

由1°、2°知，对一切n∈N时有