高三数学阶段性检测
数学试题(选修物理学科卷)

一、填空题:(共14小题,每题5分,共计70分)
1.集合 ![]() 的元素个数是 ▲ .
的元素个数是 ▲ .
2.函数![]() 的最小正周期为_____▲_____.
的最小正周期为_____▲_____.
3.函数![]() 在(0,2)上是增函数且函数
在(0,2)上是增函数且函数![]() 是偶函数,请用“<”将
是偶函数,请用“<”将![]() 、
、
![]() 连接起来为_________▲_________.
连接起来为_________▲_________.
4.定义在R上的函数![]() 的值域是(0,2)则
的值域是(0,2)则![]() -1的值域为 ▲
.
-1的值域为 ▲
.
5.数列![]() 中,如果
中,如果![]() ,并且任意正整数
,并且任意正整数![]() 都有
都有![]() 成立,则
成立,则![]()
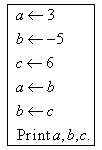 的值等于____▲___.
的值等于____▲___.
6.若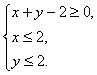 则
则![]() 的最大值与最小值之和为 ▲ .
的最大值与最小值之和为 ▲ .
7.已知 一个算法如右图:则输出后的![]() = ▲ .
= ▲ .
8.已知![]() 是圆
是圆![]() 上两点,
上两点,![]() 为坐标原点,且
为坐标原点,且
![]() ,则
,则![]() ▲ .
▲ .
9.向面积为S的△ABC内任投一点P,则随机事件△PBC的面积大于![]() 的概率为 ▲___.
的概率为 ▲___.
10.已知![]() {正实数},有不等式
{正实数},有不等式![]()
![]()
![]() ,依次类推可得一般结论________▲__________.
,依次类推可得一般结论________▲__________.
11.已知复数![]() ,
,![]() ,则复数
,则复数![]() 的虚部等于_ ▲____.
的虚部等于_ ▲____.
12.设![]()
![]() ,若A、B、C三点共线,且
,若A、B、C三点共线,且![]() ,则
,则![]() 的值为____▲____.
的值为____▲____.
13.若![]() …
…![]() 的方差为3,则
的方差为3,则![]() …
…![]() 的方差为 ▲ .
的方差为 ▲ .
14.直角坐标系中横坐标、纵坐标均为整数的点称为格点,如果函数![]() 的图象恰好通过
的图象恰好通过![]() (
(![]() ∈N*)个格点,则称函数
∈N*)个格点,则称函数![]() 为
为![]() 阶格点函数.下列函数:
阶格点函数.下列函数:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,
,
其中是一阶格点函数的有 ▲ (只填写符合条件的函数序号).
 二.解答题
二.解答题
15.(本题14分,)
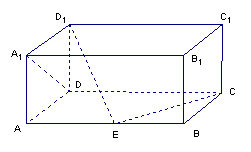
已知,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动
(Ⅰ)求证:无论点E在AB上的任何位置D1E⊥A1D
(Ⅱ)求三棱锥E-DD1C的体积。
16.(本题 14分) 已知![]() 。
。
(Ⅰ)试求![]() 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(Ⅱ)若![]() ,试求
,试求![]() 的值域。
的值域。
17.(15分)当实数![]() 变化时,直线
变化时,直线![]() :
:
![]() 与直线
与直线![]() 都过一个定点.
都过一个定点.
(Ⅰ)求出这个定点;
(Ⅱ)点![]() 在怎样的曲线上?求出这条曲线的方程,并写出该曲线的焦点坐标.
在怎样的曲线上?求出这条曲线的方程,并写出该曲线的焦点坐标.
18.(15分)已知f(x)=(x-1)![]() , g(x)=4(x-1),数列﹛an﹜中,对 任意正整数n,等
, g(x)=4(x-1),数列﹛an﹜中,对 任意正整数n,等
式(an+1-an)g(an)+f(an)=0都成立。且a1=2 当n≥2时 an≠1,设bn=an-1
(Ⅰ)求证数列﹛bn﹜是等比数列;
(Ⅱ)设Sn为数列﹛nbn﹜前n项和,Tn=Sn+![]() 求Tn的取值范围。
求Tn的取值范围。
19.(16分)某造船厂年最高造船量是20艘,已知造船x艘的产值函数为
![]() (单位:万元),成本函数为
(单位:万元),成本函数为![]() (单
(单
位:万元)。又在经济学中,函数![]() 的边际函数
的边际函数![]() 定义为:
定义为:
![]() 。求:
。求:
(Ⅰ)利润函数![]() 及边际利润函数
及边际利润函数![]() ;(提示:利润=产值-成本)
;(提示:利润=产值-成本)
(Ⅱ)年造船量安排多少艘时,可使造船厂的年利润最大?
(Ⅲ)求边际利润函数![]() 的单调递减区间,并说明单调递减在本题中的实际意义
的单调递减区间,并说明单调递减在本题中的实际意义
是什么?
20.(16分)设A![]() ,B
,B![]() 是函数
是函数![]() 图象上任意两点,且
图象上任意两点,且
![]() ,点M的横坐标为
,点M的横坐标为![]() 。
。
(Ⅰ)求证M点的纵坐标为定值;
(Ⅱ)若![]() ,且
,且![]() ,求
,求![]() ;
;
(Ⅲ)已知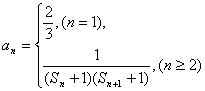 ,
,![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,
项和,
若![]() 对于一切
对于一切![]() 都成立,求
都成立,求![]() 的取值范围。
的取值范围。
数学(选修物理学科)加试题
(总分40分)
(第1题和第2题为必做题;第3-6题选做2题;10分![]() 4=40分)
4=40分)
一.必做题:(共2题每题10分,计20分)
1.求曲线![]() 直线
直线![]() 、
、![]() 轴围成的封闭图形的面积.
轴围成的封闭图形的面积.
2.如图,在直角梯形OABC中,∠COA=∠OAB=![]() ,OC=2,OA=AB=1。SO⊥平面OABC,SO=1,以OC,OA,OS分别为x轴、y轴、z轴建立空间直角坐标系O-xyz。
,OC=2,OA=AB=1。SO⊥平面OABC,SO=1,以OC,OA,OS分别为x轴、y轴、z轴建立空间直角坐标系O-xyz。
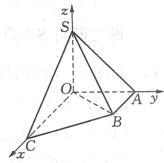 (Ⅰ)求
(Ⅰ)求![]() 与
与![]() 的夹角
的夹角![]() 的余弦值;
的余弦值;
(Ⅱ)设![]() ,满足
,满足![]() 平面SBC,求
平面SBC,求![]() 的坐标。
的坐标。
二.选题:(从3—6题 中任选2题每题 10分,共20分。如果多于2题以得分少的计分)
3. (选修4-5不等式选讲)已知a,b为正实数,![]() 求函数
求函数![]() 的最小值
的最小值
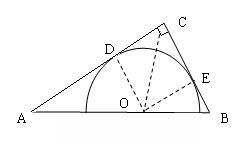
4.(选修4-1几何证明与选讲)半圆的圆心O在直角三角形ABC的斜边AB上,且半圆与两直角边相切.若斜边长为![]() ,半圆半径为
,半圆半径为![]() ,求直角三角形的面积S.
,求直角三角形的面积S.
5.(选修4-2矩阵与变换)求矩阵A=![]() 的逆矩阵.
的逆矩阵.
6. 求椭圆![]() 的中心坐标、焦点坐标、长轴和短轴的长,以及准线方程。
的中心坐标、焦点坐标、长轴和短轴的长,以及准线方程。