高三数学第一次月考试卷
数 学(文史类)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟.
参考公式: 正棱锥、圆锥的侧面积公式
如果事件A、B互斥,那么
![]()
P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么 其中,c表示底面周长、l表示斜高或
P(A·B)=P(A)·P(B) 母线长
如果事件A在1次实验中发生的概率是 球的体积公式
P,那么n次独立重复实验中恰好发生k
![]()
次的概率 其中R表示球的半径
![]()
第I卷(选择题 共50分)
一.选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合要求的.
1.设集合M={x|x2-x<0,x∈R![]() ,N={x||x|<2,x∈R
,N={x||x|<2,x∈R![]() ,则
,则
A.N ![]() M B.M∩N=M C.M∪N=M D.M∪N=R
M B.M∩N=M C.M∪N=M D.M∪N=R
2.已知向量a=(-1,![]() ),向量b=(
),向量b=(![]() ,-1),则a与b的夹角等于
,-1),则a与b的夹角等于
A.![]() B.
B.![]() C.
C.![]() π D.
π D.![]() π
π
3.已知函数f(x)=3x-1,则它的反函数y=f-1(x)的图象是
 A. B. C. D.
A. B. C. D.
4.若![]() ,则
,则![]() …
…![]() 的值为
的值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.“p或q为真命题”是“p 且q为真命题”的
A.充分不必要条件; B.必要不充分条件;
C.充要条件; D.既不充分又不必要条件![]()
6.曲线y=2x4上的点到直线y=-x-1的距离的最小值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.从P点引三条射线PA,PB,PC,每两条射线夹角为60°,则平面PAB和平面PBC所成二面角正弦值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
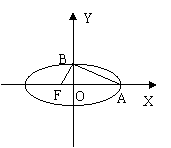 8.如图,椭圆中心在坐标原点,F为左焦点,当
8.如图,椭圆中心在坐标原点,F为左焦点,当![]() 时,其离心率为
时,其离心率为![]() ,此类椭圆被称为“黄金椭圆”.类比“黄金椭圆”可推算
,此类椭圆被称为“黄金椭圆”.类比“黄金椭圆”可推算
出“黄金双曲线”的离心率e等于
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.如果一个三位正整数的中间一个数字比另两个数字小,如305,414,879等,则称这个三位数为凹数,那么所有凹数的个数是
A.240 B.285 C.729 D.920
10.已知二次函数![]() ,当n依次取
,当n依次取![]() 时,其图像在x轴上所截得的线段的长度的总和为
时,其图像在x轴上所截得的线段的长度的总和为
A.1 B.![]() C.
C.![]() D.
D.![]()
二.填空题:本大题共5小题,每小题5分,共25分,把答案填在题中横线上.
11.已知x,y满足约束条件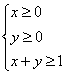 ,则z=x+2y的最小值为
.
,则z=x+2y的最小值为
.
12.已知函数![]() =
=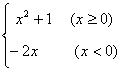 ,则
,则![]() .
.
13.设![]() ,则直线
,则直线![]() 的倾斜角是
.
的倾斜角是
.
14.从圆的10等分点中任取3个点,可组成一个三角形. 现从这10个点任取3个点,要构成直角三角形的概率是 .
15.观察下列的图形中小正方形的个数,则(i)第6个图中有 个小正方形,
(ii)第n个图中有 个小正方形.
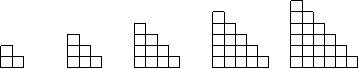
三.解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.
16.(本小题满分12分)已知函数![]() .(1)求函数
.(1)求函数![]()
的单调递增区间;(2)若将![]() 的图象按向量
的图象按向量![]() 平移后,再将所有点的横坐标缩小到原来的
平移后,再将所有点的横坐标缩小到原来的![]() 倍,得到函数
倍,得到函数![]() 的图象,试写出
的图象,试写出![]() 的解析式
的解析式![]()
 17.(本小题满分12分)在一次军事演习中,某军同时出动了甲、乙、丙三架战斗机对一军事目标进行轰炸,已知甲击中目标的概率是
17.(本小题满分12分)在一次军事演习中,某军同时出动了甲、乙、丙三架战斗机对一军事目标进行轰炸,已知甲击中目标的概率是![]() ;甲、丙同时轰炸一次,目标未被击中的概率为
;甲、丙同时轰炸一次,目标未被击中的概率为![]() ;乙、丙同时轰炸一次,都击中目标的概率是
;乙、丙同时轰炸一次,都击中目标的概率是![]() .(1)求乙、丙各自击中目标的概率;(2)求目标被击中的概率.
.(1)求乙、丙各自击中目标的概率;(2)求目标被击中的概率.
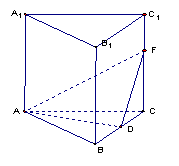
18.(本小题满分12分)直三棱柱ABC-A1B1C1中AB=AC=AA1=3a,
BC=2a,D是BC的中点,F是C1C上一点,且CF=2a.
(1)求证:B1F⊥平面ADF;
(2)求平面ADF与平面AA1B1B所成角的正弦值.
19.(本小题满分12分){an},{bn}都是各项为正数的数列,对任意的正自然数n,都有an、bn2、an+1成等差数列,bn2、an+1、bn+12成等比数列.(1)试问{bn}是否是等差数列?为什么?
(2)求证:对任意的正自然数p,q(p>q),bp-q2+bp+q2≥2bp2成立;(3)如果a1=1,b1=![]() ,
,
Sn=![]() ,求Sn.
,求Sn.
20.(本小题满分13分)已知动点P与双曲线![]() =1的两个焦点F1、F2的距离之和为定值,且cosF1PF2的最小值为-
=1的两个焦点F1、F2的距离之和为定值,且cosF1PF2的最小值为-![]() .(1)求动点P的轨迹方程;(2)若已知D(0,3),M、N在动点P的轨迹上,且
.(1)求动点P的轨迹方程;(2)若已知D(0,3),M、N在动点P的轨迹上,且![]() =λ
=λ![]() ,求实数λ的取值范围.
,求实数λ的取值范围.
21.(本小题满分14分)已知![]() 是定义在R上的函数,其图象交x轴于A、B、C三点
是定义在R上的函数,其图象交x轴于A、B、C三点![]() 若点B的坐标为(2,0),且f(x)在[-1,0]和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性
若点B的坐标为(2,0),且f(x)在[-1,0]和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性![]() (1)求c的值;(2)在函数f(x)的图象上是否存在一点M(x0,y0),使得f(x)在点M的切线斜率为3b?若存在,求出点M的坐标;若不存在,请说明理由;(3)求AC 的取值范围.
(1)求c的值;(2)在函数f(x)的图象上是否存在一点M(x0,y0),使得f(x)在点M的切线斜率为3b?若存在,求出点M的坐标;若不存在,请说明理由;(3)求AC 的取值范围.
数 学(文史类)参考答案
1. B 2.C 3 D 4 B 5. B 6.D 7.A 8.A 9.B 10.B
二.填空题:本大题共5小题,每小题5分,共25分,把答案填在题中横线上.
11.1
12.5
13. ![]() .
.
14.
![]() .
.
15. ![]()
16.
解:(1)∵f(x)=2![]() cos2x-2sinxcosx-
cos2x-2sinxcosx-![]() =
=![]() (cos2x+1)-sin2x-
(cos2x+1)-sin2x-![]() =2cos(2x+
=2cos(2x+![]() )
)
![]() .…………6分
.…………6分
(2)f(x)=2cos(2x+![]() )
)![]()
![]() ∴g(x)=2cos(4x+
∴g(x)=2cos(4x+![]() ).…………12分
).…………12分
17
解:(1)记甲、乙、丙各自独立击中目标的事件分别为A、B、C.
则由已知,得P(A)=![]() ,P(
,P(![]() ·
·![]() )=P(
)=P(![]() )P(
)P(![]() )=
)=![]() [1-P(C)]=
[1-P(C)]=![]() ,∴P(C)=
,∴P(C)=![]() ………3分
………3分
由P(B·C)=P(B)P(C)=![]() ,得
,得![]() P(B)=
P(B)=![]() ,∴P(B)=
,∴P(B)=![]() . …………8分
. …………8分
(2)目标被击中的概率为
1-P(![]() ·
·![]() ·
·![]() )=1-[1-P(A)][1-P(B)][1-P(C)]=1-(1-
)=1-[1-P(A)][1-P(B)][1-P(C)]=1-(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )=
)=![]() ,………10分
,………10分
答:(1)乙、丙各自击中目标概率分别为![]() ,
,![]() ;(2)目标被击中的概率为
;(2)目标被击中的概率为![]() .………12分
.………12分
 18.
18.
解:法1 (1)因为AB=AC,D是BC的中点,所以AD⊥BC.
又平面CC1B1B⊥ABC ,
则AD⊥平面CC1B1B. B1F 在平面CC1B1B内, AD⊥B1F.
……………………………………………………………3分
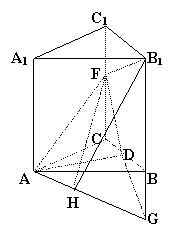 在矩形CC1B1B中
在矩形CC1B1B中
tan∠C1B1F=tan∠CFD=![]() ,所以∠C1B1F=∠CFD ,
,所以∠C1B1F=∠CFD ,
∠C1FB1+∠CFD=∠C1FB1+∠C1B1F=900,
因此FD⊥B1F ,即证B1F⊥平面ADF;………………6分
(2)延长FD,B1B交于G,则AG为所求二面角的棱.
由RtΔFCD≌RtΔGBD,所以CF=GB=2a.过B1作B1H⊥
AG,且B1H与AG交于H.又 B1F⊥平面ADF,FH⊥AG,
∠B1HF为所求二面角的平面角. ……………………9分
由RtΔABG∽RtΔB1HG ,解得B1H =![]() .而
.而
B1F=![]() , =
, =![]() ,sin∠B1HF=
,sin∠B1HF=![]() ,
,
即所求二面角的正弦值是![]() . ……………12分
. ……………12分
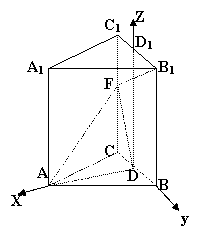
法2:以D为坐标原点,DA![]() DB
DB![]() DD1分别为x
DD1分别为x![]() y
y![]() z轴建立空间直角坐标
z轴建立空间直角坐标
系(D1是C1B1的中点),易知A(2![]() a,0,0), B(0,a,0) ,F(0,-a,2a), B1(0,a,3a), …3分
a,0,0), B(0,a,0) ,F(0,-a,2a), B1(0,a,3a), …3分
![]() ,
, ![]() ,
,![]() ,由
,由![]()
 且
且![]() ,得B1F⊥DF, B1F⊥DA,即B1F⊥平面ADF; …………6分
,得B1F⊥DF, B1F⊥DA,即B1F⊥平面ADF; …………6分
(2)由(1)知![]() ,
,![]() ,
,
设平面AA1B1B的一个法向量为![]() ,则
,则
![]() 且
且![]() ,
,
可取![]() ,…9分
,…9分
由cos<![]() ,
,![]() >=
>=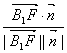 =-
=-![]() 得,
得,
sin<![]() ,
,![]() >=
>=![]() .即所求值
.即所求值![]() .…………12分
.…………12分
19.
解:依题意2bn2=an+an+1, ① an+12=bn2·bn+12. ②
(1)∵an>0,bn>0,∴由②式得an+1=bn·bn+1,从而n≥2时,an=bn-1·bn,
代入①2bn2= bn-1bn+bnbn+1,
∴2bn=bn-1+bn+1(n≥2),∴{bn}是等差数列.…………………………………………4分
(2)因为{bn}是等差数列,∴bp-q+bp+q=2bp.
∴bp-q2+bp+q2≥![]() . …………………………………………8分
. …………………………………………8分
(3)由a1=1,b1=![]() 及①②两式易得a2=3,b2=
及①②两式易得a2=3,b2=![]() ,
,
∴{bn}中公差d=![]() ,∴bn=b1+(n-1)d=
,∴bn=b1+(n-1)d=![]() (n+1),
(n+1),
∴an+1=![]() (n+1)(n+2). ③
(n+1)(n+2). ③
又a1=1也适合③,∴an=![]() (n∈N),∴
(n∈N),∴![]() ,
,
∴Sn=2[1-![]() ]=2(1-
]=2(1-![]() ), ……………………12分
), ……………………12分
20.
解:(1)由题意c2=5,设PF1+PF2=2a(a>![]() ),由余弦定理
),由余弦定理
得cosF1PF2=![]() =
=![]() -1.
-1.
又PF1·PF2≤(![]() )2=a2, …………………………………………3分
)2=a2, …………………………………………3分
当且仅当PF1=PF2时,PF1·PF2取最大值,
此时cosF1PF2取最小值![]() -1,令
-1,令![]() -1=-
-1=-![]() ,解得a2=9.
,解得a2=9.
∵c=![]() ,∴b2=4,故所求P的轨迹方程为
,∴b2=4,故所求P的轨迹方程为![]() =1………………………………6分
=1………………………………6分
(3)设N(s,t),M(x,y),则由![]() =λ
=λ![]() ,可得
,可得
(x,y-3)=λ(s,t-3),故x=λs,y=3+λ(t-3), …………………………………9分
∵M、N在动点P的轨迹上,故![]() =1且
=1且![]() +
+![]() =1.
=1.
消去s,可得![]() =1-λ2,
=1-λ2,
解得t=![]() .又t≤2,∴
.又t≤2,∴![]() ≤2,解得
≤2,解得![]() ≤λ≤5.
≤λ≤5.
故实数λ的取值范围是[![]() ,5]. ………………………………………………13分
,5]. ………………………………………………13分
21.
解:(1)![]() ,依题意
,依题意![]() 在
在![]() 和[0,2]上有相反的单调性,
和[0,2]上有相反的单调性,
∴x=0是f(x)的一个极值点,故![]() ,得c=0 …………………………3分
,得c=0 …………………………3分
(2)因为f(x)交x轴于点B(2,0),
∴![]() ,即
,即![]() …………………………………………5分
…………………………………………5分
令![]() 得
得![]()
因为f (x)在[0,2]和[4,5]上有相反的单调性,∴![]() 在[0,2]和[4,5]上有相反的符号,故2≤
在[0,2]和[4,5]上有相反的符号,故2≤![]() ≤4Þ-6≤
≤4Þ-6≤![]() ≤-3 ……………………………………7分
≤-3 ……………………………………7分
假设存在点M(x0,y0)使得f (x)在点M的切线斜率为3b,则f /(x0)
=3b,
即![]() ,
,![]()
而-6≤![]() ≤-3,∴△<0,
≤-3,∴△<0,
故不存在点M(x0,y0),使得f (x)在点M的切线斜率为3b.……………………9分
(3)设![]() ,依题意可令
,依题意可令![]()
![]()
则![]() 即
即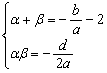 ……………………………………11分
……………………………………11分
∴![]()
∵-6≤![]() ≤-3,∴当
≤-3,∴当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,故3≤ AC ≤4
,故3≤ AC ≤4![]()
![]() …………………………14分
…………………………14分