高三数学第一学期第一次摸底考试 科目：数学 班级：中六
姓名： 成绩: 家长签署：
一、选择题：本大题共8小题，每小题5分，共40分。
1．已知集合
，则集合
=（ ）.
A．{
} B．{
} C．{
} D．{
}
2．复数
的共轭复数是（ ）.
A．
B．
C．
D．
3. “
”是“A=30º”的（ ）.
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
4．原命题：“设
、
、
，若
则
”的逆命题、否命题、逆否命题真命题共有（ ）.
A．0个 B．1个 C．2个 D．3个
5. 不等式x2-x+a<0的解集为(-1,2),则实数a的值等于( )
A.8 B.2 C.-2 D.-8
6．等差数列
中，
，那么
的值是（ ）.
A． 12 B． 24 C．16 D． 48
7．甲、乙两人下棋，甲获胜的概率是40%，甲不输的概率为90%，则甲、乙二人下成和棋的概率为（ ）.
A．60% B．30% C．10% D．50%
8. 右图是
年中央电视台举办的挑战主持人大赛上，七位评委为某选手打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的平均数和方差分别为（ ）.
A．
，
B．，
C．
， D．，
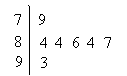
二．填空题：本大题6个小题，每小题4分，共24分。
9．已知x、y
R
，且4x+3y=1，则
＋
的最小值为______________.
10．函数
的定义域是 ，单调递减区间是___________
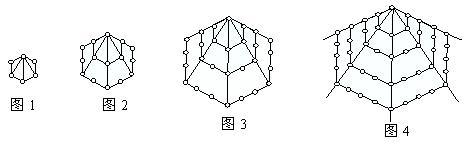
11. 在一次珠宝展览会上，某商家展出一套珠宝首饰，第一件首饰是1颗珠宝， 第二件首饰是由6颗珠宝(图中圆圈表示珠宝)构成如图1所示的正六边形， 第三件首饰如图2， 第四件首饰如图3， 第五件首饰如图4， 以后每件首饰都在前一件上，按照这种规律增加一定数量的珠宝，使它构成更大的正六变形，依此推断第6件首饰上应有_______________颗珠宝，第
件首饰所用珠宝总数为_________________颗.
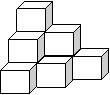12. 棱长为1 cm的小正方体组成如图所示的几何体，那么这个几何体的表面积是 
.
13．计算
=_________。
14. 已知地f(x)=
,则f—1(1)= _________。
三.解答题
15.(2
)-
×(-1
)-5-(
)0÷(0.5)-5+0.0016-0.75 (6分)
16.(10分) 小明、小华用4张扑克牌（分别是黑桃2、黑桃4，黑桃5、梅花5）玩游戏，他们将扑克牌洗匀后，背面朝上放在桌面上，小明先抽，小华后抽，抽出的牌不放回，各抽一张.
（1）若小明恰好抽到黑桃4；
①请绘制出这种情况的树状图；②求小华抽出的牌的牌面数字比4大的概率.
（2）小明、小华约定：若小明抽到的牌的牌面数字比小华的大，则小明胜，反之，则小明负，你认为这个游戏是否公平，说明你的理由.
17.(10分)已知
，
．
（1）当
时，求证：
在
上是减函数；
（2）如果对
不等式
恒成立，求实数的取值范围
18.(10分)某机床厂今年年初用98万元购进一台数控机床，并立即投入生产使用，计划第一年维修、保养费用12万元，从第二年开始，每年所需维修、保养费用比上一年增加4万元，该机床使用后，每年总收入为50万元，设使用x年后数控机床的盈利额为y万元.
（1）写出y与x之间的函数关系式；
（2）从第几年开始，该机床开始盈利（盈利额为正值）
（3）使用若干年后，对机床的处理方案有两种：
（i）当年平均盈利额达到最大值时，以30万元价格处理该机床；
（ii）当盈利额达到最大值时，以12万元价格处理该机床。
问用哪种方案处理较为合理？请说明理由.
数学参考答案
一.C．A．B．B．C．B．D．C
二9.7+4
10 .
；
11.66,2n2-n; 12.36 13.3-3i 14. 2
三.15.124
16. 解：（1）① 小明抽出的牌 小华抽出的牌 结果
2
（4，2）
4
5
（4，5）
5
（4，5）
② 由①可知小华抽出的牌面数字比4大的概率为：
.
（2）小明获胜的情况有：（4，2）、（5，4）、（5，4）、（5，2）、（5，2）, 故小明获胜的概率为：
， 因为
，所以不公平.
17. 解：（1）当时，
，
∵
，∴在上是减函数.
（2）∵不等式恒成立，即不等式
恒成立，
∴不等式
恒成立. 当
时， 
不恒成立；
当
时，不等式恒成立，即
，∴
.
当
时，不等式
不恒成立. 综上，的取值范围是
18. 解：（1）依题得：
（2）解不等式
（3）（i）
当且仅当
时，即x=7时等号成立。
到2014年，年平均盈利额达到最大值，工厂共获利12×7+30＝114万元。
（ii）
故到2017年，盈利额达到最大值，工厂获利102+12＝114万元
因为盈利额达到的最大值相同，而方案Ⅰ所用的时间较短，故方案Ⅰ比较合理.