高三文科数学第三次月考试卷
一.选择题(共10×5=50分)
1、设![]() ,
,![]() ,则
,则![]() 等于( D
)
等于( D
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2、函数![]() 的反函数的定义域为( B )
的反函数的定义域为( B )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3、在等比数列![]() (
(![]() )中,若
)中,若![]() ,
,![]() ,则该数列的前10项和为( B
)
,则该数列的前10项和为( B
)
A.![]() B.
B.![]()
![]() C.
C.![]() D.
D.![]()
4、已知![]() 的值为( C
)
的值为( C
)
A.-2
B.![]() C.
C.![]() D.2
D.2
5、椭圆![]() 的焦点为
的焦点为![]() ,
,![]() ,两条准线与
,两条准线与![]() 轴的交点分别为
轴的交点分别为![]() ,若
,若![]() ,则该椭圆离心率的取值范围是( D )
,则该椭圆离心率的取值范围是( D )
A.![]() B.
B.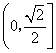 C.
C.![]() D.
D.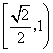
6、若不等式组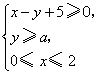 表示的平面区域是一个三角形,则
表示的平面区域是一个三角形,则![]() 的取值范围是( C )
的取值范围是( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 或
或![]()
7、由点M(5,3)向圆![]() 所引切线长是( A )
所引切线长是( A )
A.![]() B.
B. ![]() C. 51
D . 1
C. 51
D . 1
8、不等式![]() 的解集不是空集,则实数a的取值范围是( C
)
的解集不是空集,则实数a的取值范围是( C
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9、P是双曲线![]() 的右支上一点,M、N分别是圆(x+5)2+y2=4和(x-5)2+y2=1上的点,则PM-PN的最大值为( D )
的右支上一点,M、N分别是圆(x+5)2+y2=4和(x-5)2+y2=1上的点,则PM-PN的最大值为( D )
A. 6 B.7 C.8 D.9
10、已知偶函数y=f(x)在[-1,0]上为单调递减函数,又![]() 、
、![]() 为锐角三角形的两内角,则 ( A
)
为锐角三角形的两内角,则 ( A
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二.填空题(共5×5=25分)
11、若![]() 则向量
则向量![]() 与
与![]() 的夹角为
的夹角为 ![]() 。
。
12、已知![]() 为椭圆E的两个左右焦点,抛物线C以
为椭圆E的两个左右焦点,抛物线C以![]() 为顶点,
为顶点,![]() 为焦点,设P为椭圆与抛物线的一个交点,如果椭圆离心率e满足
为焦点,设P为椭圆与抛物线的一个交点,如果椭圆离心率e满足![]() ,则e的值为
,则e的值为 ![]()
13、若![]() 的焦点坐标为 (0, ±3)
的焦点坐标为 (0, ±3)
14、对于函数f(x)定义域中任意的x1,x2(x1≠x2),考查如下结论:
①![]() ;
②
;
②![]() ;
;
③![]() ; ④
; ④![]() .
.
当![]() 时,上述结论中正确结论的序号是 ① ③ ④ 。(写出全部正确结论的序号)
时,上述结论中正确结论的序号是 ① ③ ④ 。(写出全部正确结论的序号)
15、在实数集R上定义运算![]() 对任意实数x恒成立,则实数a的取值范围是
对任意实数x恒成立,则实数a的取值范围是 ![]() .
.
三.解答题(共12+12+12+12+13+14=75分)
16.(满分12分)记关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,不等式
,不等式![]() 的解集为
的解集为![]() .
.
(1)若![]() ,求
,求![]() ; (2)若
; (2)若![]() ,求正数
,求正数![]() 的取值范围
的取值范围
解:(1)由![]() ,得
,得![]() .---------------6分
.---------------6分
(2)![]() .---------------8分
.---------------8分
由![]() ,得
,得![]() ,---------------------10分
,---------------------10分
又![]() ,所以
,所以![]() ,
,
即![]() 的取值范围是
的取值范围是![]() .------------------------12分
.------------------------12分
17.(满分12分)设向量![]() ,向量
,向量![]() 垂直于向量
垂直于向量![]() ,向量
,向量![]() 平行于
平行于![]() ,试求
,试求![]() 的坐标.
的坐标.
解:设![]() ,∴
,∴![]() , ∴
, ∴![]() ①---------4分
①---------4分
又![]() 即:
即:![]() ②---------8分
②---------8分
联立①、②得![]() ∴
∴
![]() .----------12分
.----------12分
18.(满分12分)已知![]() 是三角形
是三角形![]() 三内角,向量
三内角,向量![]() ,且
,且![]()
(1)求角![]() ;
(2)若
;
(2)若![]() ,求
,求![]() 。
。
解:(1)∵![]() ∴
∴![]() 即
即![]()
![]() ,
, ![]()
∵![]() ∴
∴![]() ∴
∴![]() ------------6分
------------6分
(2)由题知![]() ,整理得
,整理得![]()
∴![]() ∴
∴![]() ∴
∴![]() 或
或![]()
而![]() 使
使![]() ,舍去 ∴
,舍去 ∴![]() --------------12分
--------------12分
(它法类比给分)
19.(满分12分)设![]()
(1)确定a的值,使![]() 为奇函数;
为奇函数;
(2)当![]() 是奇函数时,设
是奇函数时,设![]() 为函数
为函数![]() 的反函数,则对给定的正实数k,求使
的反函数,则对给定的正实数k,求使![]() 的取值范围。
的取值范围。
解: (1)由![]()
![]() -----------------5分
-----------------5分
(2)![]() --------------------7分
--------------------7分
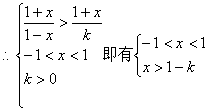 -----------------10分
-----------------10分
![]() -----------------12分
-----------------12分
20.(满分13分)已知数列![]() 满足递推关系式
满足递推关系式![]()
(Ⅰ)求![]()
| |
解:(1)由![]() 知
知![]()
解得:![]() 同理得
同理得![]() ……………………4分
……………………4分
(2)![]()
![]()
![]()
即![]() 构成以
构成以![]() 为首项,以1为公差的等差数列,……………………6分
为首项,以1为公差的等差数列,……………………6分
![]()
![]()
![]() …………………………8分
…………………………8分
(3)![]()
![]()
![]()
![]()
![]() …………………………13分
…………………………13分
21.(满分14分)已知椭圆![]() 的左焦点为F,O为坐标原点。
的左焦点为F,O为坐标原点。
(1)求过点O、F,并且与椭圆的左准线![]() 相切的圆的方程;
相切的圆的方程;
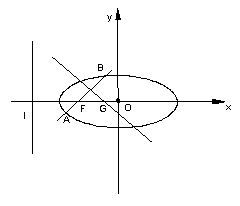
(2)设过点F且不与坐标轴垂直的直线交椭圆于A、B两点,线段AB的垂直平分线与![]() 轴交于点G,
轴交于点G,
求点G横坐标的取值范围。
解:(1)![]() -----------2分
-----------2分
![]() 圆过点O、F,
圆过点O、F, ![]() 圆心M在直线
圆心M在直线![]() 上。 ------------3分
上。 ------------3分
 设
设![]() 则圆半径
则圆半径 ![]()
由![]() 得
得![]()
解得![]()
![]() 所求圆的方程为
所求圆的方程为![]() ----------6分
----------6分
(2)设直线AB的方程为![]()
代入![]() 整理得
整理得
![]() ------------------9分
------------------9分
![]() 直线AB过椭圆的左焦点F,
直线AB过椭圆的左焦点F,![]() 方程有两个不等实根。
方程有两个不等实根。
记![]() 中点
中点![]()
则![]()
![]() 的垂直平分线NG的方程为
的垂直平分线NG的方程为![]() ------------------------11分
------------------------11分
令![]() 得
得
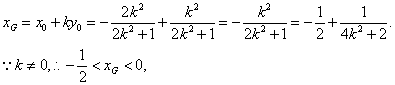
![]() 点G横坐标的取值范围为
点G横坐标的取值范围为![]() ------------------------------14分
------------------------------14分