高一级1月月考数学试题(文科)
第I卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个备选项中,只有一项是符合题目要求的。
1、已知向量![]() ,向量
,向量![]() ,且
,且![]() ,则
,则![]() =( )
=( )
A、9 B、6 C、5 D、1
2、已知集合![]() ,集合
,集合![]() ,则( )
,则( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3、求以抛物线![]() 的焦点为焦点,且离心率为
的焦点为焦点,且离心率为![]() 的椭圆的标准方程为( )
的椭圆的标准方程为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、已知等差数列![]() 满足:
满足:![]() ,若等比数列
,若等比数列![]() 满足
满足![]() ,则
,则![]() 为( )
为( )
A、16 B、32 C、64 D、27
5、![]() 的图象相邻两对称轴之间的距离为(
)
的图象相邻两对称轴之间的距离为(
)
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6、抛物线![]() 在点
在点![]() 处的切线与其平行直线
处的切线与其平行直线![]() 间的距离是( )
间的距离是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
7、在![]() (O为原点)中,
(O为原点)中,![]() ,
,![]() ,若
,若![]() ,则
,则![]() 的值为( )
的值为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
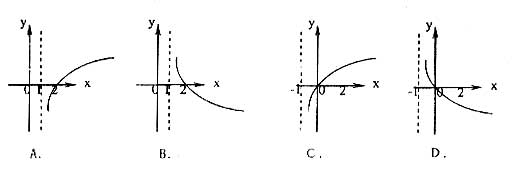
8、若函数![]() (
(![]() 且
且![]() )在
)在![]() 上既是奇函数,又是增函数,则
上既是奇函数,又是增函数,则![]() 的图像是( )
的图像是( )
9、已知![]() 的三个角分别为A,B,C,满足
的三个角分别为A,B,C,满足![]() ,则
,则![]() 的值为( )
的值为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10、设双曲线M:![]() ,过点C
,过点C![]() 且斜率为1的直线,交双曲线的两渐近线于A,B两点,若2
且斜率为1的直线,交双曲线的两渐近线于A,B两点,若2![]() ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
11、已知![]() ,且满足
,且满足![]() ,设
,设![]() 的最大值是( )
的最大值是( )
A、![]() B、4
C、
B、4
C、![]() D、5
D、5
12、函数![]() 满足:对一切
满足:对一切![]() ,
,![]() ;当
;当![]() 时,
时,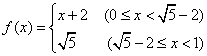 ,则
,则![]() ( )
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
第II卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分。把答案填写在答题卡相应位置上。
13、以坐标原点为圆心且与直线![]() 相切的圆方程为
相切的圆方程为
14、已知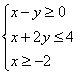 ,则
,则![]() 的最小值为
的最小值为
15、已知函数![]() 的反函数为
的反函数为![]() (
(![]() 且
且![]() ),则函数
),则函数![]() 必过定点
必过定点
16、如右图,它满足
 ①第
①第![]() 行首尾两数均为
行首尾两数均为![]()
②表中的递推关系如杨辉三角,
则第![]() 行
行![]() 的第二个数是
的第二个数是
三、解答题:本大题共6小题,共76分。解答应写出文字说明、证明过程或演算步骤。
17、(13分)已知向量![]() ,记
,记![]()
(1)求![]() 的周期;
的周期;
(2)若![]() ,则求
,则求![]() 的最小值
的最小值
18、(13分)解不等式![]() (
(![]() 且
且![]() )
)
19、(12分)已知偶函数![]() ,对任意
,对任意![]() ,恒有
,恒有![]() ,
,
求(1)![]() 的值;
的值;
(2)![]() 的表达式
的表达式
(3)令![]() (
(![]() 且
且![]() ),求
),求![]() 在
在![]() 上的最值
上的最值
20、(12分)某商场因管理不善及场内设施陈旧,致使年底结算亏损,决定从今年开始投入资金进行调整,计划第一个月投入80万元,以后每月投入将比上月减少![]() 。第一个月的经营收入约40万元,预计以后每个月收入会比上个月增加
。第一个月的经营收入约40万元,预计以后每个月收入会比上个月增加![]() (1)设
(1)设![]() 个月内的总投入为
个月内的总投入为![]() 万元,总收入为
万元,总收入为![]() 万元,写出
万元,写出![]() ,
,![]() (2)问经过几个月后商场开始扭亏为盈。
(2)问经过几个月后商场开始扭亏为盈。
21、(12分)已知A![]() ,B
,B![]() ,C
,C![]() 三点在椭圆
三点在椭圆![]() 上,
上,![]() 的重心与此椭圆的右焦点
的重心与此椭圆的右焦点![]() 重合
重合
(1)求椭圆方程
(2)求BC的方程
22、(12分)抛物线![]() 的准线与
的准线与![]() 轴的交点为M,过点M作直线交抛物线于A、B两点.
轴的交点为M,过点M作直线交抛物线于A、B两点.
(1)求线段AB中点的轨迹方程;
(2)若线段AB的垂直平分线交对称轴于点N![]() ,求证:
,求证:![]() ;
;
(3)若直线![]() 的斜率依次取
的斜率依次取![]() 时,线段AB的垂直平分线与抛物线对称轴的交点依次是
时,线段AB的垂直平分线与抛物线对称轴的交点依次是![]() ,求
,求
![]()