高中毕业班第一次模拟考试试卷数学(理科)

高中毕业班第一次模拟考试试卷数学(理科)

本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试时间

120分钟.

第Ⅰ卷（选择题，共60分）

一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的。）

1、使不等式成立的一个必要不充分条件是

　　　 A.　　　　　 B．.

　　　 C．.　　　　D.

2、设命题p：若a>b，则<；命题q：<0<0。给出下列四个复合命题：①p或q；②p且q；③p且q；④p或q。其中真命题的个数有

(A)0个　　 (B)1个　　 (C)2个　　 (D)3个

3、已知复数z满足z²+3=0，则z³的值为

(A)　 (B)3　 (C)3　 (D)

4、已知两平行平面间的距离为3，点P为平面内的动点，边长为1的正ABC在平面内，则三棱锥P-ABC的体积为

(A)　 (B)　　　　  (C)　　　　　(D)　

5、．已知函数f(x)=x³+bx²+cx+d ,x[-1,2],若对任意x₁，x₂[-1,2](其中x₁ x₂)，都有[>0成立，则b+c

(A)有最大值　　　　  (B)有最大值-　(C) 有最小值　 (D)有最小值 -　

6、已知等差数列{a_n}的前n项和为S_n ，若S₂=8，S₅=35，则过点P（n,a_n+1）和Q(n+2,a_n+2+1)()的直线的一个方向向量的坐标可以是

(A)　(1，-2)　 (B) (2， 　)　　 (C) (--，-1　)　　 (D)　(-2，--　)

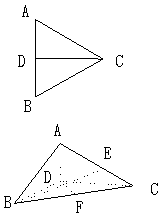
7、在正ABC中，CD为AB边上的高，E、F分别为边AC、BC的中点，将ABC沿CD翻折成直二面角A—DC—B(如图)，则异面直线BE与DF所成的角为

(A)arccos　　 (B)arcsin　　 

(C) arccos(- )　(D), arcsin(-)

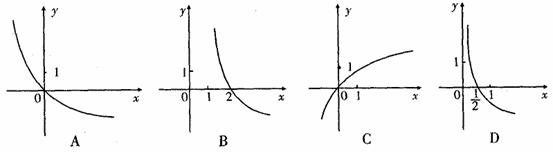
8、若函数f(x)=a^x(a>0且a1),并且f(2)<0，则函数f(x+1)的图象可能是

9、已知曲线y=2sin(x+)cos(-x)与直线y=相交，若在y轴右侧的交点自左向右依次记为P₁,P₂,P₃,……则等于

(A)　 (B)2　 (C)3　 (D)4

10、设集合M={(x,y)(x+1)²＋y²=1, x,y∈R}, N={(x,y)x+y-c0, x,y∈R},则使得MN=M的c的取值范围是

(A)[--1,)　　　(B)(- ,--1]　 (C)[ +1, )　 (D)(- ,+1]

11、已知双曲线M：双曲线的左右焦点分别为F₁、F₂，P为双曲线上一点，且的最小值的取值集合是[-3a²,-a²]，则双曲线M的离心率的取值范围是

(A)[2,4]　　 (B)[,2]　 (C)　 [,4)　　 (D)　 (1, ]

12、某单位举行庆祝活动已经确定了8个节目的节目单。开演前，又需增加外单位3个节目，其中两个独唱，一个小品，若将这3个节目插入原节目单中，则外单位的节目不排在节目单的第一个和最后一个，且2个独唱节目不连续演出的概率为

(A) 　　　(B) 　　 (C) 　　(D)　  

第Ⅱ卷（非选择题，共90分）

二、填空题(本大题共4个小题，每小题4分，满分16分。)

13、设1＋(1+x)＋(1+2x)²＋(1+3x)³ … ＋ 1+nx)ⁿ= a₀+ a₁x+ a₂x², ()

则=_____________

14、已知随机变量ξ 只能取3个值：x₁ ， x₂ ， x_3，其概率依次成等差数列，则这个等差数列公差的取值范围是_______

15、已知数列是公差为d的等差数列，其前n项和为s_n，则有s_m+n=s_m+s_n+mnd， 类似的，对于公比为q的等比数列来说，设其前n项积为T_n，则关于T_m+n、T_m、T_n及q的一个关系式为______________

16、已知定义在R上的奇函数y=f(x)满足f(x+2)=f(x)+f(1)，当x(-1,1)时，f(x)=x，则函数y=f(x)的图象与y=log₃x的图象的交点个数是__________。

三、解答题：（本大题共6小题，共74分，解答题应写出文字说明、证明过程或演算步骤。）

17、(本小题满分12分)

　 已知锐角ABC中，内角A、B、C的对边分别为a、b、c，向量

(Ⅰ)求角B的大小；

(Ⅱ)若b=3，求AC边上的高的最大值。

18、(本小题满分12分)

某大学开设甲、乙、丙三门选修课，学生是否选修哪门课互不影响，已知某学生只选修甲的概率为0.08，只选修甲和乙的概率为0.12，至少选修一门的概率是0.88，用ξ表示该学生选修的课程门数和没有选修的课程门数的乘积。

(Ⅰ)记“函数f(x)=x²+ξx为R上的偶函数”为事件A，求事件A的概率；

(Ⅱ)求ξ的分布列和数学期望

19、(本小题满分12分)

已知直四棱柱ABCD—A₁B₁C₁D₁中，底面ABCD为直角梯形，AB∥CD，∠ADC=90

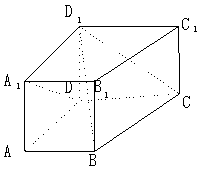AD=AA₁=1，CD=kAB=2,k>1。　　　　　　　　　　　　

(Ⅰ)求证：A₁DD₁B；　　　　　　　　　　

(Ⅱ)当k=2时，求点B到面ACD₁的距离；　　　　 

(Ⅲ)当k为何值时，二面角D₁-CB-D的大小为

20、(本小题满分12分)

　已知函数，e为自然对数的底数。

(Ⅰ)求函数y=f(x)的单调区间；

(Ⅱ)设a>0，g(x)=-(a²+2a)e^x-1，x[-2,1]，总存在x₂[0,4]，使得g(x₁)-g(x₂)=0成立，求a的取值范围。

21、(本小题满分12分)

　　已知点P在椭圆E：上，F₁、F₂分别为椭圆E上左、右焦点，满足

(Ⅰ)求椭圆E的离心率；

(Ⅱ)若椭圆E的长轴长为6，过定点Q(m,0)(其中-3<m<3,且m0)的直线l与椭圆E相交于两个不同点M、N，且。在x轴上是否存在定点G，使得。若存在，求出所有满足这种条件的点G的坐标；若不存在，说明理由。

22、(本小题满分14分)

已知数列满足：a₁=a(aR)。对于n=1,2,3…..，有;

(Ⅰ)当0<<4时，证明：0<；

(Ⅱ)若a满足0<a<1,求数列的通项;

(Ⅲ)证明：满足的自然数n存在。

参考答案