高中数学第三学期末教学质量测试
试 题
本试卷分为试题卷和答题卷两部分，其中试题卷由第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）组成，共3页；答题卷共4页.满分100分.考试结束后将答题卡和答题卷一并交回.
第Ⅰ卷(选择题,共48分)
注意事项:
1．答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.
2．每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其它答案,不能答在试题卷上.
一.选择题:本大题共12小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的,把它选出来填涂在答题卡上.
1.已知a、b、c、d∈R，且ab>0,
<
,则下列各式中成立的是
A.bc<ad
B.bc>ad
C.
>
D.<
2．过点
的直线l与x轴、y轴的正半轴分别交于P、Q两点，且
，
则直线l的方程为
A.x+2y-4=0 B.x-2y=0 C.x-y-1=0 D.x+y-3=0
3.已知抛物线
（
）的准线与圆
相切，且此抛物线上的点
到焦点的距离等于3，则m=
A.±
B.±
C.±1
D.0
4.在直径为d的圆的内接矩形中,面积最大的是 ,且这个内接矩形的面积等于
A.非正方形的矩形,
d2
B.正方形,d2
C.非正方形的矩形,d2 D.正方形,d2
5.方程
所对应的曲线图形是
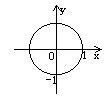
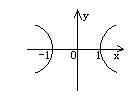
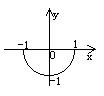
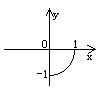
A． B． C． D．
6.斜率为1的直线与双曲线
相交于A、B两点，且AB中点的横坐标为1,则线段AB的长为
A.
B.
C.
D.3
7.有两排座位,前排11个座位,后排12个座位.现安排2人就座,规定前排中间的3个座位不能坐,并且这2人不左右相邻,那么不同排法的种数是
A.234 B.346 C.350 D.363
8.已知
、
是椭圆
(
)的两个焦点,P是椭圆上的一点,若
=90º,则
的面积是
.那么题目中所空缺的条件可能是
A.a=
b>0
B.a=
b>0
C.a=b>0
D.a=b>0
9.若z=
满足约束条件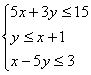
,则z的最大值与最小值之和为
A.29 B.7 C.28 D.6
10.已知A、B是抛物线y2＝2px（p>0）上的两个点，O为坐标原点，若OA＝OB，且△AOB的垂心恰是抛物线的焦点，则直线AB的方程为
A.x=p
B. x=
p
C.x=
p D.x=3p
11.已知圆C与圆(x－1)2＋y2＝1关于直线y＝－x对称，则圆C的方程为
A.(x＋1)2＋y2＝1 B.x2＋y2＝1
C.x2＋(y＋1)2＝1 D.x2＋(y－1)2＝1
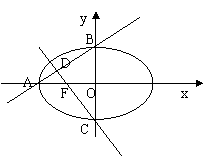12. 如图所示，椭圆
的离心率
,左焦点为F,A、B、C为其三个顶点，直线CF与AB交于D，则
的值等于
A.
B.
C.
D.
第Ⅱ卷(非选择题,共52分)
注意事项:
1.用钢笔或圆珠笔将答案直接写在答题卷上.
2.答卷前将答题卷的密封线内项目填写清楚.
二.填空题:本大题共4小题,每小题3分,共12分.把答案填在题中横线上.
13.
展开式的常数项是
.（用数字作答）
14.在一次口试中,要从10道题中随机抽出3道题进行回答,答对了其中2道题就获得及格.某考生会回答10道题中的6道题,那么他(她)不及格的概率是 .
15.已知双曲线的中心在原点，离心率为
，若它的一条准线与抛物线
的准线重合，则该双曲线与抛物线y2＝4x的交点到原点的距离是
.
16.已知A、B、C三点的坐标分别是(0,-2)、(0,0)、(3,1),若点M满足
,点N满足
，点P满足
，则P点的轨迹方程是
.
三.解答题:本大题共4小题,共40分.解答应写出文字说明、证明过程或演算步骤.
17.（本题满分10分）解不等式: 
.
18.（本题满分10分）甲、乙两人各射击一次，击中目标的概率分别是
和
假设两人射击是否击中目标，相互之间没有影响；每次射击是否击中目标，相互之间没有影响.
（1）求甲射击4次，至少1次未击中目标的概率；
（2）求两人各射击4次，甲恰好击中目标2次且乙恰好击中目标3次的概率；
（3）假设某人连续2次未击中目标,则停止射击.问:乙恰好射击5次后，被中止射击的概率是多少？
19.（本题满分10分）在双曲线
的一支上有不同的三点A（
,
），B(
,6),C(
,
)与焦点F(0,5)的距离成等差数列.
(1)求+;
(2)求证:线段AC的垂直平分线经过某一定点,并求出定点的坐标.
20.（本题满分10分）已知A是圆
上任一点，AB垂直于x轴，交x轴于点B．以A为圆心、AB为半径作圆交已知圆于C、D，连结CD交AB于点P.
(1)求点P的轨迹方程;
(2)若(1)所求得的点P的轨迹为M,过点Q(
,0)作直线l交轨迹M于E、G两点，O为坐标原点，求△EOG的面积的最大值，并求出此时直线l的倾斜角.