高三联考理科数学试题
一、选择题（本大题共10小题，每小题5分，共50分）
1、
A、1 B、
C、
D、不存在
2、设R为全集，集合A＝
，B＝
，那么
等于
A、
B、
C、
D、
3、若命题p的否命题是q，q的逆命题是r，则r是p的
A、逆否命题 B、否命题 C、逆命题 D、以上判断都不对
4、已知y＝f(x)的图象关于点（－1，0）对称，且当
时，f(x)＝
，则当
时，f(x)的解析式为
A、
B、－
C、－ D、
5、在
内，使0＜sinx＋cosx＜1成立的的取值范围是
A、
B、
C、
D、
6、在一个45°的二面角的一个面内有一条直线与二面角的另一个面所成的角为30°，则此直线与二面角棱所成的角为
A、30° B、45° C、60° D、90°
7、一块实验地分成5垄，分别种植5种不同的农作物，且甲种农作物既不能与乙种农作物相邻，也不能与丙种农作物相邻，则不同的种植方法有
A、24种 B、36种 C、48种 D、60种
8、对于任意两个正数m、n，定义运算
：当m、n都为偶数或都为奇数时，mn＝
；当m、n为一奇一偶时，mn＝
；设集合A＝
，则集合A中的元素个数是
A、14 B、15 C、16 D、17
9、从30名男生和20名女生中抽出10人组成一个调查小组，若按性别依比例分层抽样，则不同的抽样方法有
A、
B、
C、
D、
10、已知函数
，x∈（－1,1），当
时，a的取值范围是
A、（－2，1） B、（0，
） C、（0，1） D、（－2，）
二、填空题（本大题5小题，每小题4分，共20分）
11、设
，则f(2006)的值为
12、已知直线l被椭圆
所截得的弦的中点为（4，2），则l被椭圆截得的弦长为
13、
的展开式中含x3项的系数为
14、已知平面上三个单位向量
、
、
相互之间的夹角为120°，则向量－，－的夹角为
15、一个正方体的箱子棱长为2，将8个直径为1的铁球放进去后，则正中央能放下的最大球的直径是
三、解答题（本大题共6小题，共80分，解答应写出文字说明，证明过程或演算步骤）
16、（本小题满分12分）
已知函数
的定义域是
，值域为[－2，1]，若向量
满足
，求n的取值范围
17、（本小题满分12分）
市特警队员进行手枪实弹射击考核，每次射出一发子弹，每射击5发为一组，一旦命中就停止，并转入下一组考核，否则一直打完5发子弹才能转入下一组考核，已知新队员小李每射击一次的命中概率为0.8，且每次射击命中与否互不影响
（1）若队员完成连续两组考核所用子弹不超过3发，则可被评为优秀射手，求小李被评为优秀射手的概率；
（2）求小李在一组考核中所用子弹数ξ的分布列，并求ξ的期望
18、（本小题满分14分）
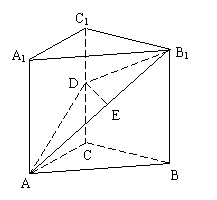如图，已知直三棱柱A1B1C1－ABC的底面是等腰三角形，底角∠BAC＝30º，且AC＝AA1＝a，D是C1C中点
（1）求证：面AB1D⊥面A1ABB1；
（2）求C1到面AB1D的距离
19、（本小题满分14分）
已知数列｛an｝的前n项的平均数为2n＋1
（1）求｛an｝的通项公式；
（2）设
，试判断并说明
的符号；
（3）设函数
，是否存在最大的实数k，当
时，对于一切非零自然数n，都有
20、（本小题满分14分）
已知函数
（1）若函数f(x)在x＝2时取得极值，求a的值；
（2）若函数f(x)在闭区间[－1，1]上的最大值为g(a)，求g(a)的解析式
21、（本小题满分14分）
已知抛物线C：
，直线l：y＝kx＋b（b≠0），直线l与抛物线C交于A、B两点（A在y轴左侧）
（1）若
（O为坐标原点），且ΔAOB的重心在直线
上，求实数，b的值；
（2）若k＝1，b＝2，若过A、B的圆
与抛物线C在A处有相同的切线，求圆的方程
参考答案
一、CBACC BBDDC
二、11、－2 12、
13、－8
14、60° 15、
16、化简得 
m＝1 解得
17、（1）0.896
（2）
| ξ | 1 | 2 | 3 | 4 | 5 |
| P | 0.8 | 0.16 | 0.032 | 0.0064 | 0.0016 |
Eξ=1.2496
18、（2）
19、（1）
（2）
（3）存在实数k=1
20、(1)a＝4
(2)
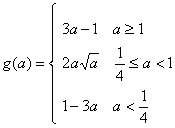
21、（1）k＝b＝1 （2）
