高三数文科学调研联考试题
本试题分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。共150分。考试时间120分钟。
参考公式:
如果事件![]() 、
、![]() 互斥,那么
互斥,那么![]()
如果事件![]() 、
、![]() 相互独立,那么
相互独立,那么![]()
如果事件![]() 在一次试验中发生的概率是
在一次试验中发生的概率是![]() ,那么
,那么![]() 次独立重复试验中恰好发生
次独立重复试验中恰好发生![]() 次的概率是
次的概率是![]()
球的体积公式 ![]() ,球的表面积公式
,球的表面积公式![]() ,其中
,其中![]() 表示球的半径
表示球的半径
第Ⅰ卷(选择题,共50分)
一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知全集U = {1,2,3,4,5,6,7},A = {3,4,5},B = {1,3,6},则A∩(![]() )等于 ( )
)等于 ( )
A.{4,5} B.{2,4,5,7} C.{1,6} D.{3}
2.函数y=![]() 的定义域为( )
的定义域为( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
3.为了得到函数![]() ,
,![]() 的图像,只需把函数
的图像,只需把函数![]() ,
,![]() 的图像上所有的点( )
的图像上所有的点( )
A、向左平移![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的![]() 倍(纵坐标不变)
B、向右平移
倍(纵坐标不变)
B、向右平移![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的![]() 倍(纵坐标不变)
倍(纵坐标不变)
C、向左平移![]() 个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
D、向右平移![]() 个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
4.以直线y= -x+1与坐标轴的交点为焦点的抛物线的标准方程为( )
A x2=-4y或y2=-4x B x2=4y或y2=4x
C x2=2y或y2=2x D x2=2y或y2=-2x
5.若![]() 、
、![]() 是两条不重合直线,
是两条不重合直线,![]() 、
、![]() 是两个不重合的平面,则
是两个不重合的平面,则![]() ∥
∥![]() 的一个充分而不必要条件是:( )
的一个充分而不必要条件是:( )
A ![]() ,
,![]() ,
,![]() ∥
∥![]() 且b∥
且b∥![]() B
B ![]() ,
,![]() ,且a∥b
,且a∥b
C ![]() ,
,![]() ,且
,且![]() ∥
∥![]() D
D ![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,且a∥b
,且a∥b
6.在等差数列![]() 中,
中,![]() ,
,![]() ,若
,若![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A 60 B 62 C 70 D 72
7.定义: ![]() ×
×![]() =
= ![]()
![]() sin
sin![]() ,其中
,其中![]() 为向量
为向量![]() 与
与![]() 的夹角,若
的夹角,若 ![]() = 2,
= 2, ![]() = 5,
= 5,![]() ·
·![]() = – 6,则
= – 6,则 ![]() ×
×![]() =( )
=( )
A.-8 B. 8 C.8或 – 8 D.6
|
8.在某城市中,A、B两地有如图所示道路网,从A地到B地
最近的走法有( )种
A 8 B 9 C 10 D 12
9.将进货单价为8元的商品按10元一个销售时,每天可卖出100个,若此商品的销售单价每再涨1元,日销售量就减少10个,为了获取最大利润,此商品的销售单价应定为( )元
A 12 B 13 C 14 D 15
10. 一个三棱锥S-ABC的三条侧棱SA、SB、SC两两互相垂直,且长度分别为1,![]() ,3,已知该三棱锥的四个顶点都在一个球面上,则这个球的表面积为( )
,3,已知该三棱锥的四个顶点都在一个球面上,则这个球的表面积为( )
A 16π B 32π C 36π D 64π
第Ⅱ卷(非选择题 共100分)
二、填空题:本大题共5个小题,每小题4分,共20分
11.某个班有45名学生,学校为了解他们的身体发育状况,决定分成男生、女生两部分采用分层抽样,现每个女生被抽取的概率为0.2 ,抽取了3 名女生,则男生应抽取 人
12. 已知变量![]() 、
、![]() 满足
满足![]() 则z=x+y-2的最大值为__________。
则z=x+y-2的最大值为__________。
13.若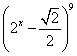 的展开式的第7项为
的展开式的第7项为![]() ,则x=
,则x=
14.曲线y=2x2上的点到直线y= -x-1的距离的最小值为
15.对于一切实数x,令[x]为不大于x的最大整数,则函数![]() 称为高斯函数或取整函数,如 f(2.1)=2;若
称为高斯函数或取整函数,如 f(2.1)=2;若![]() 为数列
为数列![]() 的前n项和,则
的前n项和,则![]() =
=
三、解答题:本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤
16.(本小题满分12分)
已知![]()
求(1)sinα,cosα的值;(2)求![]() 的值
的值
17. (本小题满分12分)
有A,B,C,D四个城市,它们都有一个著名的旅游点依此记为a,b,c,d把A,B,C,D和a,b,c,d分别写成左、右两列,现在一名旅游爱好者随机用4条线把左右全部连接起来,构成“一一对应”,已知连接一个城市与该城市的旅游点正确的得2分,连错的得0分
(1)求该旅游爱好者得分的可能值;
(2)将该旅游爱好者得k分的概率记为P (k), 求P (k)
18.(本小题满分14分)
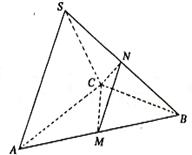 在三棱锥S—ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2
在三棱锥S—ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2![]() ,M、N分别为AB、SB的中点.
,M、N分别为AB、SB的中点.
(1)证明:AC⊥SB;
(2)求二面角N—CM—B的大小;
(3)求点B到平面CMN的距离.
19.(本小题满分14分)
已知公差不为0的等差数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]()
![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 成等比数列,
成等比数列,![]() 满足
满足![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和
20.(本小题满分14分)
在直角坐标系中,O为坐标原点,设直线![]() 经过点
经过点![]() ,且与
,且与![]() 轴交于点
轴交于点![]()
(I)求直线![]() 的方程;
的方程;
(II)如果一个椭圆经过点![]() ,且以点
,且以点![]() 为它的一个焦点,求椭圆的标准方程;
为它的一个焦点,求椭圆的标准方程;
(III)若在(I)、(II)、情形下,设直线![]() 与椭圆的另一个交点为
与椭圆的另一个交点为![]() ,且
,且![]() ,当
,当![]() 最小时,求
最小时,求![]() 对应的值。
对应的值。
21.(本小题满分14分)
已知函数![]() ,
, ![]() 为其图像上任意一点,过点
为其图像上任意一点,过点![]() 的切线的斜率
的切线的斜率![]() ,且函数
,且函数![]() 有极小值1,
有极小值1,
(1)求函数![]() 的表达式及其函数
的表达式及其函数![]() 的极大值.
的极大值.
(2)当-2≤x≤4时,讨论方程f(x)=m的解的个数
参考答案
一、选择题
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答 案 | A | C | C | B | C | B | B | C | C | A |
二、填空题
11 6
12 1
13 ![]()
14 ![]() 15
15 ![]()
三、解答题
16(1)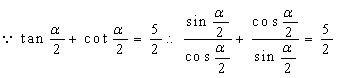
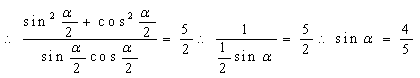 ………6分
………6分
又![]() ………8分
………8分
(2)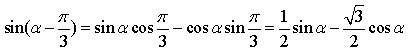
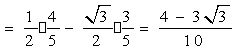 ………12分
………12分
17
(1) 该旅游爱好者得分的可能值为0分,2分,4分,8分 ………4分
(2)
k=0时, 连对的个数为0个,则![]() ………6分
………6分
k=2时, 连对的个数为1个,则![]() ………8分
………8分
k=4时, 连对的个数为2个,则![]() ………10分
………10分
k=8时, 连对的个数为4个,则![]() ………12分
………12分
18. 解:(1)取AC中点D,连结SD、DB.
∵SA=SC,AB=BC,
∴AC⊥SD且AC⊥BD,
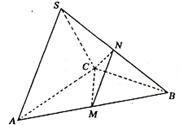 ∴AC⊥平面SDB,又SB
∴AC⊥平面SDB,又SB![]() 平面SDB,
平面SDB,
∴AC⊥SB ………4分
(2)∵AC⊥平面SDB,AC![]() 平面ABC,
平面ABC,
∴平面SDB⊥平面ABC.
过N作NE⊥BD于E,NE⊥平面ABC,
过E作EF⊥CM于F,连结NF,
则NF⊥CM.
∴∠NFE为二面角N-CM-B的平面角 ………6分
∵平面SAC⊥平面ABC,SD⊥AC,∴SD⊥平面ABC.
又∵NE⊥平面ABC,∴NE∥SD.
∵SN=NB,
∴NE=![]() SD=
SD=![]() =
=![]()
![]()
![]() =
=![]() ,
且ED=EB.
,
且ED=EB.
在正△ABC中,由平几知识可求得EF=![]() MB=
MB=![]() ,
,
在Rt△NEF中,tan∠NFE=![]() =2
=2![]() ,
,
∴二面角N—CM—B的大小是arctan2![]() ………10分
………10分
(3)在Rt△NEF中,NF=![]() =
=![]() ,
,
∴S△CMN=![]() CM·NF=
CM·NF=![]()
![]() ,
,
S△CMB=![]() BM·CM=2
BM·CM=2![]() -------------11分
-------------11分
设点B到平面CMN的距离为h,
∵VB-CMN=VN-CMB,NE⊥平面CMB,
∴![]() S△CMN·h=
S△CMN·h=![]() S△CMB·NE,∴h=
S△CMB·NE,∴h=![]() =
=![]() .
.
即点B到平面CMN的距离为![]() ………14分
………14分
19
(1)当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]()
![]() .
.
![]() 是等差数列,
是等差数列,
![]() ,
, ![]() ············4分
············4分
(2) ∵![]() ∴
∴![]()
∴![]() ∴ p=0 或
∴ p=0 或![]() ············6分
············6分
当p=0时,数列的公差为0与已知矛盾,所以![]() ∴
∴ ![]()
∵![]() ∴
∴![]() ············8分
············8分
∴![]() ∴
∴![]() ············10分
············10分
∴ ![]() =3
=3![]()
![]() =3
=3![]()
上式相减得![]()
∴![]() ············14分
············14分
20
(1)![]()
![]() 根据两点式得,所求直线
根据两点式得,所求直线![]() 的方程为
的方程为 ![]()
即 ![]() 。
。
![]() 直线
直线![]() 的方程是
的方程是![]() ……………4分
……………4分
(2)解:设所求椭圆的标准方程为![]()
![]()
![]() 一个焦点为
一个焦点为![]()
![]() 即
即 ![]() ①…………6分
①…………6分
![]() 点
点![]() 在椭圆
在椭圆![]()
![]()
![]()
![]() 上,
上,
![]()
![]() ②
②
由①②解得 ![]()
所以所求椭圆的标准方程为 ![]() ………9分
………9分
(3)由题意得方程组
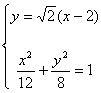 解得
解得 ![]() 或
或![]()
![]()
![]()
![]()
![]()
![]()
![]() 当
当![]() 时,
时,![]() 最小。
…………14分
最小。
…………14分
21![]() ………… 1分
………… 1分
![]()
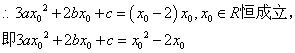
![]()
![]() ………… 5分
………… 5分
![]()
![]()
![]()
![]() ………… 8分
………… 8分
(2)由(1)知f(x)在![]()
![]() 是增函数,(0,2)上是减函数,
是增函数,(0,2)上是减函数,
易得m=1或![]() 时两个根;m
时两个根;m![]() 三个根;
三个根;
![]() 或
或![]() 一个解,其他无解 ………… 14分
一个解,其他无解 ………… 14分
