高三数学训练卷(一)
本试卷共150分 考试时间120分钟
一、选择题(本大题共12小题;每小题5分,共60分)
1. 以下可以估计总体稳定性的统计量是 ( )
A. 样本平均数 B. 样本中位数 C. 样本方差 D. 样本最大值
2. 函数![]() y的反函数是
( )
y的反函数是
( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
3. 若向量n与直线l垂直,则称向量n为直线l的法向量. 直线![]() 的一个法向
的一个法向
量为 ( )
A. ![]() B.
B.
![]() C.
C. ![]() D.
D.
![]()
4. 设等差数列![]() 的前n项的和是
的前n项的和是![]() ,且
,且![]() ,则
( )
,则
( )
A. ![]() B.
B.
![]() C.
C. ![]() D.
D.
![]()
5. 已知![]() 的三个顶点在同一球面上,
的三个顶点在同一球面上,![]() 若球心
若球心![]() 到平面
到平面![]() 的距离为1,则该球的半径为
( )
的距离为1,则该球的半径为
( )
A. 1
B. ![]() C.
C.
![]() D. 2
D. 2
6. 当![]() 时,函数
时,函数![]() 的最小值为
( )
的最小值为
( )
A. ![]() B. 3
C.
B. 3
C. ![]() D. 4
D. 4
7. 若函数![]() 的最小正周期为1,则它的图象的一个对称中心为
的最小正周期为1,则它的图象的一个对称中心为
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
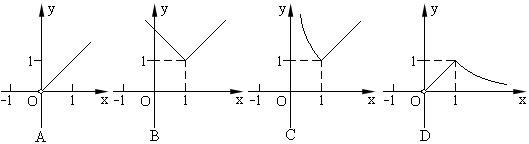
8. 函数![]() 的图像大致是
( )
的图像大致是
( )
9. “![]() ”是“直线
”是“直线![]() 与圆
与圆![]() 相切”的
( )
相切”的
( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
10. 已知函数![]() 满足
满足![]() ,且当
,且当![]() 时,
时,![]() . 设
. 设
![]() ,则
( )
,则
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
11. 若M是直线![]() 上到原点的距离最近的点,则当
上到原点的距离最近的点,则当![]() 在实数范围内变化时,动点M的轨迹是
( )
在实数范围内变化时,动点M的轨迹是
( )
A. 直线 B. 线段 C. 圆 D. 椭圆
12. 将三种作物种植在如图5块试验田里,每块种植一种作物,且同一种作物在相邻的试验田中,不同的种植方法有 ( )
![]()
A. 24种 B. 36种
C. 42种 D. 48种
二、填空题(本大题共6小题;每小题4分,共24分)
13. 设集合![]() ,
,![]() . 若
. 若![]() ,则
,则![]() .
.
14. 设周期为4的奇函数![]() 的定义域为R,且当
的定义域为R,且当![]() 时,
时,![]() ,则
,则![]() 的值为
.
的值为
.
15. 已知双曲线的中心在坐标原点O,焦点在y轴上,它的虚轴长为2,且焦距是两准线间距
离的2倍,则该双曲线的方程为 .
16. 设![]() 且
且![]() . 若
. 若![]() ,则的值为
.
,则的值为
.
17. 在![]() 中,若
中,若![]() ,则
,则![]() 的值为
.
的值为
.
18. 已知![]() ,
,![]() ,
,![]() . 若将坐标平面沿x轴折成直二面角,则折后
. 若将坐标平面沿x轴折成直二面角,则折后
![]() 的余弦值为
.
的余弦值为
.
三、解答题(本大题共5小题,共66分)
19. (本小题满分12分)
一位学生每天骑自行车上学,从他家到学校有5个交通岗,假设他在交通岗遇到红灯是相互独立的,且首末两个交通岗遇到红灯的概率均为p ,其余3个交通岗遇到红灯的概率均为![]() .
.
(1)
若![]() ,求该学生在第三个交通岗第一遇到红灯的概率;
,求该学生在第三个交通岗第一遇到红灯的概率;
(2)
若该学生至多遇到一次红灯的概率不超过![]() ,求p的取值范围.
,求p的取值范围.
20. (本小题满分12分)
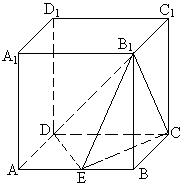
如图,在正方形![]() —
—![]() 中,
中,![]() 为
为![]() 的中点.
的中点.
(1) 求![]() 和
和![]() 所成的角
所成的角
(2) 证明:平面![]()
![]() 平面
平面![]() ;
;
(3) 求二面角![]() —
—![]() —
—![]() 的大小. (用反三角函数表示)
的大小. (用反三角函数表示)
21. (本小题满分14分)
已知函数![]() 直线l :
直线l :![]() .
.
(1) 求证:直线l与函数![]() 的图像不相切;
的图像不相切;
(2) 若当![]() 时,函数
时,函数![]() 的图像在直线l的下方,求c的范围.
的图像在直线l的下方,求c的范围.
22. (本小题满分14分)
已知函数![]() 数列
数列![]() 中,
中,![]()
![]() . 当a取不同的值时,得到不同的数列
. 当a取不同的值时,得到不同的数列![]() ,如当
,如当![]() 时,得到无穷数列
时,得到无穷数列![]() 当
当![]() 时,得到有穷数列
时,得到有穷数列![]() (1) 求a的值,使得
(1) 求a的值,使得![]() ;
;
(2) 设数列![]() 满足
满足![]()
求证:不论a取![]() 中的任何数,都可以得到一个有穷数列
中的任何数,都可以得到一个有穷数列![]() ;
;
(3) 求a的取值范围,使得当![]() 时,都有
时,都有![]() .
.
23. (本小题满分14分)
(1) 已知抛物线![]() 过焦点
过焦点![]() 的动直线l交抛物线于
的动直线l交抛物线于![]() 两点,
两点,![]() 为坐标原点,求证:
为坐标原点,求证:![]() 为定值;
为定值;
(2) 由 (1) 可知:过抛物线的焦点![]() 的动直线 l 交抛物线于
的动直线 l 交抛物线于![]() 两点,存在定点
两点,存在定点![]() ,使得
,使得
![]() 为定值. 请写出关于椭圆的类似结论,并给出证明.
为定值. 请写出关于椭圆的类似结论,并给出证明.
高三数学训练卷(一)参考答案
一、选择题(每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | B | A | D | C | B | C | C | A | D | C | B |
二、填空题(每小题4分,共24分)
13.![]()
14. 23 ;
15.![]()
16. 11 ;
17. ![]()
18. ![]()
三、解答题(共66分)
19.(本小题满分12分)
解:(1) 记该学生在第![]() 个交通岗遇到红灯
个交通岗遇到红灯![]()
![]() ,
,
![]()
答:该学生在第三个交通岗第一遇到红灯的概率为![]() ……………6分
……………6分
(2) 该学生至多遇到一次红灯指没有遇到红灯(记为A)或恰好遇到一次红灯(记为B)
![]() ……………7分
……………7分
![]()
![]() …………………9分
…………………9分
![]()
![]() ……………11分
……………11分
又![]() 所以p的取值范围是
所以p的取值范围是![]() ……………12分
……………12分
20.(本小题满分12分)
解:(1) 正方体中,![]() ,
,![]() 与
与![]() 所成的角为
所成的角为![]() 或其补角.
或其补角.
![]() ,
,![]() 和
和![]() 所成的角为
所成的角为![]() ……………4分
……………4分
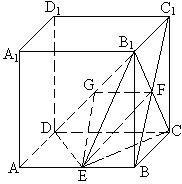
(2) 取![]() 的中点
的中点![]()
![]() 的中点
的中点![]() 连结
连结![]()
![]() 平面
平面![]() ,
,![]() .
.
又![]() ,
,![]()
![]() 平面
平面![]() .……………6分
.……………6分
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,![]()
![]() 平面
平面![]() ……………7分
……………7分
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() ……………8分
……………8分
(3) 连结![]() .
. ![]() 又
又![]() 平面
平面![]() ,
,
![]()
![]() 为二面角
为二面角![]() —
—![]() —
—![]() 的平面角. …………10分
的平面角. …………10分
设正方形的边长为a,则在![]() 中,
中,![]()
![]() ……………11分
……………11分
![]() 二面角
二面角![]() —
—![]() —
—![]() 的大小为
的大小为![]() …………12分
…………12分
21.(本小题满分14分)
解:(1) 证明:![]() ……………2分
……………2分
假设直线l :![]() 与函数
与函数![]() 的图像相切,则
的图像相切,则![]() 有实数解,即
有实数解,即![]() 有实数解. ……………5分
有实数解. ……………5分
因为![]() 时,方程
时,方程![]() 无实数解,所以直线l与函数
无实数解,所以直线l与函数![]() 的图像不相切.……………7分
的图像不相切.……………7分
(2) 当![]() 时,函数
时,函数![]() 的图像在直线l的下方,
的图像在直线l的下方,
即![]() 对于一切
对于一切![]() 都成立,……………9分
都成立,……………9分
即![]() 对于一切
对于一切![]() 都成立. ……………10分
都成立. ……………10分
令![]()
![]() 因为
因为![]()
所以![]() 在
在![]() 上单调递减,……………12分
上单调递减,……………12分
所以当![]() 时,
时,![]() ……………13分
……………13分
所以![]() ,所以c的范围是
,所以c的范围是![]() ……………14分
……………14分
22.(本小题满分14分)
解:(1) 因为![]()
![]()
所以![]()
![]() ……………2分
……………2分
要![]() 即要
即要![]() . 所以,
. 所以,![]() 时,
时,![]() ……………4分
……………4分
(2)由题知![]()
![]() 不妨设a取
不妨设a取![]() ,
,
所以![]()
![]() ……………6分
……………6分
……,
![]() 所以
所以![]() ……………8分
……………8分
所以不论a取![]() 中的任何数,都可以得到一个有穷数列
中的任何数,都可以得到一个有穷数列![]() .……………9分
.……………9分
(3) ![]() ……………11分
……………11分
因为![]()
![]()
![]() ,所以只要有
,所以只要有![]() 就有
就有![]() ……………12分
……………12分
由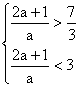 ,解得:
,解得: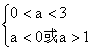 ,即
,即![]() .
.
所以,a的取值范围是![]() .……………14分
.……………14分
23.(本小题满分14分)
解:(1) 若直线l垂直于x轴,则![]() ,
,![]() .
.
![]()
![]() ……………2分
……………2分
若直线l不垂直于轴,设其方程为![]() ,
,![]()
![]() .
.
由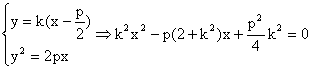
![]() ……………4分
……………4分
![]()
![]()
![]()
![]()
![]()
![]() .
.
综上,![]()
![]() 为定值. ……………6分
为定值. ……………6分
(2) 关于椭圆有类似的结论:过椭圆![]() 的一个焦点
的一个焦点![]() 的动直线l交椭圆于
的动直线l交椭圆于![]() 、
、![]() 两点,存在定点
两点,存在定点![]() ,使
,使![]() 为定值. ……………7分
为定值. ……………7分
证明:不妨设直线l过椭圆![]() 的右焦点
的右焦点![]()
![]() 其中
其中![]()
![]()
若直线l不垂直于轴,则设其方程为:![]() ,
,![]()
![]() .
.
由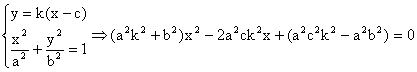 得:
得:
所以![]()
![]() ……………9分
……………9分
由对称性可知,设点![]() 在x轴上,其坐标为
在x轴上,其坐标为![]()
所以![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
要使![]() 为定值,
为定值,
只要![]()
即![]()
此时![]()
![]()
![]()
![]() ……………12分
……………12分
若直线l垂直于x轴,则其方程为![]() ,
,![]() ,
,![]() .
.
取点![]()
有![]()
![]()
![]()
![]() ……………13分
……………13分
综上,过焦点![]() 的任意直线l交椭圆于
的任意直线l交椭圆于![]() 、
、![]() 两点,存在定点
两点,存在定点![]()
使![]()
![]() 为定值. ……………14分
为定值. ……………14分