高三数学月考试卷
总分１５０分
一．选择题：本大题有10小题，每小题5分，共50分．
1．设全集U = R ，A =
，则
UA=（▲）
（A）
（B）
≥0
（C）｛x x≥0｝ （D）｛x x > 0｝
2．（理）若复数
为纯虚数，则（▲）
（A）
或
（B）且 （C）
（D）或
（文）“
”是“
”的（▲）
（A）充分不必要条件 （B）必要不充分条件
（C）充要条件 （D）既不充分又不必要条件
3．已知
在点P处的切线与直线y=4x-1平行，则切点P的坐标是（▲）
(A) (1,0) (B) (2,8) (C) (1,0)或(-1,-4) (D) (2,8)或(-1,-4）
4．设
为互不重合的平面，l,m,n为互不重合的直线，给出下列四个命题：
①若
则
∥
；②若
∥
∥
，则∥；
③若∥
则
∥； ④若
∥
则m∥n.
其中真命题的个数是（▲）
（A）1 （B）2 （C）3 （D）4
5．（理）已知随机变量
，若
，则
分别是（▲）
(A) 6和2.4 (B) 2和2.4 （C）2和5.6 (D) 6和5.6
（文）在数列
中，
，若其前n项和Sn=9，则项数n为（▲）
(A) 9 (B) 10 （C）99 (D) 100
6．（理）函数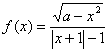
为奇函数的充要条件是（▲）
（A）
（B）
（C）
（D）
（文）已知
，则有（▲）
（A）
（B）
(C) 
(D) 
7．（理）函数
在区间
上至少取得2个最大值，则正整数t的最小值是（▲）
（A）9 （B）10 (C) 11 (D) 12
（文）函数
在区间上至少取得2个最大值，则正整数t的最小值是（▲）
（A）10 （B）9 (C) 8 (D)7
8．如果函数
的反函数是
，则下列等式中正确的是 （ ）
（A）
（B）
（C）
（D）
9．已知双曲线
的右顶点为
，而
是双曲线同一支上的两点，如果
是正三角形，则（▲）
（A）
（B）
（C）
（D）
10．（理）已知非零向量
，
满足＋＝－，则
的取值范围是（▲）
（A）
(B)
(C)
(D) 
（文）已知在同一平面上的三个单位向量
，它们相互之间的夹角均为120o，且
，则实数k的取值范围是（▲）
（A）k<0 (B) k>2 (C) k<0或k>2 (D) 0<k<2
二．填空题：本大题有4小题，每小题4分，共16分．
11．若
，则
▲ ．
12．(理)在
的展开式中含x2项的系数为
，则
= ▲ ．
（文）若
展开式中x3的系数为－80，则实数a= ▲ ．
13．经过空间内一定点P的直线中，与长方体ABCD—A1B1C1 D1的12条棱所在直线成等角的直线共有 ▲ 条
14．(理)符合条件：
的集合A、B、C的不同的组合个数共有 ▲ 个.
（文）已知集合A、B都是集合
的子集，且
，则符合条件的集合A、B的不同的组合个数共有 ▲ 个.
三．解答题：本大题有6小题，每小题14分，共84分．
15．(本小题满分14分)
已知角α、β满足：5sinα＋5cosα＝8，且α∈(0，)，β∈(，)，求cos(α＋β)的值.
15．∵5sinα＋5cosα＝8，∴sin(α＋)＝． …………3分
∵α∈(0，)，∴α＋∈(，)，∴cos(α＋)＝．…………5分
又∵，…………8分
∵β∈(，)，∴β＋∈(，)，∴cos(β＋)＝－，…………10分
∴sin[(α＋)＋(β＋)]＝sin(α＋)cos(β＋)＋cos(α＋)sin(β＋)＝－，………12分
∴cos(α＋β)＝－．…………14分
16．(本小题满分14分)
（理科做）二次函数
满足
，且
.
⑴求的解析式；
⑵在区间
上，
的图象恒在直线
的上方，求实数m的取值范围．
16．解：⑴令x=0，则f(1)－f(0)=0，∴f(1)=f(0)=1，
∴二次函数图象的对称轴为x=
，
∴可令二次函数的解析式为y=
a (x-)2+h ………………………4分
由f(0)=1，又可知f(-1)=3得a=1，h=
∴二次函数的解析式为y=f(x)=(x-)2+=x2-x+1 ………………7分
⑵∵ x2-x+1 >2x+m在[-1，l]上恒成立，
∴ x2-3x+1>m在[-l，1]上恒成立． ………………………………9分
令g(x)= x2-3x+1，∴y=g(x)在[-1，1]上单调递减，………………………12分
∴ g(x)min=g(1)= -l，∴m<-1． …………………………………………14分
（文科做）已知等差数列
的公差为
，等比数列
的公比为
，
，
，
.
⑴求数列与的通项公式；
⑵若对于一切正整数
，都有
成立，求常数
和
的值.
16．⑴由条件：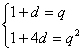
……3分 
. ……7分
⑵假设存在
使成立，则
即
对一切正整数恒成立.
……10分
∴
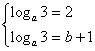……12分
又a > 0，可得：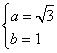
. ……14分
17．（本小题满分14分）
（理科做）A有一只放有x个红球，y个白球，z个黄球的箱子（x,y,z≥0，且
），B有一只放有3个红球，2个白球，1个黄球的箱子，两人各自从自己的箱子中任取一球比颜色，规定同色时为A胜，异色时为B胜 
⑴用x, y，z表示B胜的概率；
⑵当A如何调整箱子中球时，才能使自己获胜的概率最大？
（理科）⑴显然A胜与B胜为对立事件，A胜分为三个基本事件：
①A1：“A B均取红球”；②A2：“A B均取白球”；③A3：“A B均取黄球”
………7分
⑵由（1）知
，
于是
，即A在箱中只放6个红球时，获胜概率最大，其值为
……14分
（文科做）同时抛掷15枚均匀的硬币一次.
⑴试求至多有1枚正面向上的概率；
⑵试问出现正面向上为奇数枚的概率与出现正面向上为偶数枚的概率是否相等?请说明理由.
（文科）⑴记至多有一枚正面向上的概率为P1，则有
P1==
+
=
……（5分）
⑵记正面向上为奇数枚的概率为P2，正面向上为偶数枚的概率为P3，则有
P2=
+
+…+
=
+…+
)–
……（10分）
又事件“出现正面向上为奇数枚”与“出现正面向上为偶数枚”是对立事件， P3=1–
=，
出现正面向上为奇数枚的概率与出现正面向上为偶数枚的概率相等. ……（14分）
18.（本小题满分14分）
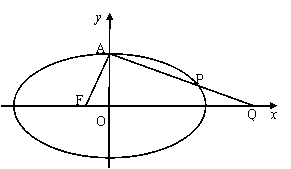设椭圆C：
的左焦点为F，上顶点为A，过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q，且
.
⑴求椭圆C的离心率；
⑵若过A、Q、F三点的圆恰好与直线l：
相切，求椭圆C的方程.
18．解⑴设Q（x0，0），由F（-c，0）
A（0，b）知
…2分
设
，得
…4分
因为点P在椭圆上，所以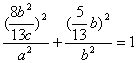
…………6分
整理得2b2=3ac，即2(a2－c2)=3ac，
,故椭圆的离心率e=………8分
⑵由⑴知
，于是F（－a，0） Q
，
△AQF的外接圆圆心为（a，0）半径r=FQ=a…………11分
所以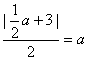
，解得a=2，∴c=1，b=
，所求椭圆方程为
…（14分）
19．（本小题满分14分）
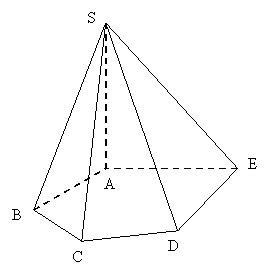
如图，在五棱锥S－ABCDE中，SA⊥底面ABCDE，
SA=AB=AE=2,BC=DE=
,∠BAE=∠BCD=∠CDE=120°.
⑴求异面直线CD与SB所成的角；
⑵证明：BC⊥平面SAB；
⑶用反三角函数值表示二面角B-SC-D的大小（本小问不必写出解答过程）.
20．（本小题满分14分）
（理科做）由原点O向曲线C:
(a≠0)引切线,切点
不同于点O ,再由P1引曲线C的切线，切于不同于P1的点
，如此继续作下去，……，得到点列
.⑴求
； ⑵求
与
的关系； ⑶若
,试比较与
的大小.
解(1) y′=3x2－6ax＋b.
过点P1(x1, y1)的切线l1的方程是
………4分
(2)过点Pn+1(xn+1,yn+1)的切线ln+1的方程是
由ln+1过曲线C上点P n(x n, yn)知
∵x n－xn+1≠0, ∴
同除以x n－xn+1得x n＋2xn+1－3a=0. …9分
(3) 由(2)得
故数列{x n－a}是以x 1－a=为首项,公比为－的等比数列,
∵a>0,∴当n为正偶数时, 
当n为正奇数时, 
……14分
（文科做）已知
，
.
⑴若
，且
，且方程
两实根的平方和为10，函数
的图象过点
,求函数的解析式.
⑵若
，
在
上最大值为2，最小值为
，证明：
且
.
20．解 ⑴∵，∴函数的对称轴为
，……①
∵函数图象过点，所以
， ……②
设方程的两根为
，则
＝
…③
由①②③得
，∴函数的解析式为
----6分
⑵由
得
，
，假设或
．
①由，得
，依题设可知
，因而函数在上是单调函数，，的最大值为
，最小值为
，于是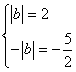
，由此得到矛盾，故．
②由得
，故函数在上单调，其最大值为，最小值为，由①知，这是不可能的，
综合①②可知，假设不成立，故且．---14分