高三数学周练12
一、选择题:本大题共4小题
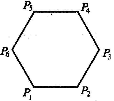 1.27.如图, 已知正六边形
1.27.如图, 已知正六边形![]() ,下列向量的数量积中最大的是(A )
,下列向量的数量积中最大的是(A )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2 (理).已知定义域为R的函数f(x)满足![]() ,且当x>2时,
,且当x>2时,
f(x)单调递增,如果![]() (A)
(A)
A.恒小于0 B.恒大于0 C.可能为0 D.可正可负
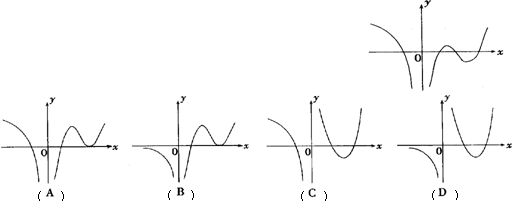 2.(文) 设函数f(x)在定义域内可导,y= f(x)的图象如右图所示,
2.(文) 设函数f(x)在定义域内可导,y= f(x)的图象如右图所示,
则导函数y= f′(x)的图象可能为 ( D )

3.若不等式![]() 对任意正整数n恒成立,则实数a的取值范围是(C)A.
对任意正整数n恒成立,则实数a的取值范围是(C)A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4(理).某学生对函数![]() 进行研究,得出如下四个结论:①函数
进行研究,得出如下四个结论:①函数![]() 在
在![]() 上单调递增;②存在常数
上单调递增;②存在常数![]() ,使
,使![]() 对一切实数
对一切实数![]() 均成立;③函数
均成立;③函数![]() 在
在![]() 无最小值,但一定有最大值;④点
无最小值,但一定有最大值;④点![]() 是函数
是函数![]() 图象的一个对称中心。其中正确的是
( B )
图象的一个对称中心。其中正确的是
( B )
A.①③ B.②③ C. ②④ D. ①②④
4(文).已知函数![]() 图象上,相邻的一个最大值点与一个最小值点恰好都在圆
图象上,相邻的一个最大值点与一个最小值点恰好都在圆![]() 上,则
上,则![]() 的最小正周期为 ( D )
的最小正周期为 ( D )
A.1 B.2 C.3 D.4
二、填空题
5.对于定义在R上的函数![]() ,若存在实数x0满足
,若存在实数x0满足![]() = x0,则称x0为函数
= x0,则称x0为函数![]() 的一个不动点.若二次函数
的一个不动点.若二次函数![]() =
=![]() 在其定义域R上至多有一个不动点,则实数a的取值范围是 ▲ .
在其定义域R上至多有一个不动点,则实数a的取值范围是 ▲ .
5.![]() .
.
![]() 6.已知
.我们把使乘积a1·a2·a3·…·an为整数的数n叫做“劣数”,则在区间(1,2004)内的所有劣数的和为
.
6.已知
.我们把使乘积a1·a2·a3·…·an为整数的数n叫做“劣数”,则在区间(1,2004)内的所有劣数的和为
.
6.∵![]() n+2=2k,由n=2k-2∈(1,2004)有2≤k≤10(k∈Z).故所有劣数的和为(22+23+……+210)-2×9=
n+2=2k,由n=2k-2∈(1,2004)有2≤k≤10(k∈Z).故所有劣数的和为(22+23+……+210)-2×9=![]() -18=2026.
-18=2026.
三、解答题
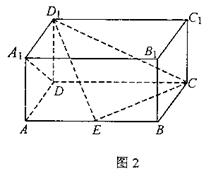
7.如图2,在长方体![]() ,点E在棱AB上移动,小蚂蚁从点A沿长方体的表面爬到点C1,所爬的最短路程为
,点E在棱AB上移动,小蚂蚁从点A沿长方体的表面爬到点C1,所爬的最短路程为![]() 。
。
(1)求证:D1E⊥A1D;
(2)求AB的长度;
|
7.解一:
(1)证明:连结AD1,由长方体的性质可知:
AE⊥平面AD1,∴AD1是ED1在
平面AD1内的射影。又∵AD=AA1=1,
∴AD1⊥A1D
|
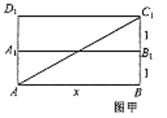
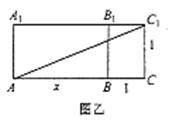
(2)设AB=x,∵四边形ADD1A是正方形,
∴小蚂蚁从点A沿长方体的表面爬到
点C1可能有两种途径,
如图甲的最短路程为![]()
|
![]()
![]()
![]() ………………9分
………………9分
(3)假设存在连结DE,设EB=y,过点D在平面ABCD内作DH⊥EC,连结D1H,则∠D1HD为二面角![]() 的平面角,
的平面角,
![]() ……………………………………11分
……………………………………11分
![]()
即![]()
![]()
![]()
|
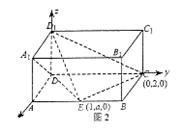
(1)如图建立空间坐标系设
AE=a
则E(1,a,0), D1(0,0,1)],A1(1,0,1)
![]()
![]() ………………………4分
………………………4分
(2)同解法一
(3)假设存在,平面DEC的法向量![]()
![]()
设平面D1EC的法向量![]() ,则
,则
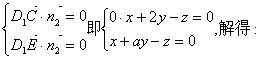
![]()
![]() ……………………………………12分
……………………………………12分
由题意得: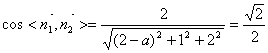
解得:![]() (舍去)
(舍去)
![]() ………………14分
………………14分
8 .(理).已知![]() 数列
数列![]() 满足下列条件:
满足下列条件:![]() ,
, ![]() ,
,![]()
![]() ( 1 )求
( 1 )求![]() 的解析式;
的解析式;
(2)求![]() 的通项公式;(3)试比较
的通项公式;(3)试比较![]() 与
与![]() 的大小,并加以证明.
的大小,并加以证明.
8.解:(1)![]()
![]() ①
① ![]()
![]() ②
②
由①②可得,![]()
(2)![]()
![]() ,两式相减得
,两式相减得![]() ,
,
即![]() ,则有
,则有![]() 且
且![]()
![]() ,
, ![]() ,则
,则![]() .
.
(3)![]()
![]() ① 又
① 又![]() ②
②
由①②可得,![]()
![]()
8.(文) 设数列![]() 是首项为6,公差为1的等差数列;
是首项为6,公差为1的等差数列;![]() 为数列
为数列![]() 的前
的前![]() 项和,且
项和,且![]()
(1)求![]() 及
及![]() 的通项公式
的通项公式![]() 和
和![]() ;
;
(2)若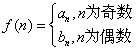 ,问是否存在
,问是否存在![]() 使
使![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
8.解:
(1)![]() 1分
1分
又当![]() 时,
时,![]()
当![]() 时,
时,![]()
上式对![]() 也成立,
也成立,
∴![]() ,
,
总之,![]() 4分
4分
(2)由已知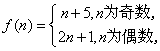 ∴当
∴当![]() 为奇数时,
为奇数时,![]() 为偶数,
为偶数,
由![]() ,得
,得![]() ,
,
∴![]() (舍去)
6分
(舍去)
6分
当![]() 为偶数时,
为偶数时,![]() 为奇数,
为奇数,
由![]() ,得
,得![]() ,
,
即![]() ,∴
,∴![]() 适合题意。
适合题意。
总之,存在整数![]() ,使结论成立 8分
,使结论成立 8分
9.(理)
已知函数f(x)=x2−alnx在(1,2![]() 是增函数,g(x)=x−a
是增函数,g(x)=x−a![]() 在(0,1)为减函数.
在(0,1)为减函数.
(Ⅰ)求f(x)、g(x)的表达式;
(Ⅱ)求证:当x>0时,方程f(x)=g(x)+2有唯一解;
(Ⅲ)当b>−1时,若f(x)≥2bx−![]() 在x∈(0,1
在x∈(0,1![]() 内恒成立,求b的取值范围.
内恒成立,求b的取值范围.
9.解:(Ⅰ)f/(x)=2x−![]() …………1分
…………1分
依题意f/(x)≥0在x∈(1,2]上恒成立,
∴ a≤2x2,
∴ a≤2. …………2分
又g/(x)=1−![]() , …………3分
, …………3分
依题意g/(x)<0在x∈(0,1)上恒成立,
∴ a>2![]() ,
,
∴ a≥2. …………4分
∴ a=2
∴f(x)=x2−2lnx,g(x)=x−2![]() …………5分
…………5分
(Ⅱ)由(Ⅰ)可知,方程为x2−2lnx
= x−2![]() +2,即x2−2lnx− x+2
+2,即x2−2lnx− x+2![]() −2=0.
−2=0.
设h(x)= x2−2lnx− x+2![]() −2,
−2,
由h/(x)=2x−![]() −1+
−1+![]() , …………6分
, …………6分
令h/(x)>0,
∵x>0,∴(![]() −1)(2x
−1)(2x![]() +2x+
+2x+![]() +2)>0,
+2)>0,
解得 x>1. …………7分
令h/(x)<0,
∵ x>0,∴(![]() −1)(2x
−1)(2x![]() +2x+
+2x+![]() +2)<0,
+2)<0,
解得 0<x<1. …………8分
由
| x | (0,1) | 1 | (1,+∞) |
| h/(x) | − | 0 | + |
| h(x) | 递减 | 0 | 递增 |
即h(x)在x=1处有一个最小值0,即当x>0且x≠1时,h(x)>0,∴h(x)=0只有一个解.
所以当x>0时,方程f(x)=g(x)+2有唯一解. …………9分
(Ⅲ)∵f/(x)=2x−![]() =
=![]() ,
,
∴当x∈(0,1]时f(x)为减函数,其最小值为1. …………11分
令y=2bx−![]() ,则y/=2b+
,则y/=2b+![]() .
.
∵b>−1,x∈(0,1],∴y/>0在(0,1]恒成立.
∴函数y=2bx−![]() 在x∈(0,1]为增函数,其最大值为2b−1. …………13分
在x∈(0,1]为增函数,其最大值为2b−1. …………13分
依题意![]() ,解得−1<b≤1为所求范围. …………14分
,解得−1<b≤1为所求范围. …………14分
9.(文)
已知函数![]() 在区间[0,1]上单调递增,在区间[1,2]上单调递减.
在区间[0,1]上单调递增,在区间[1,2]上单调递减.
(1)求a的值;
(2)设![]() ,若方程
,若方程![]() 的解集恰好有3个元素,求
的解集恰好有3个元素,求![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,是否存在实数对![]() ,使
,使![]() 为偶函数?如存在,求出
为偶函数?如存在,求出![]() 如不存在,说明理由.
如不存在,说明理由.
9.解:(1)![]() ,由已知
,由已知![]() 在
在![]() 上的值为正,
上的值为正,
在![]() 上的值为负.
上的值为负.
故![]() 是方程
是方程![]() 之根,
之根,
![]() . 3分
. 3分
(2)由![]() 有三个相异实根,
有三个相异实根,
故方程![]() 有两个相异的非零根.
有两个相异的非零根.
![]() 且
且![]() .
.
![]() . 7分
. 7分
(3)![]()
![]()
![]()
![]()
![]() 为偶函数, 10分
为偶函数, 10分
![]()
由(2)知![]() .
.
![]() .
.