高三数学周末测试
学号 姓名
一．选择题（每题5分，共40分）
1．双曲线
的渐近线方程是( )
(A) 
(B)
(C)
(D)
2．抛物线
上一点
的纵坐标为4，则点与抛物线焦点的距离为( )
(A) 2 (B) 3 (C) 4 (D) 5
3．“a=b”是“直线y=x+2与圆（x-a）2+（y-b）2=2相切”的 （ ）
A．充分不必要条件 B．必要不充分条件
C．充分必要条件 D．既不充分又不必要条件
4．圆(x+2)2+y2=5关于原点(0,0)对称的圆的方程 （ ）
(A) (x-2)2+y2=5； (B) x2+(y-2)2=5；
(C) (x+2)2+(y+2)2=5； (D) x2+(y+2)2=5。
5．从原点向圆 x2＋y2－12y＋27=0作两条切线，则该圆夹在两条切线间的劣弧长为( )
（A）π （B）2π （C）4π （D）6π
6．函数y＝ax2＋1的图象与直线y＝x相切，则a＝( )
(A)
(B)
(C) 
(D)1
7．若焦点在y轴上的椭圆
的离心率为
，则m=( )
（Ａ）
（Ｂ）
（Ｃ）
（Ｄ）
8．设椭圆的两个焦点分别为F1、、F2，过F2作椭圆长轴的垂线交椭圆于点P，若△F1PF2为等腰直角三角形，则椭圆的离心率是（ ）
（A）
（B）
（C）
（D）
二．填空题（共30分）
9．与双曲线
有共同的渐近线，并且经过点
的双曲线方程
10．已知直线ax＋by＋c＝0与圆O：x2＋y2＝1相交于A、B两点，且AB＝
，则
＝ .
11.设
的最小值是
12．若椭圆长轴长与短轴长之比为2，它的一个焦点是(2
,0),则椭圆的标准方程是
13．下面三题选做两个：
①已知a，b，c，d∈R+，且a+b+c+d=1，则a2+b2+c2+d2的最小值为
②已知直线的极坐标方程为
，则点（2，
）到该直线的距离为
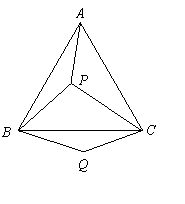③如图，
是等边三角形
内的一点，连结
，以
为边作
，且
，连结
．若
，连结
，则 
的形状
高三数学周末测试
答题卷 学号 姓名
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 |
9、 10、 11、 12、
13、① ② ③
三．解答题（共80分）
14．P为椭圆
上一点，
、
为左右焦点，若
（1） 求△
的面积；
（2） 求P点的坐标．（13分）
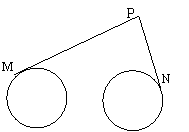15．（13分） 如图,圆O1与圆O2的半径都是1,O1O2=4,过动点P分别作圆O1、圆O2的切线PM、PN（M、N分别为切点），使得
试建立适当的坐标系，并求动点 P的轨迹方程.
16．已知直线L： x=-1-3t 与双曲线（y-2）2-x2=1相交于A、B两点，P点坐标为
y=2+4t
P（-1，2），求（1）PA·PB的值； （2）弦长AB； （3）弦AB中点M与点P的距离。（13分）
17．在△ABC中，角A、B、C所对的边分别为a、b、c，且cosA=
（13分）
（1）求
的值；
（2）若a=
，求bc的最大值。
18．已知中心在原点的双曲线C的右焦点为(2,0)，右顶点为
。
(1) 求双曲线C的方程；
(2) 若直线l：
与双曲线C恒有两个不同的交点A和B，且
(其中O为原点)，求k的取值范围。 （14分）
19．椭圆C1：
=1(a>b>0)的左右顶点分别为A、B.点P双曲线C2：
=1在第一象限内的图象上一点，直线AP、BP与椭圆C1分别交于C、D点.若△ACD与△PCD的面积相等．
（1）求P点的坐标；
（2）能否使直线CD过椭圆C1的右焦点，若能，求出此时双曲线C2的离心率，若不能，请说明理由.（14分）
答案：C D A A B B C D
9、
10、
11、-3 12、
13、（1）1/4 （2）
（3）Rt△
14、（1）3 （2）
15、x2+y2-12x+3=0
16、（1）
（2）
（3）
17、（1）
（2）
18、（1）
（2）
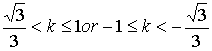
19．（14分）[解析]：（1）设P(x0,y0)(x0>0,y0>0)，又有点A(－a,0),B(a,0).
，
又
，
，
.
（2）
代入
，
∴CD垂直于x轴.若CD过椭圆C1的右焦点，则
故可使CD过椭圆C1的右焦点，此时C2的离心率为
.