高三数学周末练习
姓名
一、 选择题(本题共8小题,每小题5分,共40分)
1．已知集合
，则实数a的取值范围是（ ）
A．[1，2] B．（－1，2） C．[－1，2] D．（－2，1）
2.条件甲:“四边形ABCD是平行四边形”是条件乙:“
”成立的 ( )
A.充分不必要 B.必要不充分 C.充要条件 D.既不充分又不必要
3. 若
，则
=
( )
A.
B.
C.- 
D. 
4. 在数列
，则该数列中相邻两项的乘积是负数的是 （
）
A．
B．a22·a23 C．a23·a24 D．a24·a25
5.已知向量
,且
,则
=
( )
A.
B.
C.
D.
6．当a=3时，下面的程序段输出的结果是（ ）
IF a＜10 THEN
y=2*a
ELSE
y=a*a
PRINT y
A．9 B．３ Ｃ．１０ Ｄ．６
7.设直线
的方程为
,直线与
关于
对称,则直线经过点 ( )
A.(-1,3) B.(3,-1) C.(1,-3) D.(-3,1)
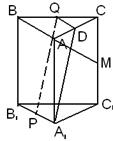8.在直三棱柱
中,
, 
,
、
分别为
的中点,
在
上,则直线
与直线
所成的角为 ( )
A.300 B.600 C.900 D.与
点的位置有关
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 |
|
|
|
|
|
|
|
|
二、填空题(本题共6题,每题5分,共30分)
9. 随机变量ξ的概率分布规律为
其中a是常数，则 
的值为
10. 10.抛物线
(
)上有一点M,它的横坐标是3,它到焦点的距离是5,则抛物线的方程为
11.一个球的内接长方体交于一点的三个面的面积分别为12,15,20,则这个球的表面积等于 .
12. 要使函数
上存在反函数，则a的取值范围是
13．下列三个题中选做两题：
①设a＞b＞c，且
恒成立，则m的取值范围是
②若实数x，y满足
，则u=y-3x的最大值是
③已知，⊙O中，直径CD交弦AB于E，E是的中点，CD = 16cm，
CE∶ED = 3∶1。则AB的长为
三、解答题(本题共6小题,共80分)
14. 编号为1，2，3的三位学生随意入坐编号为1，2，3的三个座位，每位学生坐一个座位。设与座位编号相同的个数为x．
（1）求随机变量x的概率分布；
(2）求随机变量x的数学期望和方差．
15.已知向量
),
令
,求
的最大值、最小正周期,并求在 [0,
]上的单调性
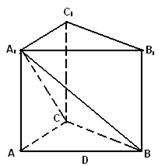16.直三棱柱
中,底面为等腰直角三角形,
, 
,连
为
的中点 (i)证明:
平面
(ii)求平面
与平面
所成二面角的正切值
17.已知函数
, 
).(i)当
时,求函数 的最小值.
(ii)若对任意的),> 0恒成立,试求
的取值范围.
18.已知函数
,数列{
}是公差为
的等差数列,{
}是公比为
的等比数列(
),
若
,
,
. (i)求{}、{}的通项公式
(ii)数列{
}是否为等差数列或等比数列?说明理由.
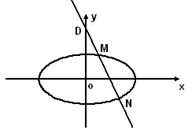
19．如图
△
中,
,
于
点,
,曲线E过C点,动点P在E上运动,且保持
的值不变. (i)建立适当的坐标系,求曲线E的方程
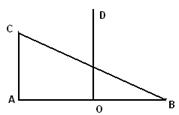(ii)过D点的直线
与曲线E相交于不同的两点
、
,且在D、
之间设
,求
的取值范围.,
高三数学周末练习答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | B | A | D | C | A | D | B | C |
二、填空题
9 , 
10,y2=8x 11 , 50
12, a≤1或a≥2 13、①m≤4 ②13 ③
三、解答题
14. （1）P(x＝0)＝＝，P(x＝1)＝＝， P(x＝2)＝0，P(x＝3)＝＝
| x | 0 | 1 | 2 | 3 |
| P | 0 |
∴概率分布为：
（2）Ex＝1×+3×＝1
Dx＝(1－0)2×+(1－1)2×+(1－2)2×0+(3－1)2×＝1
15.
+
=
= 
所以的最大值为
,最小正周期为
, 在[0,
]上单调递增,
16. (i)等腰直角三角形
中,
为斜边 的中线,
直三棱柱 面面
, 且面
面=
平面
(ii)作
,连
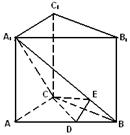
, 平面
故
为所求二面角的平面角
又
17.(i) 当时,
,因为在)上
所以,
,故
(ii)),> 0 恒成立
设
=
=
在)上单调递增,
的最小值为
即
时, > 0恒成了,故
18.(i)
,
4d-4
(ii)
,
数列{}既不是等差数列也不是等比数列
19. (i)如图建立坐标系 
动点的轨迹方程为椭圆 
故 曲线E的方程为
(ii) ①与
轴重合时
②与轴不重合时,
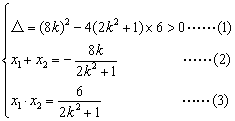设直线的方程为:
代入曲线E的方程中得
设
由(1)得
, 又
或
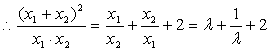
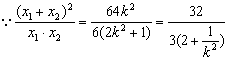又
, 
, 
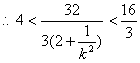
即: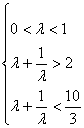
