高中数学复习综合训练
本试卷分选择题和非选择题两部分.满分150分.测试时间120分钟.
第一部分 选择题（共50分）
一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中, 只有一项是符合题目要求的．
（1）设全集U = {a，b，c，d，e}，集合A = {a，b，c，d}，B = {d , e}，则集合 A
B =（ ）.
（A）{d} （B）{ a ,b} （C）{b ,c ,d} （D）{a，b，c，d，e}
（2）2sin15°cos15° 的值等于（ ）.
（A） 0 （B） 
（C） 1 （D） 
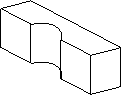
（3）实物图如图1 ，下列各选项中为实物图的俯视图的是（ ）. 图1
 |
（A） （B） （C） （D）
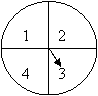
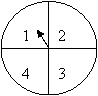（4）同时转动如图2所示的两个转盘，记转盘（甲）得
到的数为 
，转盘（乙）得到的数为 
， 则事
件
的概率为（ ）.
（A）
（B）
（C）
（D）
（甲） 图2 （乙）
（5）一个与球心距离为1的平面截球所得的圆面面积为
，则球的表面积为 （ ）
（A）
（B）
（C）
（D）
（6）在
中，若
，AB = 5，BC = 7，则的面积S 为（ ）
（A）
（B）
（C）
（D）
（7） 已知圆 
，点
2，0
及点 
，若直线
与圆 
没有公共点，
则 
的取值范围是（ ）.
（A）
（B）
（C）
（D）
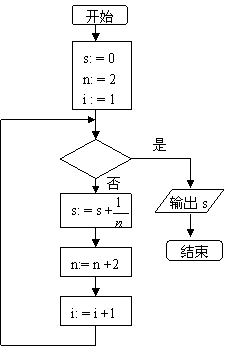（8）以下给出的是计算 
的值的一个
程序框图如图3 ，其中判断框内应填入的条件是（ ）.
（A）
（B）
（C）
（D）
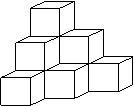
图4
图3
（9）将棱长相等的正方体按图4所示的形状摆放，从上往下依次为第1层，第2层，…… ，
则第20层正方体的个数是（ ）
（A） 420 （B） 440 （C） 210 （D） 220
（10）已知函数 
在区间 
2，2
上的最大值不大于2 ，
则函数 
的值域是（ ）
（A）
（B）
（C）
（D）
第二部分 非选择题（共100分）
二、填空题 ：本大题共4小题，每小题5分，共20分．
（11）已知
是首项
，公差
的等差数列，如果
，则序号
等于
（12）一个容量为20的样本，数据的分组及各组的频数如下表：(其中x，y∈N*)
| 分/组 | [10，20) | [20，30) | [30，40) | [40，50) | [50，60) | [60，70) |
| 频 数 | 2 | x | 3 | y | 2 | 4 |
则样本在区间 [10，50 ) 上的频率为 .
（13）非负实数
满足
则x + 3 y的最大值为 ，最小值为
（14）已知点 
在曲线 
上运动，作 
垂直于 轴于 
，则 
，
为坐标原点) 的周长的最小值为 .
三、解答题：本题共6小题，共80分．解答应写出文字说明、证明过程或演算步骤．
（15）（本题满分12分）
设向量 
向量
.
（16）（本题满分13分）
已知函数
，其中
.
（1）求函数
的最小正周期；
（2）求的递增区间.
（17）（本题满分13分）
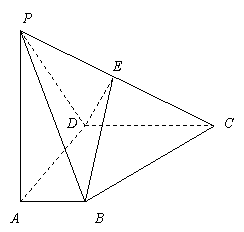
如图5所示 ，四棱锥P – ABCD的底面为一直角梯形，
BA⊥AD， CD⊥AD，CD = 2AB，
PA ⊥ 底面ABCD ，E为PC的中点 .
（1）证明：EB ∥ 平面PAD ；
（2）若PA = AD ，证明：BE ⊥平面PDC.
图5
（18）（本题满分14分）
设O为坐标原点，曲线x2 + y2 +2x－6y + 1 = 0上有两点P、Q
，满足关于直线x + my + 4 = 0对称，又满足
·
= 0 .
（1）求m的值； （2）求直线PQ的方程.
（19）（本题满分14分）
已知等比数列
共有m项 ( m ≥ 3 )，且各项均为正数，
= 1，+
+
= 7.
（1）求数列的通项
；
（2）若数列
是等差数列，且b1 = 1，bm = m，判断数列前m项的和
与数列
的前m项和Tm的大小并加以证明.
（20）（本题满分14分）
设
，(a＞b＞c), 且f (1) = 0 , g (x) = ax
+ b .
（1）求证：函数y = f (x) 与y = g (x) 的图象有两个交点；
（2）设f (x) 与g (x) 的图象交点A、B在x轴上的射影为A1、B1，求｜A1B1｜的取值范围；
（3）求证：当x ≤ －
时，恒有f (x) ＞ g (x)
.