高中三年级数学期中考试试卷(理科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至2页，第Ⅱ卷3至8页。共150分。考试时间120分钟。
第Ⅰ卷(选择题，共60分)
注意事项：
1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考场号、座号、考试科目用铅笔涂写在答题卡上。
2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上。
3．考试结束，将第Ⅱ卷和答题卡一并交回。
一、选择题：本题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．已知集合A＝{a，1}，集合B＝{2，3a}，A∪B＝{1，2，9}，则A∩B＝
A．{1} B．{2} C．{4} D．Ø
2．若复数
∈R，则实数a的值是
A．1 B．－1 C．2 D．－2
3．
＝
A．2 B．1 C．－2 D．－1
4．函数f(x)＝
的反函数是f－1 (x))，若f－1 (x)＜0，则x的取值范围是
A．(－∞，－1) B．(－∞，0) C．(－1，1) D．(1，＋∞)
5．在△ABC中，已知A(－4，0)，B(4，0)，且sinA－sinB＝
sinC，则点C的轨迹方程是
A．
－
＝1 (x＞2)
B．
－
＝1 (x＞2)
C．－＝1 (x＜－2)
D．－＝1 (x＜－2)
6．从1，2，3，4，5这五个数字中，任取三个组成无重复数字的三位数(若三个数字中有
2和3，则2排在3的前面)，这样的三位数共有
A．9个 B．15个 C．45个 D．51个
7．不等式｜｜
｜－｜
｜｜≤｜±｜≤｜｜＋｜｜中两等号同时成立的充要条件是
A．｜｜·｜｜＝0
B．｜｜＋｜｜＝0
C．｜｜－｜｜＝0
D．·>0
8．已知点(3，1)和(－4，6)在直线3x－2y＋a＝0的两侧，则a的取值范围是
A．a＜－7或a＞24 B．a＝7或a＝24
C．－7＜a＜24 D．－24＜a＜7
9．二项式(x＋
)n的展开式中前三项系数成等差数列，则展开式的常数项为
A．T4＝
B．T4＝70
C．T5＝7
D．T5＝
10．在直三棱柱ABC—A1B1C1中，AC⊥BC，∠AB1C=a，∠ABC＝β，∠BAB1＝0，则
A．sina=sinβcosθ B．sinβ＝sinacosβ C．cosa=cosβcosθ D．cosβ＝cosacosθ
11．函数f(x)＝x＋4
的单调递增区间为(－∞，1]，则实数a等于
A．1 B．3 C．5 D．7
12．已知f(x)是定义在R上的奇函数，且满足f (x＋2)＝－f (x)，当0≤x≤1时，f(x)＝
x，则使f(x)＝－的x的值是
A．2k，k∈Z B．2k－1，k∈Z C．4k－1，k∈Z D．4k＋1，k∈Z
第Ⅱ卷(非选择题，共90分)
注意事项：
1．第Ⅱ卷共6页，用钢笔或圆珠笔直接写在试题卷上。
2．答卷前将密封线内的项目填写清楚。
二、填空题：本大题共4个小题，每小题5分，共20分．把答案填在题中横线上．
13．在一次有奖明信片的100000个有机会中奖的号码(编号00000—99999)中，邮政部门按照随机抽取的方式确定后两位是23的号码作为中奖号码，这是运用了____________抽样方法．
14．函数y＝log2｜x－a｜(a≠0)的图象关于直线x＝2成轴对称图形，则a＝____________．
15．内接于半径为R的球的圆柱体体积的最大值是____________________________.
16．给出下列四个命题：
①函数y＝f(x)在x＝x0处可导，则函数y＝f(x)在x0处连续；
②函数y＝f(x)在x＝x0处的导数f (x0)＝0，则f(x0)是函数y＝f(x)的一个极值；
③函数y＝f(x)在x＝x0处的导数不存在，则f(x0)不是函数y＝f(x)的一个极值；
④函数y＝f(x)在x＝x0处的导数不存在，则f(x0)不是函数y＝f(x)的最值．
其中正确的命题的序号是________________(请把所有正确命题的序号都填上)．
三、解答题：本大题6个小题，共70分．解答题应写出文字说明、证明过程和演算步骤．
17．(本小题满分10分)已知点A(4，0)，B(0，4)，C(3cosα，3sinα)．
(1)若α∈(－π，0)，且｜
｜＝｜
｜，求角α的值；
(2)若
·＝0，求
的值．
18．(本小题满分12分)
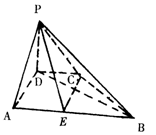在四棱锥P—ABCD中，PD⊥底面ABCD，AB∥CD，PD＝CD＝AD＝
AB，∠ADC
＝120°．
(1)求证：平面APD⊥平面PDB；
(2)若AB的中点为E，求二面角D—PC—E的大小．
19．(本小题满分12分)
已知椭圆的中心在原点，离心率为，一个焦点是F(－1，0)．
(1)求随圆的方程；
(2)设Q是椭圆上的一点，且过点F、Q的直线l与y轴交于点M，若｜
｜＝2｜
｜，求直线l的斜率．
20．(本小题满分12分)
甲、乙两人掷硬币，甲用一枚硬币掷3次，记正面朝上的次数为ξ；乙用这枚硬币掷2次，记正面朝上的次数为η．
(1)求Eξ和Dξ；
(2)规定：若ξ>η，则甲获胜；若ξ<η，则乙获胜，分别求出甲、乙获胜的概率．
21．(本小题满分12分)
已知数列｛an｝中a1＝
, an＝2－
(n≥2)，设bn＝
(1)求数列｛an｝的通项公式；
(2)记sn＝b1＋b2＋…＋bn，求 
．
22．(本小题满分12分)
设a∈R，函数f(x)＝(ax2－2x)e－x．
(1)当a≥0时，求f (x)的极值点；
(2)设f(x)在[－1，1]上是单调函数，求a的取值范围．
