三 角 函 数
一、知识要点：三角函数基本概念、三角函数的恒等变形(化简,求值,等式的证明)、三角函数的图象和性质
1、三角变换基本解题方法：切割化弦，异名化同名，异角化同角，高次化低次，无理化有理．
常用的技巧：升幂降幂法、辅助元素法，“1”的代换法、利用倍角公式建立2α与α、α与
的关系、角的配凑等
2、对三角函数性质的考查总是与三角变换相结合．一般解题规律是先对三角函数关系式进行三角变换，使之转化为一个角的三角函数的形式，再利用换元法转化为对基本三角函数性质的研究．
3、易错点：要注意正切函数定义域的限制；在三角变形过程中要注意自变量取值区间的变化，以防出现增根或失根；凡遇到参数或字母时，注意分情况进行讨论。
4、主要数学思想：化归思想、函数思想、数形结合思想、分类讨论思想
二、主干知识点、基本方法回顾练习：
1. 若
是第三象限的角，且
，那么
的值为（ C）
A. B. － C.
D. －
2. 已知函数
在［
，
］上单调递增，则实数
的取值范围是（ A ）
A．（0，
B．（0，2 C．（0，1 D．
3．先将
的图象沿
轴向右平移
个单位，再将图象上每一个点的横坐标伸长为原来的2倍，而保持它们的纵坐标不变，得到的曲线与
的图象相同，则的解析式是（ C ）
A．
B．
C．
D．
4．若
为第二象限的角，则下列各式恒小于0的是（ B ）
A．
B．
C．
D．
5．已知
，
，则
（ A
）
A、 2 B、 3 C、1 D、无法确定
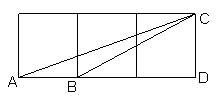6. 如图是由三个相同的正方形相接，在△ABC中，锐角∠ACB=，则
=（C ）
A．
B．
C．
D．
7．函数
相邻两条对称轴的距离为 （ C ）
A．2
B．
C．
D．
8. 函数
的递减区间是_____
_______，递增区间是______________，
9.函数
有一条对称轴为
，则
_5_______。
10．函数
的定义域为 
11．函数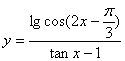
的定义域为
12．知
是方程
的二根，且
，则
13. 已知
(
),求值
2
14．弹簧挂着的小球作上下运动，它在时刻
秒相对于平衡位置
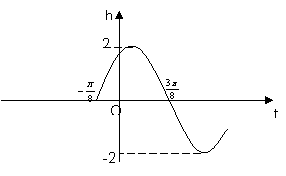（即静止时的位置）的高度
厘米满足函数
，
（ω＞0,｜
｜＜ 
＝（如右图），则小球运动的高度与时
间的关系式为
，小球的最高点与最低点到平衡位置的位移分别是
15．在下列四个命题中，①函数
的最小值是
。②函数
的最小正周期是
。③已知
，且
，则
的取值集合为
。④函数
的定义域是
。把你认为正确命题的序号填在指定的位置上 _______________.
16．求值
=
17．已知
则
=
18. 已知
.
（I）求sinx－cosx的值； （Ⅱ）求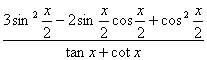
的值.
19.已知函数
的图象在y轴右侧的第一个最高点（函数取最大值的点）为P（
，2），在原点右侧与x轴的第一个交点为H（
，0）。
（1）求函数
的解析式； （2）求函数在区间［
］上的对称轴方程。
（3）求函数的单调递增区间
20．已知f（x）=2sin（x+
）cos（x+）+
cos2（x+）－
．
（1）试化简f（x）的解析式；
（2）若θ∈［0，π］，试求出使f（x）为偶函数时的θ的值；
（3）在（2）成立的条件下，求满足f（x）≤1且x∈［－π，π］的集合．