高三第三次月考数学试题（文科）
参考公式：
如果事件A、B互斥，那么 P(A+B)=P(A)+P(B)
如果事件A、B相互独立，那么 P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是P，那么n次独立重复试验中恰好发生k次的概率
球的体积公式
，球的表面积公式 
，其中R表示球的半径
一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的.
|
的定义域为集合A，函数
的定义域为集合B，则
B）=（ ）
A．[1，2] B．[1，2
C．
D．（1，2）
2．某公司共有1000名员工，下设若干部门，现采用分层抽样方法，从全体员工中抽取一个容量为80的样本，已知广告部被抽取了4个员工，则广告部的员工人数是 （ ）
A．30 B．40 C．50 D．60
3．设l、m为不同的直线，α、β为不同的平面，给出下列四个命题：
①若
l∥β，m∥β，则α∥β； ②若
则m⊥β；
③若a⊥β，l∥α，则l⊥β；
④若α∥β，
，则l∥m.
其中真命题的个数共有 （ ）
A．1个 B．2个 C．3个 D．4个
4．已知a=
，b=2，且（a+b）·a=0，则向量a与b的夹角为 （ ）
A．30° B．60° C．120° D．150°
| |
A．58种 B．50种 C．48种 D．40种
6．若不等式
成立的充分条件是
，则实数a的取值范围是 （ ）
A．
B．
C．
D．
7．已知函数
是奇函数，则函数
的图象关于下列哪个点成中心对称 （ ）
A．（1，0） B．（－1，0） C．（
，0） D．（－，0）
8．已知两定点A、B，且AB=4，动点P满足PA－PB=3，则PA的最小值是 （ ）
A．
B．
C．1 D．
9．在一次射击练习中，已知甲独立射击目标被击中的概率为
，甲和乙同时射击，目标没有被击中的概率为
，则乙独立射击目标被击中的概率是 （ ）
A．
B．
C．
D．
10．如果函数
在区间D上是“凸函数”，则对于区间D内任意的
，有
成立. 已知函数
在区间[0，π]上是“凸函数”，则在△ABC中，
的最大值是 （ ）
A． B．
C． D．
二、填空题：本大题共5小题，每小题4分，共20分.
11．已知
，则a与b的大小关系是
.
12．函数
的最小正周期是
.
13．若
的展开式中，只有第四项的系数最大，则这个展开式中的常数项的值是
.（用数字作答）
|
的两个焦点分别为F1、F2，点P在椭圆上，且
.
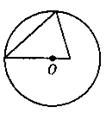
15．正三棱锥的四个顶点都在同一球面上，经过三棱锥的一条
侧棱和球心O的截面如右图，若球的表面积为12π，
则这个正三棱锥的底面边长为 .
三、解答题：本大题有6小题，共80分. 解答应写出文字说明，证明过程或演算步骤.
16．（本小题满分12分）
在△ABC中，角A、B、C、的对边分别为a、b、c，已知
（I）求角B的大小；
（II）若a、b、c成等比数列，试确定△ABC的形状.
17．（本小题满分12分）
已知甲、乙、丙三种食物的维生素A、B含量及成本如下表：
| 甲 | 乙 | 丙 | |
| 维生素A（单位/kg） | 600 | 700 | 400 |
| 维生素B（单位/kg） | 800 | 400 | 500 |
| 成本（元/kg） | 11 | 9 | 4 |
现在用甲、乙、丙三种食物配成100kg混合食物，并使混合食物内至少含有56000单位维生素A和63000单位维生素B，问：分别用甲、乙、丙三种食物各多少kg，才能使这100kg混合食物的成本最低？其最低成本为多少元？
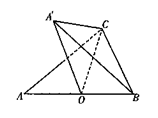18．（本小题满分14分）
| |
（I）若点A′到直线BC的距离为1，求二面角
A′—BC—A的大小；
（II）若∠A′CB+∠OCB=π，求BC边的长.
19．（本小题满分12分）
已知数列
为等差数列，其前n项和为
（I）若
成立，并将其整合为一个等式；
（II）一般地，若存在正整数k，使
，我们可将（I）中的结论作相应推广，试写出推广后的结论，并推断它是否正确.
20．（本小题满分14分）
设a为实常数，函数
（I）若函数
的图象在点P（1，
）处的切线的倾斜角为
，求函数的单调区间；
（II）若存在
，使
，求a的取值范围.
21．（本小题满分14分）
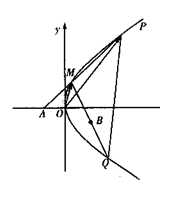已知点A（－1，0），B（1，－1）和抛物线.
，O为坐标原点，过点A的动直线l交抛物线C于M、P，直线MB交抛物线C于另一点Q，如图.
（I）若△POM的面积为
，求向量
与
的夹角；
（II）试探求点O到直线PQ的距离是否存在最大值？若存在，求出这个最大值；若不存在，说明理由.
高三年级三月月考
数学试题（文科）参考答案
一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的.
1—5：DCBDC 6—10：ACABD
二、填空题：本大题共5小题，每小题4分，共20分.
11．
12．
13．20 14．9 15．3
三、解答题： 本大题共6小题，共80分，解答应写出文字说明，证明过程或演算步骤.
16．解：（I）由已知及正弦定理，有
…………………………………………（4分）
……………（6分）
（II）由题设，
……（10分）
从而
为正三角形.……………………………………（12分）
17．解：设用甲种食物xkg，乙种食物ykg，丙种食物（100－x－y）kg，
混合食物的成本为z元. 则…………………………………………………………（2分）
…………（5分）
且
………………………………（6分）
当且仅当
时取等号，
…………………（9分）
答：分别用甲种食物50kg，乙种食物20kg，丙种食物30kg，才能使混合食物成本最低，其最低成本为850元.………………………………………………………………（12分）
18．解：（I）由已知，OC⊥OB，OC⊥OA′从而平面A′OB⊥平面ABC.
过点A′作A′D⊥AB，垂足为D，则A′D⊥平面ABC，……………………（2分）
∴∠A′ED=30°，又A′O=BO=1，∴∠A′OD=60°，
从而A′D=A′Osin60°=.……………………………………………………（4分）
过点D作DE⊥BC，垂足为E，连结A′E，据三垂线定理，A′E⊥BC.
∴∠A′ED为二面角A′—BC—A的平面角.……………………………………（5分）
由已知，A′E=1，在Rt△A′DE中
∴∠A′ED=60°故二面角A′—BC—A的大小为60°.…………………………（7分）
（II）设BC=
，∠A′CB=θ，则A′C=，∠OCB=π－θ.
在Rt△BOC中，
…………（9分）
|
在△A′BC中，A′B2=A′C2+BC2－2A′C·BC
…………（12分）
………………………（14分）
19．解：（I）
；……………（2分）
；…………………………（4分）
………………………………………………（5分）
∴对任意
…………………………………（7分）
（II）推广：设等差数列的前n项和为Sn，若存在正整数k，使
则对任意
…………………………（9分）
设的公差为
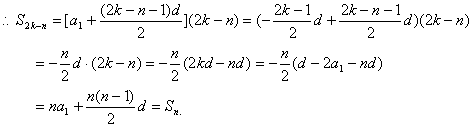
故推广后的结论正确.…………………………………………………………………（14分）
20．解：（I）
据题意，
………………………………（3分）
………………………………………………（4分）
故
；
故
的单调递增区间是[0，
]，单调递减区间是（－∞，0
，[，+∞.…（7分）
（II）
（1）若
上是减函数。
又
……………………………………（10分）
（2）若
从而在（0，
上单调递增，在[
，+
上单调递减.
据题意，
的取值范围是（3，+∞）.……（14分）
21．解：（I）设点
、M、A三点共线，
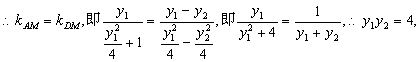………（2分）
…………………………………………………（3分）
设∠POM=α，则
由此可得tanα=1.……………………（5分）
又
……………………（6分）
（II）设点
、B、Q三点共线，
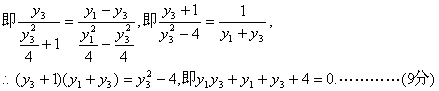
即
……………………………………（10分）
即
……………………（12分）
由（*）式，
代入上式，得
由此可知直线PQ过定点E（1，－4）.
故存在定一点E（1，－4），使
∥
…………………………………………（14分）